Comparing fractions is a fundamental skill in mathematics, essential for everyday life, from cooking and baking to understanding finances and measurements. At its core, comparing fractions means determining which of two or more fractions represents a larger or smaller part of a whole. While comparing fractions with the same denominator is straightforward, the task becomes more complex when denominators differ. This guide will delve into effective methods for Comparing Fractions With Different Denominators, ensuring you master this crucial mathematical concept.
Understanding the Basics: Numerators and Denominators
Before we dive into comparing fractions with different denominators, let’s briefly revisit what fractions are and the roles of their numerators and denominators. A fraction represents a part of a whole and is written as two numbers separated by a line.
- Numerator: The number on the top of the fraction bar. It tells you how many parts of the whole you have.
- Denominator: The number on the bottom of the fraction bar. It indicates the total number of equal parts the whole is divided into.
For instance, in the fraction 3/4, ‘3’ is the numerator, indicating we have 3 parts, and ‘4’ is the denominator, showing the whole is divided into 4 equal parts.
The Challenge of Different Denominators
Comparing fractions with the same denominator is simple. If the denominators are the same, you just compare the numerators. The fraction with the larger numerator is the larger fraction. For example, 3/7 is less than 5/7 because 5 is greater than 3, and both fractions are dividing the whole into the same number of parts (sevenths).
However, when denominators are different, we can’t directly compare the numerators. Consider comparing 1/2 and 2/3. Here, the denominators (2 and 3) are different. We can’t immediately tell which fraction is larger just by looking at the numerators (1 and 2). We need a method to make the comparison fair, and that usually involves finding a common denominator.
Method 1: Finding a Common Denominator (Least Common Multiple – LCM)
One of the most reliable methods for comparing fractions with different denominators is to find a common denominator. The most efficient common denominator to use is the Least Common Multiple (LCM) of the denominators. Here’s how it works:
Steps:
- Identify the denominators: Look at the denominators of the fractions you want to compare.
- Find the LCM of the denominators: Calculate the Least Common Multiple (LCM) of these denominators. The LCM is the smallest number that is a multiple of both denominators.
- Convert each fraction to an equivalent fraction with the LCM as the new denominator: For each fraction, determine what number you need to multiply the original denominator by to get the LCM. Then, multiply both the numerator and the denominator by that same number to create an equivalent fraction.
- Compare the numerators: Once both fractions have the same denominator (the LCM), compare their numerators. The fraction with the larger numerator is the larger fraction.
Example: Compare 1/2 and 2/5
- Denominators: 2 and 5
- LCM of 2 and 5: The LCM of 2 and 5 is 10 (since 10 is the smallest number divisible by both 2 and 5).
- Convert to equivalent fractions:
- For 1/2: To get a denominator of 10, multiply both numerator and denominator by 5: (1 × 5) / (2 × 5) = 5/10
- For 2/5: To get a denominator of 10, multiply both numerator and denominator by 2: (2 × 2) / (5 × 2) = 4/10
- Compare numerators: Now we compare 5/10 and 4/10. Since 5 > 4, then 5/10 > 4/10.
Conclusion: Therefore, 1/2 > 2/5.
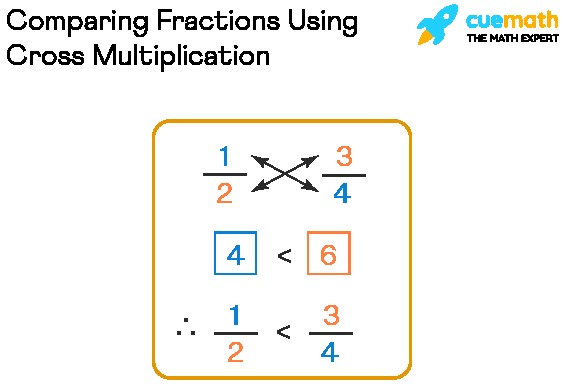
Method 2: Cross-Multiplication
Cross-multiplication is a quicker method for comparing two fractions, especially when you need a fast comparison and don’t necessarily need to find equivalent fractions.
Steps:
- Write the fractions side by side: Let’s say you are comparing a/b and c/d.
- Cross-multiply: Multiply the numerator of the first fraction (a) by the denominator of the second fraction (d), and multiply the numerator of the second fraction (c) by the denominator of the first fraction (b).
- Compare the products:
- If (a × d) > (c × b), then a/b > c/d.
- If (a × d) < (c × b), then a/b < c/d.
- If (a × d) = (c × b), then a/b = c/d.
Example: Compare 3/4 and 5/7
- Fractions: 3/4 and 5/7
- Cross-multiply:
- 3 × 7 = 21
- 5 × 4 = 20
- Compare products: Since 21 > 20, then 3/4 > 5/7.
Conclusion: Therefore, 3/4 > 5/7.
Method 3: Decimal Conversion
Another method to compare fractions is to convert them into decimal form. This is particularly useful when you are comfortable with decimal numbers or when dealing with calculators.
Steps:
- Convert each fraction to a decimal: Divide the numerator by the denominator for each fraction.
- Compare the decimal values: Compare the resulting decimal numbers. The fraction that converts to a larger decimal is the larger fraction.
Example: Compare 4/5 and 7/10
- Convert to decimals:
- 4/5 = 4 ÷ 5 = 0.8
- 7/10 = 7 ÷ 10 = 0.7
- Compare decimals: 0.8 > 0.7
Conclusion: Therefore, 4/5 > 7/10.
Method 4: Visual Comparison (Fraction Bars or Circles)
Visual models can be very helpful for understanding and comparing fractions, especially for visual learners. Fraction bars or circles can visually represent fractions, making it easier to see which fraction is larger.
How to Visualize:
- Represent each fraction with a visual model: Draw two identical rectangles or circles. Divide one into the number of parts indicated by the denominator of the first fraction and shade the number of parts indicated by the numerator. Do the same for the second fraction.
- Compare the shaded areas: By visually comparing the shaded areas, you can determine which fraction represents a larger portion of the whole.
Example: Compare 2/3 and 3/4
If you draw fraction bars for 2/3 and 3/4, you will visually see that the shaded area representing 3/4 is larger than the shaded area representing 2/3.
Conclusion: Therefore, 3/4 > 2/3.
Note: While visualization is excellent for understanding, it might not be precise for very close fractions or for formal mathematical comparisons.
When to Use Each Method
- Common Denominator (LCM): Best for a thorough understanding and when you need to perform further operations with the fractions. It’s a foundational method that reinforces the concept of equivalent fractions.
- Cross-Multiplication: Ideal for quick comparisons of two fractions, especially in tests or situations where time is limited. It’s efficient and less prone to errors for simple comparisons.
- Decimal Conversion: Useful when you are comfortable with decimals or when using calculators. It’s practical for comparing multiple fractions or when fractions are complex.
- Visual Comparison: Excellent for initial learning and for gaining an intuitive understanding of fraction size. Best for educational purposes and making concepts concrete.
Common Mistakes and How to Avoid Them
- Mistake: Directly comparing numerators when denominators are different.
- Avoid: Always check if denominators are the same first. If not, use one of the methods to make them comparable.
- Mistake: Incorrectly finding the LCM.
- Avoid: Practice finding LCMs. List multiples of each denominator and find the smallest common one, or use prime factorization method.
- Mistake: Making errors during cross-multiplication.
- Avoid: Double-check your multiplication and ensure you are comparing the products correctly against their corresponding fractions.
- Mistake: Rounding decimals prematurely when converting fractions.
- Avoid: If decimals are terminating, use all decimal places. If they are repeating, use enough decimal places for accurate comparison, or prefer LCM or cross-multiplication for exact comparisons.
Real-World Applications of Comparing Fractions with Different Denominators
Comparing fractions isn’t just a classroom exercise; it’s used in many real-life situations:
- Cooking and Baking: Recipes often involve fractions of ingredients. Comparing 1/3 cup to 1/4 cup is crucial for getting proportions right.
- Measurements in Construction and DIY: Comparing lengths like 5/8 inch and 3/4 inch is essential for accurate building and crafting.
- Financial Literacy: Comparing interest rates like 1/2% and 2/5% helps in making informed decisions about loans or investments.
- Time Management: Splitting tasks into fractional parts of an hour and comparing them helps in scheduling and prioritizing.
- Sports and Statistics: Comparing performance metrics often involves fractions, like comparing batting averages in baseball or success rates in other sports.
Conclusion
Mastering the comparison of fractions with different denominators is a vital step in building a strong foundation in mathematics. By understanding and practicing the methods outlined – finding a common denominator, cross-multiplication, decimal conversion, and visual comparison – you can confidently tackle any fraction comparison problem. Choose the method that best suits the situation and your comfort level. With practice, comparing fractions will become second nature, enhancing your mathematical skills and problem-solving abilities in various real-world contexts.
FAQs on Comparing Fractions with Different Denominators
What is the most straightforward method for comparing fractions with different denominators?
Cross-multiplication is often the quickest method for comparing two fractions. However, finding a common denominator (LCM) provides a deeper understanding and is useful when you need to perform further operations.
Can I always use decimal conversion to compare fractions?
Yes, you can always convert fractions to decimals to compare them. It’s a practical method, especially with a calculator. However, for exact comparisons and conceptual understanding, LCM or cross-multiplication might be preferable.
Is visual comparison accurate for all fractions?
Visual comparison is excellent for understanding the concept, but its accuracy is limited, especially for fractions that are very close in value or when precision is required.
Why do we need to find a common denominator when comparing fractions?
Finding a common denominator allows us to compare fractions by making the “wholes” divided into the same number of parts. Once the denominators are the same, we can directly compare the numerators to determine which fraction is larger or smaller.
What if I need to compare more than two fractions with different denominators?
Finding the LCM of all denominators and converting all fractions to have this common denominator is the most effective approach when comparing multiple fractions. Then you can compare all numerators at once.
Is comparing fractions with different denominators relevant in real life?
Absolutely. Comparing fractions with different denominators is highly relevant in many real-life situations, including cooking, measurements, finance, and more, wherever proportional comparisons are needed.
What if the numerators are also different when denominators are different?
When both numerators and denominators are different, you must use one of the comparison methods (LCM, cross-multiplication, or decimal conversion) to accurately determine which fraction is larger. Direct comparison is not possible without employing these methods.
How does understanding fraction comparison help in more advanced math?
Understanding fraction comparison is crucial for more advanced mathematical topics such as ratios, proportions, algebra, and calculus. It builds a foundational number sense necessary for complex mathematical operations and problem-solving.