When Comparing The Value Of Decimals The Correct Sequence Is

When Comparing The Value Of Decimals The Correct Sequence Is crucial for accurate comparisons, especially when dealing with finances, measurements, or scientific data. COMPARE.EDU.VN offers a comprehensive guide to master decimal comparison, ensuring precision and avoiding common pitfalls. Decimals, decimal numbers, and decimal places all play a key role. This guide provides a step-by-step approach to understanding place value, comparing fractions to decimals, and using number lines for visual representation, offering a complete understanding of decimal concepts and comparison techniques.

1. Understanding Decimal Comparison

Comparing decimals involves determining which decimal number has a greater or lesser value. This is essential in various real-life scenarios, from calculating expenses to understanding scientific measurements. The process requires a systematic approach to ensure accuracy.

1.1. The Significance of Place Value

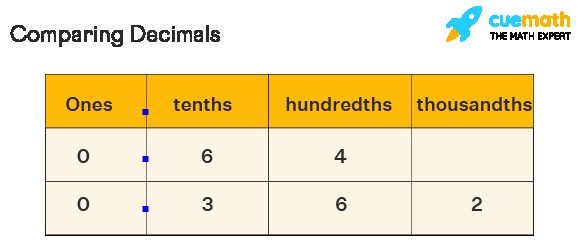
Place value is the cornerstone of decimal comparison. Each digit in a decimal number holds a specific value based on its position relative to the decimal point. Understanding these values is vital for accurate comparisons.

Ones Place: The digit immediately to the left of the decimal point represents whole units.
Tenths Place: The first digit to the right of the decimal point represents tenths (1/10).
Hundredths Place: The second digit to the right represents hundredths (1/100).
Thousandths Place: The third digit to the right represents thousandths (1/1000).

Understanding decimal place values is fundamental when comparing the value of decimals, as the position of each digit determines its contribution to the overall magnitude.

1.2. Basic Rules for Comparing Decimals

To compare decimals effectively, follow these basic rules:

Align the Decimal Points: Ensure that the decimal points of the numbers being compared are aligned vertically. This makes it easier to compare digits in the same place value.
Compare Whole Numbers: Start by comparing the whole number parts (the digits to the left of the decimal point). The decimal with the larger whole number is greater.
Compare Tenths Place: If the whole numbers are equal, compare the digits in the tenths place. The decimal with the larger digit in the tenths place is greater.
Continue to the Right: If the tenths digits are also equal, continue comparing digits in the hundredths, thousandths, and subsequent places until you find digits that are different.
Trailing Zeros: Remember that adding trailing zeros to the right of the last digit after the decimal point does not change the value of the decimal. For example, 0.5 is the same as 0.50 and 0.500. This can be useful when comparing decimals with different numbers of decimal places.

1.3. Common Pitfalls to Avoid

Ignoring Place Value: Failing to consider place value can lead to incorrect comparisons. For instance, thinking that 0.09 is greater than 0.9 because 9 is greater than 0.
Stopping Too Early: Sometimes, the difference between two decimals is only apparent after comparing several decimal places. Always continue comparing until you find a difference.
Forgetting Trailing Zeros: Not using trailing zeros when necessary can make comparison difficult. For example, comparing 0.3 and 0.35 directly might lead to confusion. Adding a trailing zero to 0.3 (making it 0.30) clarifies that 0.35 is larger.

2. Step-by-Step Guide to Comparing Decimals

Following a structured approach can simplify the process of comparing decimals. Here’s a step-by-step guide to help you accurately compare any set of decimal numbers.

2.1. Step 1: Align the Decimal Points

The first step in comparing decimals is to align the decimal points vertically. This ensures that you are comparing digits in the same place value.

Example:
Compare 3.45 and 3.6.

  3.45
  3.6

2.2. Step 2: Compare the Whole Number Parts

Begin by comparing the whole number parts of the decimals. The decimal with the larger whole number is the greater number.

Example:
Compare 3.45 and 4.6.

  3.45
  4.6

Since 4 is greater than 3, 4.6 > 3.45.

2.3. Step 3: Compare the Tenths Place

If the whole number parts are equal, move to the tenths place (the first digit to the right of the decimal point) and compare the digits.

Example:
Compare 3.45 and 3.6.

  3.45
  3.6

The whole number parts are equal (both are 3), so compare the tenths place. Since 6 is greater than 4, 3.6 > 3.45.

2.4. Step 4: Compare the Hundredths Place (If Necessary)

If the whole number and tenths places are equal, compare the hundredths place (the second digit to the right of the decimal point).

Example:
Compare 3.45 and 3.48.

  3.45
  3.48

The whole number and tenths places are equal (both are 3.4), so compare the hundredths place. Since 8 is greater than 5, 3.48 > 3.45.

2.5. Step 5: Continue Comparing as Needed

If the hundredths places are equal, continue comparing digits in the thousandths place, ten-thousandths place, and so on, until you find a difference.

Example:
Compare 3.4567 and 3.4569.

  3.4567
  3.4569

The whole number, tenths, hundredths, and thousandths places are equal (both are 3.456), so compare the ten-thousandths place. Since 9 is greater than 7, 3.4569 > 3.4567.

2.6. Step 6: Use Trailing Zeros for Clarity

When decimals have different numbers of decimal places, adding trailing zeros can make the comparison easier.

Example:
Compare 3.4 and 3.45.

  3.4  (can be written as 3.40)
  3.45

Now, it is easier to compare: 3.45 > 3.40, so 3.45 > 3.4.

3. Comparing Decimals and Fractions

Decimals and fractions are two different ways of representing numbers that are not whole numbers. Converting fractions to decimals and vice versa allows for easy comparison.

3.1. Converting Fractions to Decimals

To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number).

Example:
Convert 3/4 to a decimal.

3 ÷ 4 = 0.75

So, 3/4 is equal to 0.75.

3.2. Converting Decimals to Fractions

To convert a decimal to a fraction, write the decimal as a fraction with a denominator of 10, 100, 1000, or another power of 10, depending on the number of decimal places. Then, simplify the fraction if possible.

Example:
Convert 0.45 to a fraction.

0.45 = 45/100

Simplify the fraction:

45/100 = 9/20

So, 0.45 is equal to 9/20.

3.3. Comparing Fractions and Decimals

Once you have both numbers in the same format (either both as decimals or both as fractions), you can compare them.

Example:
Compare 3/4 and 0.8.

First, convert 3/4 to a decimal:

3 ÷ 4 = 0.75

Now, compare 0.75 and 0.8.

0.  75
1.  80 (adding a trailing zero for clarity)

Since 0.80 > 0.75, 0.8 > 3/4.

A visual comparison using a number line helps to understand that 0.8 is greater than 0.75, which is equivalent to 3/4, reinforcing the understanding when comparing the value of decimals.

4. Using Number Lines for Decimal Comparison

A number line is a visual tool that can help you compare decimals by representing them as points on a line. This method is particularly useful for students who are visual learners.

4.1. Creating a Decimal Number Line

Draw a Line: Draw a straight line.
Mark the Integers: Mark whole numbers (integers) on the line at equal intervals. For example, mark 0, 1, 2, 3, and so on.
Divide into Tenths: Divide each interval between the integers into ten equal parts to represent tenths.
Label the Tenths: Label each tenth as 0.1, 0.2, 0.3, and so on.
Divide into Hundredths (Optional): For more precise comparisons, you can further divide each tenth into ten equal parts to represent hundredths.

4.2. Plotting Decimals on the Number Line

To plot a decimal on the number line, locate the point that corresponds to its value.

Example:
Plot 2.3 and 2.7 on a number line.

Locate the Integer: Find the whole number part of the decimal on the number line (in this case, 2).
Move to the Right: Move to the right along the number line to the tenth that corresponds to the decimal part. For 2.3, move to the third tenth mark after 2. For 2.7, move to the seventh tenth mark after 2.

4.3. Comparing Decimals Using the Number Line

Decimals that are further to the right on the number line are greater than decimals that are further to the left.

Example:
Compare 2.3 and 2.7 using the number line.

Since 2.7 is to the right of 2.3 on the number line, 2.7 > 2.3.

5. Real-World Applications of Decimal Comparison

Understanding how to compare decimals is useful in various real-world applications.

5.1. Financial Calculations

In finance, comparing decimals is essential for tasks such as:

Calculating Interest Rates: Comparing interest rates (e.g., 3.25% vs. 3.5%) to find the best investment or loan.
Determining Prices: Comparing prices of items in different stores to find the best deal (e.g., $2.49 vs. $2.50).
Budgeting: Tracking expenses and income, which often involve decimal amounts.

5.2. Measurements

In measurements, decimal comparison is crucial for:

Scientific Experiments: Comparing measurements from experiments to analyze data (e.g., 2.56 cm vs. 2.57 cm).
Construction and Engineering: Ensuring precision in measurements for building and design projects.
Cooking: Following recipes that require precise measurements of ingredients (e.g., 2.25 cups vs. 2.5 cups).

5.3. Data Analysis

In data analysis, comparing decimals is important for:

Statistics: Comparing statistical values to draw conclusions from data sets.
Analytics: Analyzing data in business and marketing to identify trends and make informed decisions.
Research: Comparing numerical data in scientific and academic research.

6. Advanced Techniques for Decimal Comparison

As you become more comfortable with comparing decimals, you can explore advanced techniques to handle more complex scenarios.

6.1. Scientific Notation

Scientific notation is used to express very large or very small numbers in a compact form. Comparing numbers in scientific notation involves comparing the exponents and the decimal parts.

Format: A number in scientific notation is written as ( a times 10^b ), where ( a ) is a decimal number between 1 and 10, and ( b ) is an integer exponent.
Comparison:
1. Compare Exponents: If the exponents are different, the number with the larger exponent is greater.
2. Compare Decimal Parts: If the exponents are the same, compare the decimal parts ( a ) as you would with regular decimals.

Example:
Compare ( 2.5 times 10^5 ) and ( 3.1 times 10^4 ).

Since the exponent 5 is greater than 4, ( 2.5 times 10^5 > 3.1 times 10^4 ).

Example:
Compare ( 4.2 times 10^3 ) and ( 3.8 times 10^3 ).

The exponents are the same, so compare the decimal parts. Since 4.2 > 3.8, ( 4.2 times 10^3 > 3.8 times 10^3 ).

6.2. Recurring Decimals

Recurring decimals (also known as repeating decimals) have a pattern of digits that repeats indefinitely. To compare recurring decimals, identify the repeating pattern and compare the decimals up to a sufficient number of places to determine which is greater.

Notation: Recurring decimals are often denoted with a bar over the repeating digits (e.g., ( 0.overline{3} ) means 0.333…).
Comparison:
1. Expand the Repeating Pattern: Write out the repeating pattern for several places.
2. Compare as Regular Decimals: Compare the expanded decimals as you would with regular decimals.

Example:
Compare ( 0.overline{3} ) and ( 0.33 ).

Expand ( 0.overline{3} ) to several places: ( 0.3333… )
Compare ( 0.3333 ) and ( 0.33 ).
Since ( 0.3333 > 0.33 ), ( 0.overline{3} > 0.33 ).

6.3. Approximations and Rounding

In some cases, it may be necessary to approximate or round decimals before comparing them, especially when dealing with irrational numbers or complex calculations.

Rounding: Round decimals to a specific number of decimal places to simplify the comparison.
Approximation: Use known approximations for irrational numbers like ( pi ) (approximately 3.14159) to compare them with other decimals.

Example:
Compare ( pi ) and 3.14.

Using the approximation ( pi approx 3.14159 ), we can compare ( 3.14159 ) and ( 3.14 ).
Since ( 3.14159 > 3.14 ), ( pi > 3.14 ).

7. Tips and Tricks for Mastering Decimal Comparison

To become proficient in comparing decimals, consider the following tips and tricks:

7.1. Practice Regularly

Consistent practice is key to mastering any skill. Work through various examples and exercises to reinforce your understanding of decimal comparison.

7.2. Use Visual Aids

Number lines and place value charts can be valuable tools for visualizing decimals and making comparisons easier.

7.3. Relate to Real-World Scenarios

Think about how decimal comparison is used in everyday situations, such as shopping, cooking, or managing finances. This can help you better understand the practical applications of the concept.

7.4. Understand Common Decimal Equivalents

Memorize common decimal equivalents for fractions, such as ( frac{1}{2} = 0.5 ), ( frac{1}{4} = 0.25 ), and ( frac{3}{4} = 0.75 ). This can speed up comparisons when dealing with fractions and decimals.

7.5. Check Your Work

Always double-check your comparisons to ensure accuracy. Mistakes can easily occur if you are not careful, especially when dealing with long or complex decimals.

8. FAQs About Comparing Decimals

Q1: What is the first step when comparing decimals?
A1: The first step is to align the decimal points vertically to ensure you are comparing digits in the same place value.

Q2: How do you compare decimals with different numbers of decimal places?
A2: Add trailing zeros to the decimal with fewer decimal places to make the comparison easier. For example, compare 0.5 and 0.55 by writing 0.5 as 0.50.

Q3: Can you compare a fraction and a decimal directly?
A3: No, you need to convert either the fraction to a decimal or the decimal to a fraction before comparing them.

Q4: What is a number line, and how can it help in comparing decimals?
A4: A number line is a visual tool that represents numbers as points on a line. Decimals that are further to the right on the number line are greater than decimals that are further to the left.

Q5: Why is understanding place value important when comparing decimals?
A5: Place value determines the value of each digit in a decimal number. Understanding place value is essential for accurately comparing digits in the tenths, hundredths, thousandths, and subsequent places.

Q6: How do you convert a fraction to a decimal?
A6: To convert a fraction to a decimal, divide the numerator (top number) by the denominator (bottom number).

Q7: What are trailing zeros, and why are they important in decimal comparison?
A7: Trailing zeros are zeros added to the right of the last digit after the decimal point. They do not change the value of the decimal but can make comparison easier by ensuring both decimals have the same number of decimal places.

Q8: How do you compare recurring decimals?
A8: Identify the repeating pattern and compare the decimals up to a sufficient number of places to determine which is greater.

Q9: What is scientific notation, and how is it used in decimal comparison?
A9: Scientific notation is used to express very large or very small numbers in a compact form. Comparing numbers in scientific notation involves comparing the exponents and the decimal parts.

Q10: Why is decimal comparison important in real-world scenarios?
A10: Decimal comparison is essential in various real-world applications, such as financial calculations, measurements, and data analysis.

9. COMPARE.EDU.VN: Your Partner in Decimal Mastery

At COMPARE.EDU.VN, we understand the importance of mastering decimal comparison. Whether you are a student, a professional, or simply someone looking to improve your math skills, we are here to help.

9.1. Comprehensive Guides

Our website offers comprehensive guides on various math topics, including decimal comparison. These guides provide step-by-step instructions, examples, and practice exercises to help you master the concepts.

9.2. Interactive Tools

We offer interactive tools and calculators that can help you compare decimals quickly and accurately. These tools can be particularly useful for checking your work and reinforcing your understanding.

9.3. Expert Support

Our team of math experts is available to provide support and answer any questions you may have about decimal comparison or other math topics.

9.4. Real-World Examples

We provide real-world examples and case studies that illustrate how decimal comparison is used in various industries and applications. This can help you better understand the practical relevance of the concept.

9.5. Continuous Learning

We continuously update our content and resources to ensure that you have access to the latest information and best practices in decimal comparison.

10. Conclusion: Mastering Decimal Comparison for Success

Comparing the value of decimals the correct sequence is a fundamental skill that is essential for success in various aspects of life. By understanding place value, following a step-by-step approach, and practicing regularly, you can master this skill and improve your accuracy in financial calculations, measurements, data analysis, and more.

Remember to align decimal points, compare whole numbers first, and then proceed to compare digits in the tenths, hundredths, and subsequent places. Use trailing zeros for clarity and convert fractions to decimals when necessary. Utilize number lines and place value charts to visualize decimals and make comparisons easier.

With the comprehensive guides, interactive tools, and expert support available at COMPARE.EDU.VN, you can confidently tackle any decimal comparison challenge. Visit our website today to start your journey toward decimal mastery and unlock new opportunities for success.

Are you ready to make smarter, more informed decisions? Visit compare.edu.vn today at 333 Comparison Plaza, Choice City, CA 90210, United States. For any inquiries, reach out via Whatsapp at +1 (626) 555-9090. Let us help you compare and choose with confidence.