Comparing is a fundamental concept in mathematics that allows us to understand the relationship between numbers and quantities. It involves determining whether one value is greater than, less than, or equal to another. This process is essential for making sense of data, solving problems, and understanding the world around us. This article will delve into the various aspects of comparing, from basic number comparisons to more complex comparisons involving fractions, decimals, and rational numbers.
Comparing Numbers: The Basics
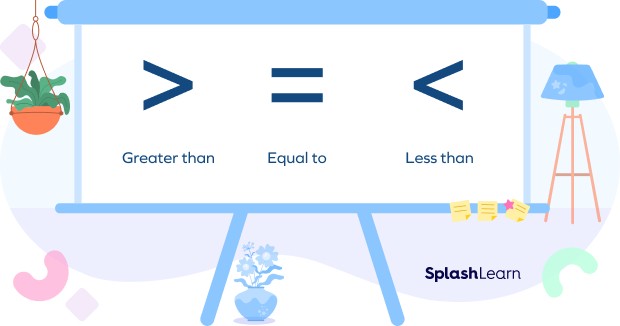
At its core, comparing involves examining two or more values and determining their relative magnitude. We use three primary symbols to represent these relationships:
- > (Greater than): Indicates that the value on the left is larger than the value on the right. For example, 7 > 3.
- < (Less than): Indicates that the value on the left is smaller than the value on the right. For example, 3 < 7.
- = (Equal to): Indicates that both values are the same. For example, 5 = 5.
Visual aids, like the image above, can help illustrate these concepts. Eight purple blocks are clearly more than six green blocks, demonstrating 8 > 6.
Comparing with Visual Representation
Using visual representations like blocks can make comparing numbers easier to understand.
The image above shows how comparing can be visualized:
- 8 > 6: Eight purple blocks are more than six green blocks.
- 5 = 5: Five orange blocks on each side represent equal quantities.
- 6 < 8: Six pink blocks are fewer than eight blue blocks.
Comparing and Finding the Difference
Comparing also allows us to determine the difference between two numbers, indicating how much larger or smaller one is compared to the other.
For example:
- Seven is greater than three by four (7 – 3 = 4).
- Three is less than six by three (6 – 3 = 3).
Comparing on a Number Line
A number line provides a visual representation of the order of numbers.
- Numbers to the right are greater than numbers to the left.
- Numbers to the left are less than numbers to the right.
For example, on a number line, -6 is to the left of 5, therefore -6 < 5.
Comparing Whole Numbers: A Step-by-Step Approach
Comparing whole numbers involves a systematic approach:
- Compare the number of digits: A number with more digits is larger.
- Compare the highest place value: If the number of digits is the same, compare the leftmost digits.
- Compare subsequent place values: If the highest place values are the same, compare the next digits to the right, and so on.
Comparing Integers: Positive and Negative Numbers
Comparing integers considers both positive and negative numbers:
- Positive integers are compared like whole numbers.
- Positive integers are always greater than negative integers.
- When comparing two negative integers, the number with the smaller absolute value is greater. For example, -3 > -7.
Comparing Fractions: Like and Unlike Fractions
Comparing fractions involves understanding their relative sizes:
- Like fractions (same denominator): Compare the numerators. The fraction with the larger numerator is greater. For Example: 7/8 > 5/8 because 7 > 5.
- Unlike fractions (different denominators): Use techniques like cross-multiplication or finding a common denominator to compare.
Comparing Decimals: A Place Value Approach
Comparing decimals involves a similar process to comparing whole numbers, focusing on place value:
- Compare the whole number parts.
- Compare the tenths place.
- Compare the hundredths place, and so on.
Comparing Rational Numbers: Extending Fraction Concepts
Comparing rational numbers builds upon the principles of comparing fractions, considering both positive and negative values.
Comparing in Real Life: Practical Applications
Comparing is crucial in everyday situations, such as:
- Comparing prices of items
- Comparing distances between locations. For instance, 4 miles (7040 yards) is greater than 7000 yards.
- Comparing weights of objects. As an example, 3 pounds (48 ounces) is greater than 40 ounces.
- Comparing volumes of liquids. For instance 2 liters (2000 ml) is less than 2700 ml.
Conclusion
Comparing is a foundational mathematical skill that enables us to analyze and interpret numerical information. From basic number comparisons to more complex comparisons involving fractions, decimals, and rational numbers, the ability to compare is crucial for problem-solving and understanding quantitative relationships in various contexts. Mastery of this skill empowers individuals to make informed decisions and navigate the world with greater confidence.