Comparing fractions involves determining which fraction is larger or smaller. Since fractions represent parts of a whole, comparing them requires understanding their relationship to one another. This guide explores various methods for comparing fractions effectively.
Understanding Fractions: A Foundation for Comparison
Before diving into comparison techniques, let’s review the basics of fractions. A fraction represents a part of a whole, expressed as a numerator (top number) over a denominator (bottom number), separated by a fraction bar. The numerator indicates how many parts are being considered, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator, and 4 is the denominator.
Comparing Fractions with Like Denominators
When two fractions share the same denominator, comparing them is straightforward. The fraction with the larger numerator represents the larger portion of the whole. For instance, when comparing 5/8 and 3/8, both fractions have a denominator of 8. Since 5 is greater than 3, 5/8 is larger than 3/8.
Comparing Fractions with Unlike Denominators: Finding Common Ground
Comparing fractions with different denominators requires a bit more work. The key is to find a common denominator, allowing for a direct comparison of the numerators. Here are two common methods:
1. Least Common Multiple (LCM)
The LCM of two numbers is the smallest number that both numbers divide into evenly. To compare fractions using the LCM:
- Find the LCM of the two denominators.
- Convert each fraction to an equivalent fraction with the LCM as the denominator.
- Compare the numerators of the new fractions. The fraction with the larger numerator is the larger fraction.
Example: Compare 2/3 and 3/4
- The LCM of 3 and 4 is 12.
- Convert 2/3 to 8/12 (multiply both numerator and denominator by 4).
- Convert 3/4 to 9/12 (multiply both numerator and denominator by 3).
- Since 9 > 8, 3/4 > 2/3.
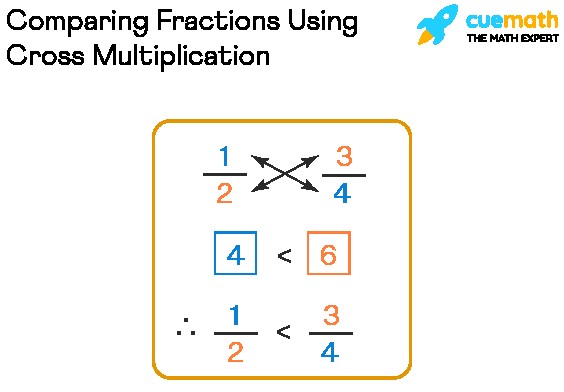
2. Cross-Multiplication: A Shortcut
Cross-multiplication offers a quicker way to compare fractions:
- Multiply the numerator of the first fraction by the denominator of the second fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the two products. The larger product corresponds to the larger fraction.
Example: Compare 2/3 and 3/4
- 2 x 4 = 8
- 3 x 3 = 9
- Since 9 > 8, 3/4 > 2/3.
Visualizing Fraction Comparison
Using visual aids like pie charts or number lines can help understand fraction comparisons. Representing fractions visually clarifies the relative sizes of the portions being compared.
Decimal Conversion: An Alternative Approach
Converting fractions to decimals provides another method for comparison:
- Divide the numerator by the denominator for each fraction.
- Compare the resulting decimals. The larger decimal represents the larger fraction.
Example: Compare 2/3 and 3/4
- 2/3 ≈ 0.67
- 3/4 = 0.75
- Since 0.75 > 0.67, 3/4 > 2/3
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics. By understanding the concepts of common denominators, cross-multiplication, visualization, and decimal conversion, you can confidently determine the relative sizes of fractions and solve problems involving fractional comparisons. Practice these methods to strengthen your understanding and build a solid foundation in fractions.