Comparing fractions involves determining which fraction is larger or smaller than another. Since fractions represent parts of a whole, comparing them requires understanding their relative size. This article explores various methods to compare fractions effectively.
Understanding Fractions
Before diving into comparison methods, let’s review what a fraction represents. A fraction consists of two parts:
- Numerator: The top number, indicating how many parts of the whole are being considered.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 3/5, 3 is the numerator and 5 is the denominator. This fraction represents three out of five equal parts of a whole.
Comparing Fractions with Like Denominators
When two fractions have the same denominator, comparing them is straightforward. The fraction with the larger numerator is the larger fraction.
Example: Compare 3/8 and 5/8.
Both fractions have a denominator of 8. Since 5 is greater than 3, 5/8 is larger than 3/8.
Comparing Fractions with Unlike Denominators
Comparing fractions with different denominators requires a few extra steps. The goal is to convert the fractions to equivalent fractions with a common denominator. One common method is using the Least Common Multiple (LCM).
Example: Compare 2/3 and 3/4.
- Find the LCM of the denominators: The LCM of 3 and 4 is 12.
- Create equivalent fractions:
- Multiply 2/3 by 4/4: (2 x 4) / (3 x 4) = 8/12
- Multiply 3/4 by 3/3: (3 x 3) / (4 x 3) = 9/12
- Compare the numerators: Since 9 is greater than 8, 9/12 (or 3/4) is larger than 8/12 (or 2/3).
Decimal Method for Comparing Fractions
Another approach is to convert each fraction into its decimal equivalent. Divide the numerator by the denominator to obtain the decimal value. Then, compare the decimals.
Example: Compare 5/8 and 7/12.
- 5/8 = 0.625
- 7/12 = 0.583
Since 0.625 is greater than 0.583, 5/8 is larger than 7/12.
Visualizing Fraction Comparison
Visual aids like pie charts or fraction bars can help illustrate the relative size of fractions. The fraction representing a larger portion of the whole is the larger fraction.
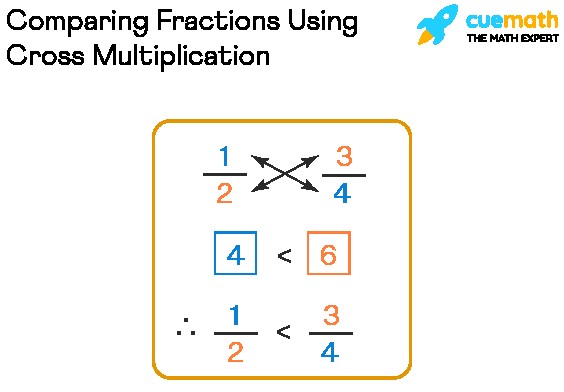
Cross-Multiplication Method
This method involves multiplying the numerator of one fraction by the denominator of the other, and vice versa.
Example: Compare 1/2 and 3/4.
- 1 x 4 = 4
- 3 x 2 = 6
Since 6 is greater than 4, 3/4 is larger than 1/2.
Conclusion
Comparing fractions is a fundamental math skill. By understanding the different methods outlined in this article—comparing like denominators, finding common denominators, converting to decimals, visualizing, and cross-multiplying—you can confidently determine the relative size of fractions. Choosing the most efficient method often depends on the specific fractions being compared.