What Does Compared Mean In Math? It’s a question that unlocks a fundamental understanding of mathematical relationships. This article, brought to you by COMPARE.EDU.VN, delves deep into the concept of comparison in mathematics, exploring its definition, application, and significance. We aim to provide clarity and practical insights, ensuring you grasp the essence of mathematical comparison.
1. Understanding the Core of Comparison in Math
1.1 Defining “Compared” in a Mathematical Context
In mathematics, “compared” refers to the process of examining two or more quantities, values, or mathematical objects to determine their similarities, differences, and relative magnitudes. It’s about establishing a relationship between these entities based on specific criteria, such as size, quantity, or order. This fundamental operation forms the basis for various mathematical concepts and problem-solving techniques. Comparison allows us to understand how different elements relate to each other and to make informed decisions based on these relationships.
1.2 The Importance of Comparison in Mathematical Reasoning
Comparison is not just a basic operation; it’s a cornerstone of mathematical reasoning. It allows us to:
- Establish order: Determine which quantity is greater, smaller, or equal.
- Identify patterns: Recognize relationships and trends between different sets of data.
- Solve problems: Formulate equations and inequalities to find unknown values.
- Make informed decisions: Analyze data and choose the best course of action based on numerical evidence.
Without comparison, mathematics would lack the ability to analyze, interpret, and draw meaningful conclusions from numerical information. It is vital for analytical thinking.
2. Methods and Techniques for Comparing Numbers
2.1 Using the Number Line as a Visual Aid
The number line is a powerful tool for visualizing and comparing numbers. Numbers are arranged in ascending order from left to right, making it easy to determine their relative positions.
- Numbers to the right are always greater than numbers to the left.
- The distance between two numbers represents the magnitude of their difference.
- The number line can be used to compare integers, rational numbers, and even real numbers.
 Number Line Example
Number Line Example
2.2 Comparing Whole Numbers: Digit Counting and Place Value
When comparing whole numbers, we can use two primary methods:
- Digit Counting: The number with more digits is generally greater. For example, 1,234 is greater than 987 because it has four digits while 987 only has three.
- Place Value: If the numbers have the same number of digits, we compare the digits from left to right, starting with the highest place value. The number with the larger digit in the highest place value is greater. For example, 567 is greater than 499 because 5 (in the hundreds place) is greater than 4.
2.3 Comparing Fractions: Finding Common Denominators
Comparing fractions requires a bit more effort. The most common method is to find a common denominator:
- Find the Least Common Multiple (LCM): Determine the LCM of the denominators of the fractions you want to compare.
- Convert Fractions: Convert each fraction to an equivalent fraction with the LCM as the denominator.
- Compare Numerators: Once the fractions have the same denominator, simply compare their numerators. The fraction with the larger numerator is the greater fraction.
For example, to compare 2/3 and 3/4:
- LCM of 3 and 4 is 12.
- 2/3 = 8/12
- 3/4 = 9/12
- Since 9 > 8, 3/4 is greater than 2/3.
2.4 Comparing Decimals: Aligning Decimal Points
Comparing decimals is similar to comparing whole numbers, but we need to align the decimal points first:
- Align Decimal Points: Write the decimals vertically, aligning the decimal points.
- Add Trailing Zeros: If necessary, add trailing zeros to the decimal with fewer digits after the decimal point so that both decimals have the same number of digits after the decimal point.
- Compare Digits: Compare the digits from left to right, starting with the whole number part. The decimal with the larger digit in the highest place value is greater.
For example, to compare 3.14 and 3.141:
-
Align decimal points:
3.14
3.141 -
Add trailing zero:
3.140
3.141 -
Compare digits: Since 1 is greater than 0 in the thousandths place, 3.141 is greater than 3.14.
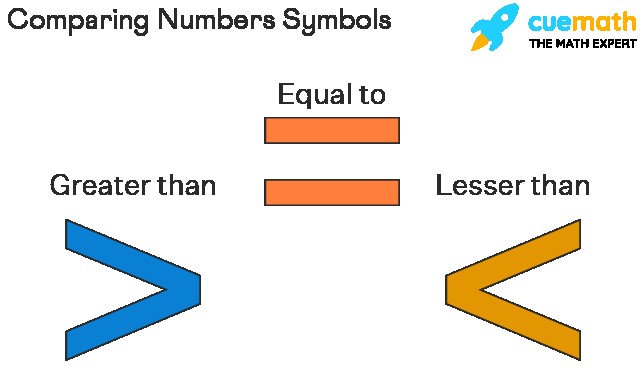
3. Essential Symbols Used in Mathematical Comparisons
3.1 The Greater Than Symbol (>) and Its Applications
The “greater than” symbol (>) indicates that one value is larger than another. For example:
- 5 > 3 (5 is greater than 3)
- x > 0 (x is greater than 0, meaning x is positive)
- a + b > c (the sum of a and b is greater than c)
3.2 The Less Than Symbol (<) and Its Role
The “less than” symbol (<) indicates that one value is smaller than another. For example:
- 2 < 7 (2 is less than 7)
- y < 10 (y is less than 10)
- p < q + r (p is less than the sum of q and r)
3.3 The Equal To Symbol (=) and Its Significance
The “equal to” symbol (=) indicates that two values are the same. For example:
- 4 = 4 (4 is equal to 4)
- a = b (a is equal to b)
- x + y = z (the sum of x and y is equal to z)
3.4 Combining Symbols: ≥ (Greater Than or Equal To) and ≤ (Less Than or Equal To)
These combined symbols provide a more inclusive comparison:
- ≥ (Greater Than or Equal To): Indicates that one value is either greater than or equal to another. For example, x ≥ 5 means x can be 5 or any number greater than 5.
- ≤ (Less Than or Equal To): Indicates that one value is either less than or equal to another. For example, y ≤ 10 means y can be 10 or any number less than 10.
4. Applying Comparison to Different Types of Numbers
4.1 Comparing Integers: Positive, Negative, and Zero
Comparing integers involves considering their signs and magnitudes:
- Positive integers are always greater than negative integers.
- Zero is greater than all negative integers and less than all positive integers.
- When comparing two positive integers, the one with the larger magnitude is greater.
- When comparing two negative integers, the one with the smaller magnitude is greater (e.g., -2 > -5).
4.2 Comparing Rational Numbers: Fractions and Decimals
We’ve already discussed the basics of comparing fractions and decimals. Here are some additional points:
- Converting between Fractions and Decimals: It can be helpful to convert fractions to decimals or vice versa to make comparisons easier.
- Using Benchmarks: Using benchmark fractions (like 1/2) or decimals (like 0.5) can provide a quick way to estimate and compare rational numbers.
4.3 Comparing Real Numbers: Including Irrational Numbers
Real numbers include all rational and irrational numbers. Comparing real numbers can be more challenging, especially when dealing with irrational numbers like √2 or π:
- Approximations: Use approximations to compare irrational numbers. For example, √2 ≈ 1.414 and π ≈ 3.142.
- Number Line: Visualize the numbers on a number line to get a sense of their relative positions.
5. Ordering Numbers: Ascending and Descending Order
5.1 Understanding Ascending Order: From Smallest to Largest
Ascending order is arranging numbers from the smallest to the largest. For example, the ascending order of the numbers 5, 2, 8, 1, 9 is 1, 2, 5, 8, 9.
5.2 Understanding Descending Order: From Largest to Smallest
Descending order is arranging numbers from the largest to the smallest. For example, the descending order of the numbers 5, 2, 8, 1, 9 is 9, 8, 5, 2, 1.
5.3 Practical Examples of Ordering Numbers in Real-World Scenarios
Ordering numbers has numerous practical applications:
- Sorting data: Arranging data in ascending or descending order makes it easier to analyze and interpret.
- Ranking: Ranking items based on their values, such as test scores or sales figures.
- Prioritization: Prioritizing tasks or items based on their importance or urgency.
6. Applying Comparison and Ordering in Algebraic Equations and Inequalities
6.1 Solving Inequalities Using Comparison Principles
Inequalities are mathematical statements that compare two expressions using symbols like >, <, ≥, or ≤. Solving inequalities involves finding the range of values that satisfy the inequality. The principles of comparison are crucial in this process.
6.2 Graphing Inequalities on a Number Line
Graphing inequalities on a number line provides a visual representation of the solution set. For example:
- x > 3 is represented by an open circle at 3 and a line extending to the right.
- x ≤ -2 is represented by a closed circle at -2 and a line extending to the left.
6.3 Using Comparison to Determine the Validity of Equations
Comparison can be used to check the validity of equations by substituting values and verifying that both sides of the equation are equal.
7. Common Mistakes to Avoid When Comparing Numbers
7.1 Ignoring Negative Signs
A frequent error is overlooking the impact of negative signs, leading to incorrect comparisons, particularly when dealing with integers and rational numbers. Always remember that negative numbers are less than zero, and the further a negative number is from zero, the smaller it is. For example, -5 is less than -2, even though 5 is greater than 2.
7.2 Forgetting to Find a Common Denominator When Comparing Fractions
When comparing fractions, it’s essential to find a common denominator before comparing the numerators. Failing to do so can result in incorrect comparisons. For example, when comparing 1/3 and 1/4, you can’t directly compare the numerators. You need to find a common denominator, such as 12, and convert the fractions to 4/12 and 3/12, respectively. Then you can accurately compare them.
7.3 Misinterpreting Decimal Place Values
Misunderstanding decimal place values can lead to errors in comparison. Make sure to align the decimal points and compare digits in the same place value columns. For instance, 0.25 is greater than 0.2 because 0.2 can be thought of as 0.20, and 25 is greater than 20.
7.4 Not Considering All Possible Solutions in Inequalities
When solving inequalities, remember to consider all possible solutions. An inequality often has a range of values that satisfy it, rather than a single solution. For example, the inequality x > 3 means that x can be any number greater than 3, not just 4.
8. Advanced Comparison Techniques
8.1 Comparing Numbers in Different Bases (Binary, Hexadecimal, etc.)
Comparing numbers in different bases requires converting them to a common base, usually base 10, before comparing. For example, to compare 1101 (binary) and 15 (decimal), convert 1101 to decimal (13) and then compare it to 15.
8.2 Using Logarithms to Compare Exponential Values
Logarithms can be used to compare exponential values by transforming them into linear values. For example, to compare 2^10 and 3^7, take the logarithm of both sides and compare the resulting values.
8.3 Comparing Sets Using Set Theory Principles
Comparing sets involves using set theory principles such as cardinality (the number of elements in a set) and set operations (union, intersection, difference) to determine relationships between sets.
9. Real-World Applications of Mathematical Comparison
9.1 Financial Analysis: Comparing Investments and Interest Rates
In financial analysis, comparison is used to evaluate investment options, compare interest rates, and assess financial performance.
9.2 Data Analysis: Identifying Trends and Outliers
In data analysis, comparison is used to identify trends, outliers, and patterns in data sets.
9.3 Scientific Research: Comparing Experimental Results and Control Groups
In scientific research, comparison is used to compare experimental results with control groups and to draw conclusions about the effectiveness of treatments or interventions.
9.4 Everyday Decision-Making: Budgeting, Shopping, and Time Management
In everyday life, we use comparison to make decisions about budgeting, shopping, time management, and other practical matters.
10. How COMPARE.EDU.VN Can Help You Master Mathematical Comparisons
10.1 Access to Comprehensive Comparison Guides and Tutorials
COMPARE.EDU.VN offers a wealth of resources to help you master mathematical comparisons. Our comprehensive guides and tutorials provide step-by-step instructions, examples, and practice problems to reinforce your understanding.
10.2 Interactive Tools and Resources for Practice
Our interactive tools and resources provide a hands-on learning experience. Use our comparison calculators, number line visualizers, and other tools to practice comparing numbers and solving inequalities.
10.3 Expert Insights and Tips for Efficient Problem-Solving
Benefit from the expertise of our team of mathematics educators. We provide valuable insights, tips, and strategies to help you solve problems efficiently and accurately.
10.4 Personalized Learning Paths Tailored to Your Needs
COMPARE.EDU.VN offers personalized learning paths tailored to your specific needs and goals. Whether you’re a student, a professional, or simply someone who wants to improve their mathematical skills, we can help you achieve your objectives.
11. Frequently Asked Questions (FAQs) About Mathematical Comparison
1. What does “compare” mean in math?
In mathematics, “compare” means to examine two or more numbers, quantities, or mathematical objects to determine their similarities, differences, and relative magnitudes.
2. What are the basic symbols used for comparing numbers?
The basic symbols are: > (greater than), < (less than), = (equal to), ≥ (greater than or equal to), and ≤ (less than or equal to).
3. How do you compare fractions?
Find a common denominator, convert the fractions to equivalent fractions with the common denominator, and then compare the numerators.
4. How do you compare decimals?
Align the decimal points, add trailing zeros if necessary, and compare the digits from left to right.
5. What is ascending order?
Ascending order is arranging numbers from the smallest to the largest.
6. What is descending order?
Descending order is arranging numbers from the largest to the smallest.
7. How do you compare negative numbers?
Negative numbers are always less than zero. When comparing two negative numbers, the one with the smaller magnitude is greater (e.g., -2 > -5).
8. How do you solve inequalities?
Use the same principles as solving equations, but remember to reverse the inequality sign when multiplying or dividing by a negative number.
9. How can number lines help in comparing numbers?
Number lines provide a visual representation of the relative positions of numbers, making it easy to determine which numbers are greater or smaller.
10. What are some real-world applications of mathematical comparison?
Financial analysis, data analysis, scientific research, and everyday decision-making.
Mathematical comparison is a fundamental skill that underpins many areas of mathematics and everyday life. By understanding the concepts, techniques, and symbols involved, you can enhance your problem-solving abilities and make more informed decisions. Visit COMPARE.EDU.VN at 333 Comparison Plaza, Choice City, CA 90210, United States, or contact us via WhatsApp at +1 (626) 555-9090 to explore our comprehensive resources and take your mathematical skills to the next level. Let compare.edu.vn be your guide to mastering the art of comparison.