What Does Compare Mean in Math: Definitions and Applications

What Does Compare Mean In Math? This article from COMPARE.EDU.VN provides a comprehensive guide, exploring the meaning of comparison in mathematical contexts. This includes symbols, applications, and real-world examples, empowering you to confidently navigate numerical relationships and make informed decisions. Learn about mathematical comparisons, contrasting quantities, and understanding magnitudes for success in math and beyond.

1. Understanding “Compare” in Mathematics

In mathematics, “compare” signifies evaluating the relationship between two or more quantities to determine if they are equal or if one is greater or less than the other. This fundamental concept underpins various mathematical operations and problem-solving strategies. It’s not just about identifying differences; it’s about understanding the magnitude of those differences and the implications they hold.

Consider this: you’re deciding which smartphone to buy. You might compare their storage capacities (128GB vs. 256GB), camera resolutions (12MP vs. 48MP), or battery life (3000mAh vs. 4000mAh). Each comparison helps you assess which phone better meets your needs. Similarly, in finance, comparing interest rates on different loans (5% vs. 7%) helps you determine which option is more affordable.

This process of comparison extends far beyond simple numerical values. It applies to sets, functions, geometric shapes, and even abstract concepts. The core idea remains the same: to understand the relative properties and characteristics of different mathematical entities.

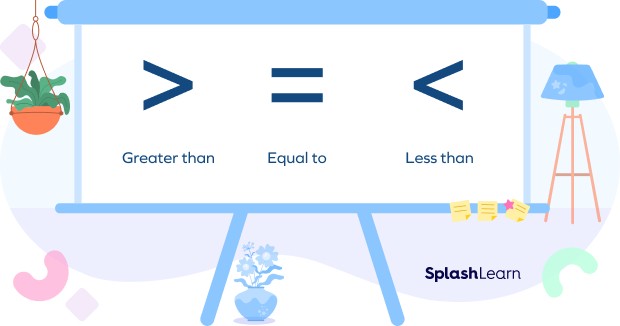
2. Essential Symbols for Mathematical Comparisons

Mastering the symbols used for comparisons is crucial for understanding and expressing mathematical relationships effectively. Here’s a breakdown of the key symbols:

Greater Than (>): Indicates that one value is larger than another. For example, 8 > 6 means “8 is greater than 6.”
Less Than (<): Indicates that one value is smaller than another. For example, 5 < 9 means “5 is less than 9.”
Equal To (=): Indicates that two values are the same. For example, 5 = 5 means “5 is equal to 5.”
Greater Than or Equal To (≥): Indicates that one value is larger than or equal to another. For example, x ≥ 7 means “x is greater than or equal to 7.”
Less Than or Equal To (≤): Indicates that one value is smaller than or equal to another. For example, y ≤ 3 means “y is less than or equal to 3.”
Not Equal To (≠): Indicates that two values are not the same. For example, a ≠ b means “a is not equal to b.”

These symbols are the language of comparison in mathematics, allowing us to express complex relationships concisely and unambiguously. The ability to interpret and use them correctly is fundamental to mathematical literacy.

3. Comparing Numbers on a Number Line

The number line provides a visual representation of numbers and their order, making comparisons intuitive. Key principles:

Right is Greater: On a horizontal number line, numbers to the right are always greater than numbers to the left.
Left is Smaller: Conversely, numbers to the left are always smaller than numbers to the right.

Example: Comparing -3 and 2 on the number line.

Imagine a number line stretching from negative infinity to positive infinity. Locate -3 and 2 on this line. You’ll notice that 2 lies to the right of -3. Therefore, 2 > -3, meaning 2 is greater than -3.

This simple visualization is particularly helpful when dealing with negative numbers, fractions, and decimals. It provides a concrete way to understand the relative positions and magnitudes of different numerical values.

4. Comparing Whole Numbers: A Step-by-Step Approach

Comparing whole numbers involves a systematic process to determine which number is larger. Here’s a step-by-step approach:

Step 1: Count the Digits: The number with more digits is generally the larger number. For instance, 1234 is greater than 987.
Step 2: Compare the Leading Digits: If the numbers have the same number of digits, compare the digits in the highest place value (the leftmost digit). The number with the larger leading digit is greater. For example, 5432 is greater than 4987 because 5 is greater than 4.
Step 3: Proceed to the Next Digit: If the leading digits are the same, move to the next digit to the right and compare those. Continue this process until you find a difference in the digits. For example, 7891 is greater than 7856 because 9 is greater than 5.
Step 4: All Digits are Equal: If all the digits are the same, the numbers are equal. For example, 1234 = 1234.

Example: Comparing 8,765 and 8,792.

Both numbers have four digits, and the leading digits are the same (8). The next digit is also the same (7). However, in the tens place, 9 is greater than 6. Therefore, 8,792 > 8,765.

This systematic approach ensures accurate comparisons, even with large whole numbers. This also increases numerical literacy and arithmetic competence.

5. Comparing Integers: Positive vs. Negative

When comparing integers (positive and negative whole numbers), the following principles apply:

Positive > Negative: Any positive integer is always greater than any negative integer. For example, 5 > -3.
Positive > Zero: Any positive integer is greater than zero. For example, 2 > 0.
Negative < Zero: Any negative integer is less than zero. For example, -1 < 0.
Comparing Negatives: When comparing two negative integers, the number with the smaller absolute value is greater. For example, -2 > -5 because -2 is closer to zero than -5.

Example: Comparing -7 and -4.

Both numbers are negative. The absolute value of -7 is 7, and the absolute value of -4 is 4. Since 4 is smaller than 7, -4 is greater than -7. Therefore, -4 > -7.

Understanding the relationship between positive and negative numbers is crucial for various mathematical concepts, including algebra, graphing, and calculus.

6. Comparing Fractions: Like vs. Unlike

Comparing fractions requires different approaches depending on whether the fractions have the same denominator (like fractions) or different denominators (unlike fractions).

6.1. Comparing Like Fractions

When fractions have the same denominator, simply compare the numerators. The fraction with the larger numerator is the greater fraction.

Example: Comparing 3/7 and 5/7.

Both fractions have the same denominator (7). Since 5 is greater than 3, 5/7 > 3/7.

6.2. Comparing Unlike Fractions

When fractions have different denominators, you need to find a common denominator before comparing the numerators. Two common methods are:

Finding a Common Denominator: Determine the least common multiple (LCM) of the denominators. Convert each fraction to an equivalent fraction with the LCM as the denominator. Then, compare the numerators as with like fractions.
Cross Multiplication: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Compare the resulting products. The fraction corresponding to the larger product is the greater fraction.

Example (Common Denominator): Comparing 2/5 and 3/8.

The LCM of 5 and 8 is 40. Convert the fractions:

2/5 = (2 8) / (5 8) = 16/40
3/8 = (3 5) / (8 5) = 15/40

Since 16 is greater than 15, 16/40 > 15/40. Therefore, 2/5 > 3/8.

Example (Cross Multiplication): Comparing 2/5 and 3/8.

2 * 8 = 16
3 * 5 = 15

Since 16 is greater than 15, 2/5 > 3/8.

Choosing the appropriate method depends on the specific fractions being compared. Finding a common denominator is generally more suitable when comparing multiple fractions, while cross multiplication is often quicker for comparing just two fractions.

7. Comparing Decimals: Aligning Place Values

Comparing decimals involves aligning the decimal points and comparing digits in each place value.

Step 1: Align Decimal Points: Write the decimals vertically, aligning the decimal points.
Step 2: Add Trailing Zeros: If necessary, add trailing zeros to the right of the decimal so that both numbers have the same number of decimal places.
Step 3: Compare Whole Number Parts: Compare the digits to the left of the decimal point. The number with the larger whole number part is greater.
Step 4: Compare Decimal Places: If the whole number parts are the same, compare the digits in the tenths place, then the hundredths place, and so on, until you find a difference.

Example: Comparing 12.345 and 12.35.

Align the decimal points:

12.345
12.350  (added trailing zero)

The whole number parts are the same (12), and the tenths place is the same (3). However, in the hundredths place, 5 is greater than 4. Therefore, 12.35 > 12.345.

This method ensures accurate comparisons, even when decimals have different numbers of decimal places.

8. Comparing Rational Numbers: A Unified Approach

Rational numbers encompass fractions, decimals, and integers. To compare rational numbers, convert them to a common form (either all fractions or all decimals) and then apply the appropriate comparison method. Remember these rules:

Positive > Negative: Any positive rational number is greater than any negative rational number.
Converting Fractions to Decimals: Divide the numerator by the denominator to convert a fraction to a decimal.
Converting Decimals to Fractions: Express the decimal as a fraction with a power of 10 as the denominator.

Example: Comparing -3/4 and -0.8.

Convert -3/4 to a decimal: -3/4 = -0.75.

Now compare -0.75 and -0.8. Since -0.75 is closer to zero than -0.8, -0.75 > -0.8. Therefore, -3/4 > -0.8.

By converting all rational numbers to a common form, you can easily apply the rules for comparing fractions or decimals.

9. Real-Life Applications of Comparing Numbers

Comparing numbers is an essential skill with numerous applications in everyday life:

Budgeting: Comparing prices of different products or services to make informed purchasing decisions. For example, comparing the cost per unit of two different brands of cereal to determine which is the better value.
Cooking: Adjusting ingredient quantities in recipes based on the desired serving size. For example, doubling a recipe requires multiplying all ingredient amounts by 2.
Travel: Comparing distances, travel times, and costs of different routes to plan efficient trips. For example, comparing the driving distance between two cities using different highway routes.
Investing: Comparing rates of return on different investment options to maximize profits. For example, comparing the interest rates offered by different banks on savings accounts.
Health: Monitoring vital signs like blood pressure and temperature to track health progress. For example, comparing daily blood pressure readings to identify trends and potential health concerns.
Time Management: Estimating and comparing time needed for various tasks to plan your schedule. For example, comparing the time required to complete different assignments to prioritize your workload.

These are just a few examples of how comparing numbers helps us make informed decisions and navigate the world around us.

10. Common Mistakes to Avoid When Comparing Numbers

While comparing numbers seems straightforward, certain common mistakes can lead to incorrect conclusions:

Ignoring Negative Signs: Forgetting that negative numbers are less than positive numbers and zero.
Misunderstanding Decimal Place Values: Incorrectly comparing digits in different decimal places (e.g., comparing the tenths place of one number to the hundredths place of another).
Not Finding a Common Denominator: Attempting to compare unlike fractions without first finding a common denominator.
Incorrectly Applying Cross Multiplication: Making errors during the cross-multiplication process, leading to incorrect product comparisons.
Not Aligning Decimal Points: Failing to align decimal points when comparing decimals, resulting in incorrect place value comparisons.
Overlooking Units: Not paying attention to the units of measurement when comparing quantities (e.g., comparing miles and kilometers without converting).

By being aware of these common pitfalls, you can improve your accuracy and avoid errors when comparing numbers.

11. Comparing Numbers in Algebra and Beyond

The concept of comparing numbers extends beyond basic arithmetic and plays a crucial role in more advanced mathematical topics:

Algebra: Solving inequalities involves comparing expressions and determining the range of values that satisfy the inequality. For example, solving the inequality x + 3 > 5 requires comparing the expression x + 3 to the value 5.
Calculus: Determining the limits of functions involves comparing the function’s value as the input approaches a certain value. For example, finding the limit of f(x) as x approaches infinity involves comparing the function’s value to increasingly large numbers.
Statistics: Comparing data sets to identify trends, patterns, and significant differences. For example, comparing the average test scores of two different classes to determine if there is a statistically significant difference.
Linear Programming: Optimizing solutions to problems by comparing different combinations of variables subject to certain constraints. For example, maximizing profit by comparing different production plans within resource limitations.

Understanding the concept of comparing numbers is essential for success in various branches of mathematics and its applications.

12. Tools and Resources for Mastering Number Comparisons

Many tools and resources are available to help you improve your number comparison skills:

Online Math Games: Interactive games that make learning fun and engaging. Websites like Khan Academy and Math Playground offer a variety of games focused on number comparison.
Worksheets: Practice problems that reinforce your understanding of different comparison techniques. Many websites offer free printable worksheets on number comparison.
Educational Videos: Visual explanations that break down complex concepts into easily digestible segments. YouTube channels like Numberphile and 3Blue1Brown offer excellent videos on mathematical concepts.
Tutoring: Personalized instruction from a qualified math tutor who can provide targeted support and guidance.
COMPARE.EDU.VN: Comprehensive articles and resources that explain mathematical concepts in a clear and concise manner.

By utilizing these resources, you can strengthen your understanding of number comparison and build your mathematical confidence.

13. Why is Comparing Numbers Important in Mathematics?

Comparing numbers is one of the fundamental skills of arithmetic and mathematics. This skill helps you in many ways:

Problem Solving: You are able to solve problems because you know the relative value of numbers.
Logical Thinking: The process of comparing numbers improves logical thinking and reasoning.
Decision-Making: Daily life is full of choices and comparing numbers helps in making choices.

14. Frequently Asked Questions (FAQs) About Comparing Numbers

Here are some frequently asked questions about comparing numbers:

What is the importance of comparing numbers in daily life?

Comparing numbers is vital for tasks like budgeting, cooking, travel planning, and making informed purchasing decisions.
How is comparing numbers different from ordering numbers?

Comparing numbers determines if values are equal or if one is greater or less than another, while ordering arranges numbers in ascending or descending order.
What’s a quick way to compare numbers?

Visualizing numbers on a number line can quickly determine their relative magnitudes.
How do you compare two fractions with different denominators?

Find a common denominator or use cross-multiplication to compare the fractions.
What is the first step in comparing two decimal numbers?

Align the decimal points and compare the whole number parts first.
How do you compare a positive and a negative number?

Positive numbers are always greater than negative numbers.
What should you do if you’re having trouble understanding number comparisons?

Utilize online games, worksheets, educational videos, or seek tutoring for personalized support.
How do the comparison of numbers play a role in algebra?

Algebra involves solving inequalities, which depends on comparing expressions and ranges.
How can comparison of numbers assist in statistical analysis?

Comparison of data sets and trends can point to patterns and variations.
Are there common mistakes to avoid when comparing?

Avoid not taking into account any negative signs, comparing decimals out of order, and not using any common denominators.

Conclusion: Mastering the Art of Mathematical Comparison

Understanding “what does compare mean in math” is a cornerstone of mathematical proficiency. It enables you to analyze relationships between numerical values, make informed decisions, and solve complex problems across various domains. Remember, mathematical comparison is about more than just finding differences; it’s about understanding the magnitude and implications of those differences.

By mastering the concepts, symbols, and techniques discussed in this article, you’ll be well-equipped to navigate the world of numbers with confidence.

Are you looking for a comprehensive resource to compare products, services, or ideas and make informed choices? Visit COMPARE.EDU.VN today.

Address: 333 Comparison Plaza, Choice City, CA 90210, United States

Whatsapp: +1 (626) 555-9090

Website: compare.edu.vn