Comparing numbers in mathematics involves determining the relative size or value of two or more numbers. This process establishes whether a number is greater than, less than, or equal to another number. Understanding comparison is fundamental to various mathematical concepts, from basic arithmetic to advanced calculus.
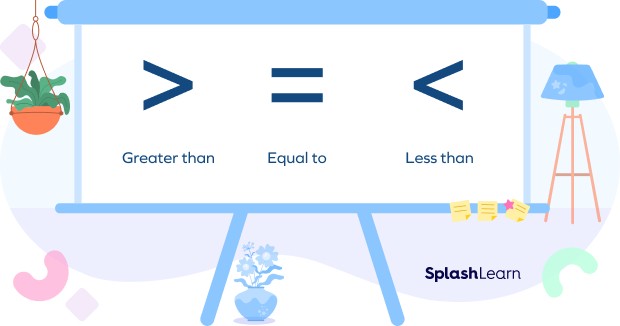
The symbols used for comparison are:
- >: Greater than
- <: Less than
- =: Equal to
For example, 8 > 6 (8 is greater than 6), 5 = 5 (5 is equal to 5), and 6 < 8 (6 is less than 8).
Comparing Numbers Using Visual Aids
Visual aids like number lines and blocks can help illustrate the concept of comparison.
In the image above, the blocks clearly demonstrate the relationships between the numbers. Comparing numbers also allows us to determine the difference between them.
Here, we see that 7 is greater than 3 by 4 (7 – 3 = 4), and 3 is less than 6 by 3 (6 – 3 = 3).
Comparing Numbers on a Number Line
A number line provides a clear visual representation of number comparison. Numbers to the right are greater than numbers to the left.
- A number on the right is always greater than a number on the left.
- A number on the left is always less than a number on the right.
For example, on a number line, -6 is to the left of 5, therefore -6 < 5.
Comparing Different Types of Numbers
The process for comparing numbers varies slightly depending on the type of numbers being compared.
Whole Numbers
Comparing whole numbers involves examining the number of digits and the value of each digit, starting from the leftmost position.
Integers
Comparing integers considers both positive and negative numbers. Remember:
- Positive integers are always greater than negative integers.
- When comparing two negative integers, the number with the smaller absolute value is greater.
Fractions
Comparing fractions can be done using cross-multiplication or by finding a common denominator:
- Cross-Multiplication: Multiply the numerator of the first fraction by the denominator of the second and vice versa. Compare the resulting products.
- Common Denominator: Convert the fractions to have the same denominator, then compare the numerators.
Decimals
Comparing decimals involves comparing the digits in each place value, starting from the leftmost position (before the decimal point) and moving to the right.
Rational Numbers
Comparing rational numbers (which include fractions and integers) often involves converting them to a common form, such as fractions with a common denominator, before comparison.
Real-World Applications of Comparing Numbers
Comparing numbers is crucial in everyday situations, such as:
- Comparing prices of items
- Measuring distances
- Assessing weights and volumes
- Analyzing data and statistics
Conclusion
Comparing numbers is a foundational skill in mathematics, enabling us to understand relationships between quantities and make informed decisions in various contexts. Mastering this skill is essential for success in higher-level math concepts and real-world problem-solving.