Comparing slopes in regression analysis is crucial for understanding how relationships between variables differ across groups or conditions. This post explains How To Statistically Compare Two Slopes using hypothesis testing and provides clear examples.
Understanding the Need for Slope Comparison
Linear regression helps establish relationships between variables. However, these relationships can change under different conditions or contexts. For instance, the relationship between advertising spend and sales might vary between different marketing campaigns. To determine if these changes are statistically significant, rather than just random variations, you need to compare the slopes of the regression lines. This process involves testing whether the slope coefficients are significantly different from each other.
Comparing Slopes: A Step-by-Step Approach
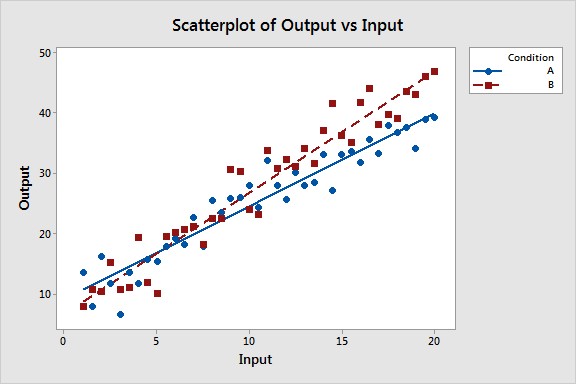
To compare slopes, you need to incorporate a categorical variable that represents the different conditions or groups you’re comparing. This variable allows you to model how the relationship between your independent and dependent variables changes based on the group membership. We’ll use an example where we compare the relationship between an “Input” variable and an “Output” variable under two different “Conditions” (A and B).
1. Introducing a Categorical Variable and Interaction Term:
- Create a categorical variable representing the groups or conditions. (e.g., Condition A and Condition B)
- Introduce an interaction term by multiplying the independent variable (Input) with the categorical variable (Condition). This interaction term allows the slope to vary based on the condition.
2. Performing Regression Analysis with the Interaction Term:
- Use statistical software (e.g., Minitab) to perform regression analysis. Include the independent variable (Input), the categorical variable (Condition), and the interaction term (Input*Condition) in your model. The output will include a coefficients table.
- Navigate to Stat > Regression > Regression > Fit Regression Model in Minitab. Include Output as the response variable, Input as the continuous predictor, and Condition as the categorical predictor. Then click on Model and add the interaction term.
3. Interpreting the Coefficients Table:
- Focus on the p-value associated with the interaction term (Input*Condition). A low p-value (typically less than 0.05) indicates a statistically significant difference between the slopes. Rejecting the null hypothesis suggests the slopes are significantly different.
4. Examining the Regression Equation:
- The regression equation will provide separate equations for each condition, revealing the different slopes and intercepts. This allows for a clear comparison of the relationships.
Conclusion
Statistically comparing two slopes allows you to confidently determine if observed differences in relationships are significant. By using a categorical variable and an interaction term in your regression model, you can test for these differences and draw meaningful conclusions about how relationships between variables change across different groups or conditions. Software packages like Minitab simplify this process, enabling you to focus on interpreting the results and understanding the practical implications of your findings.