Understanding fractions is a fundamental math skill. This guide focuses on How To Compare Unit Fractions, providing a clear, step-by-step approach with visual aids.
What is a Unit Fraction?
A unit fraction represents one equal part of a whole. It always has 1 as its numerator (the top number). The denominator (the bottom number) indicates how many equal parts the whole is divided into. For example, 1/4 (one-quarter) means one out of four equal parts.
The Golden Rule: Bigger Denominator, Smaller Fraction
The key to comparing unit fractions is understanding a simple rule: the larger the denominator, the smaller the unit fraction. This is because a larger denominator means the whole is divided into more pieces, making each piece smaller.
For example:
-
1/2 is greater than 1/3: A half is larger than a third because the whole is divided into fewer pieces.
-
1/5 is less than 1/4: A fifth is smaller than a quarter because the whole is divided into more pieces.
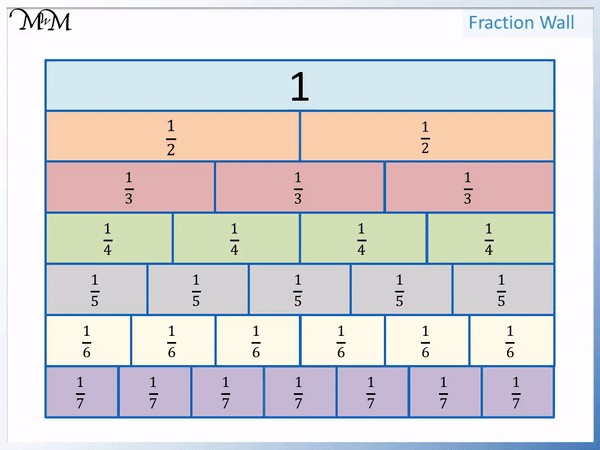
Visualizing with a Fraction Wall
A fraction wall is a great visual tool for comparing unit fractions. It represents a whole divided into different unit fractions. You can clearly see that 1/2 is larger than 1/3, which is larger than 1/4, and so on.
Using Inequality Symbols
We use symbols to show the relationship between fractions:
-
Greater than (>): The symbol points towards the smaller fraction. Example: 1/2 > 1/3
-
Less than (<): The symbol points towards the smaller fraction. Example: 1/7 < 1/4
Comparing Unit Fractions: Examples
Let’s compare some unit fractions:
1/3 vs. 1/4:
Since 4 is greater than 3, 1/4 is smaller than 1/3. We write this as 1/3 > 1/4.
1/7 vs. 1/4:
Since 7 is greater than 4, 1/7 is smaller than 1/4. We write this as 1/7 < 1/4.
Ordering Unit Fractions
To order unit fractions from smallest to largest, simply arrange them from the largest denominator to the smallest denominator.
Example: Order 1/5, 1/2, 1/6, and 1/3 from smallest to largest.
The denominators are 5, 2, 6, and 3. Arranging them from largest to smallest gives us 6, 5, 3, 2. Therefore, the order of the fractions from smallest to largest is 1/6, 1/5, 1/3, and 1/2.
By understanding the relationship between the denominator and the size of a unit fraction, you can easily compare and order them. Remember, practice makes perfect!