Comparing two values statistically is a crucial process in various fields, providing insights into differences and similarities. At COMPARE.EDU.VN, we offer straightforward methods and comprehensive resources to help you confidently navigate statistical comparisons and make informed decisions. Unlock the power of statistical analysis and comparative assessments to enhance your understanding of data variations and trends, ultimately leading to more effective solutions for data analysis and decision-making.
1. Understanding the Basics of Statistical Comparison
Before diving into the methods, it’s important to understand what statistical comparison entails and why it’s necessary. This section provides a foundation for those new to the concept, while also offering a refresher for those already familiar.
1.1 What is Statistical Comparison?
Statistical comparison involves using statistical methods to assess whether there is a significant difference between two or more sets of data. These sets can represent different groups, conditions, or treatments. The goal is to determine if observed differences are likely due to real effects or simply due to chance. This is critical in fields like medicine, engineering, and social sciences, where accurate comparisons can lead to important discoveries and decisions.
Statistical comparison is a cornerstone of evidence-based decision-making, allowing us to move beyond subjective evaluations to quantifiable and reliable assessments. This reduces biases and promotes more accurate conclusions.
1.2 Why Compare Values Statistically?
Statistical comparisons are essential for several reasons:
- Informed Decision-Making: They provide the data needed to make informed decisions based on solid evidence.
- Hypothesis Testing: Statistical tests help confirm or reject hypotheses, contributing to the advancement of knowledge.
- Quality Control: They ensure that products and processes meet certain standards by comparing them against benchmarks.
- Research Validation: They validate research findings by determining the significance of observed differences.
Without statistical comparison, we risk making decisions based on flawed assumptions or incomplete information. This could lead to inefficiencies, errors, or even harmful outcomes.
1.3 Key Concepts in Statistical Comparison
To effectively compare values statistically, you need to understand several key concepts:
- Hypothesis: A statement about the population that we want to test. It usually takes the form of a null hypothesis (no effect) and an alternative hypothesis (there is an effect).
- P-value: The probability of observing results as extreme as, or more extreme than, the data, assuming the null hypothesis is true.
- Significance Level (Alpha): A threshold used to determine whether the p-value is small enough to reject the null hypothesis. Common values are 0.05 or 0.01.
- Statistical Power: The probability of correctly rejecting the null hypothesis when it is false.
- Effect Size: A measure of the magnitude of the difference between groups. It provides more information than just whether the difference is statistically significant.
- Confidence Interval: A range of values that is likely to contain the true population parameter.
Understanding these concepts is crucial for interpreting the results of statistical tests and drawing meaningful conclusions. A solid grasp of these principles can prevent misinterpretations and ensure the validity of your analyses.
2. Choosing the Right Statistical Test
Selecting the appropriate statistical test is crucial for obtaining reliable and valid results. Different tests are designed for different types of data and research questions. This section provides a guide to help you choose the correct test for your specific needs.
2.1 Factors to Consider When Choosing a Test
Several factors should influence your choice of statistical test:
- Type of Data: Is your data continuous (e.g., height, weight) or categorical (e.g., gender, color)?
- Number of Groups: Are you comparing two groups or more than two?
- Independence: Are the data points independent of each other, or are they related (e.g., repeated measurements on the same subject)?
- Distribution: Does your data follow a normal distribution?
Answering these questions will help narrow down the list of suitable tests and ensure that the chosen test is appropriate for your data.
2.2 Common Statistical Tests for Comparing Two Values
Here are some of the most common statistical tests for comparing two values:
- T-test: Used to compare the means of two groups. There are different types of t-tests:
- Independent Samples T-test: For comparing the means of two independent groups.
- Paired Samples T-test: For comparing the means of two related groups (e.g., before and after measurements on the same subjects).
- Mann-Whitney U Test: A non-parametric test used to compare the medians of two independent groups when the data is not normally distributed.
- Wilcoxon Signed-Rank Test: A non-parametric test used to compare the medians of two related groups when the data is not normally distributed.
- Chi-Square Test: Used to compare categorical data, such as proportions or frequencies.
Each test has its own assumptions and requirements, so it’s important to understand these before applying the test to your data.
2.3 Examples of Test Selection Based on Scenario
To illustrate how to choose the right test, consider the following examples:
- Scenario 1: Comparing the average test scores of two different classes of students.
- Appropriate Test: Independent Samples T-test (assuming the data is normally distributed).
- Scenario 2: Comparing the blood pressure of patients before and after taking a new medication.
- Appropriate Test: Paired Samples T-test (assuming the data is normally distributed).
- Scenario 3: Comparing the income levels of two groups of people when the data is not normally distributed.
- Appropriate Test: Mann-Whitney U Test.
- Scenario 4: Comparing the proportion of males and females who prefer a certain product.
- Appropriate Test: Chi-Square Test.
These examples highlight the importance of considering the nature of your data and the specific research question when selecting a statistical test.
3. Step-by-Step Guide to Performing Statistical Comparisons
Once you’ve chosen the appropriate statistical test, the next step is to perform the comparison. This section provides a detailed guide on how to conduct statistical comparisons, from data preparation to result interpretation.
3.1 Data Preparation
Before running any statistical test, it’s important to prepare your data. This involves:
- Data Collection: Gathering the relevant data from reliable sources.
- Data Cleaning: Identifying and correcting errors, inconsistencies, and missing values.
- Data Transformation: Converting the data into a suitable format for analysis (e.g., converting categorical variables into numerical codes).
- Data Organization: Arranging the data in a structured manner, such as a spreadsheet or database.
Proper data preparation is crucial for ensuring the accuracy and reliability of your results. Neglecting this step can lead to biased or misleading conclusions.
3.2 Conducting the Statistical Test
The process of conducting the statistical test involves:
- State the Hypotheses: Define the null and alternative hypotheses.
- Set the Significance Level: Choose a significance level (alpha) to determine the threshold for statistical significance.
- Compute the Test Statistic: Calculate the value of the test statistic using the appropriate formula.
- Determine the P-value: Find the p-value associated with the test statistic.
- Make a Decision: Compare the p-value to the significance level and decide whether to reject or fail to reject the null hypothesis.
Statistical software packages like R, SPSS, and Python can automate these calculations and provide you with the necessary outputs.
3.3 Interpreting the Results
Interpreting the results of a statistical test involves:
- Evaluating the P-value: If the p-value is less than the significance level, you reject the null hypothesis and conclude that there is a statistically significant difference between the groups.
- Considering the Effect Size: Assess the magnitude of the difference between groups. A statistically significant difference may not be practically meaningful if the effect size is small.
- Examining Confidence Intervals: Determine the range of values that is likely to contain the true population parameter. This provides additional information about the precision of your estimate.
It’s important to interpret the results in the context of your research question and consider any limitations of the study.
3.4 Example Walkthrough: Comparing Two Groups Using a T-Test
Let’s walk through an example of comparing two groups using an independent samples t-test. Suppose we want to compare the average weight loss of two groups of people who followed different diet plans.
- Data Preparation: Collect the weight loss data for each group and organize it in a spreadsheet.
- State the Hypotheses:
- Null Hypothesis: There is no difference in the average weight loss between the two diet plans.
- Alternative Hypothesis: There is a difference in the average weight loss between the two diet plans.
- Set the Significance Level: Let’s set the significance level to 0.05.
- Compute the Test Statistic: Use a statistical software package to calculate the t-statistic.
- Determine the P-value: Find the p-value associated with the t-statistic.
- Make a Decision: If the p-value is less than 0.05, we reject the null hypothesis and conclude that there is a statistically significant difference in the average weight loss between the two diet plans.
This example illustrates the process of conducting a statistical comparison from start to finish.
4. Advanced Techniques and Considerations
While basic statistical tests are sufficient for many comparisons, advanced techniques and considerations are sometimes necessary to address more complex scenarios. This section explores some of these advanced topics.
4.1 Analysis of Variance (ANOVA)
ANOVA is used to compare the means of three or more groups. It tests whether there is a significant difference between at least two of the group means. ANOVA is an extension of the t-test for multiple groups.
4.2 Regression Analysis
Regression analysis is used to model the relationship between a dependent variable and one or more independent variables. It can be used to predict the value of the dependent variable based on the values of the independent variables. Regression analysis is useful for understanding the factors that influence a particular outcome.
4.3 Non-Parametric Tests
Non-parametric tests are used when the data does not meet the assumptions of parametric tests (e.g., normality). These tests are based on ranks or signs rather than the actual values of the data. Examples of non-parametric tests include the Mann-Whitney U test, Wilcoxon signed-rank test, and Kruskal-Wallis test.
4.4 Multiple Comparisons
When conducting multiple comparisons, there is an increased risk of making a Type I error (falsely rejecting the null hypothesis). To address this issue, various methods can be used to adjust the significance level, such as the Bonferroni correction or the Benjamini-Hochberg procedure.
4.5 Effect Size Measures
Effect size measures provide information about the magnitude of the difference between groups. Common effect size measures include Cohen’s d, eta-squared, and Pearson’s r. These measures are useful for determining the practical significance of a statistical finding.
5. Common Pitfalls to Avoid
Even with a solid understanding of statistical methods, it’s easy to make mistakes that can compromise the validity of your results. This section highlights some common pitfalls to avoid when comparing values statistically.
5.1 Ignoring Assumptions of Statistical Tests
Each statistical test has its own assumptions about the data. Ignoring these assumptions can lead to inaccurate results. For example, the t-test assumes that the data is normally distributed and has equal variances. If these assumptions are not met, the results of the t-test may be unreliable.
5.2 Misinterpreting P-values
The p-value is the probability of observing results as extreme as, or more extreme than, the data, assuming the null hypothesis is true. It does not measure the probability that the null hypothesis is true or false. Misinterpreting p-values can lead to incorrect conclusions.
5.3 Confusing Statistical Significance with Practical Significance
A statistically significant result is not necessarily practically significant. A small effect size may be statistically significant if the sample size is large, but it may not be meaningful in a real-world context. It’s important to consider both statistical and practical significance when interpreting the results of a statistical test.
5.4 Data Dredging
Data dredging, also known as p-hacking, involves conducting multiple statistical tests and selectively reporting the ones that are statistically significant. This can lead to false positives and unreliable results. To avoid data dredging, it’s important to have a clear research question and to pre-specify your analysis plan before collecting data.
5.5 Ignoring Confounding Variables
Confounding variables are factors that can influence both the independent and dependent variables, leading to spurious associations. Ignoring confounding variables can result in incorrect conclusions about the relationship between the variables of interest. To address this issue, it’s important to identify and control for potential confounding variables in your analysis.
6. Tools and Resources for Statistical Comparison
Fortunately, there are many tools and resources available to help you conduct statistical comparisons effectively. This section provides an overview of some of the most useful tools and resources.
6.1 Statistical Software Packages
Statistical software packages can automate the calculations and provide you with the necessary outputs for conducting statistical comparisons. Some popular statistical software packages include:
- R: A free and open-source statistical computing environment.
- SPSS: A commercial statistical software package.
- SAS: A commercial statistical software package.
- Python: A versatile programming language with libraries for statistical analysis, such as NumPy, SciPy, and Pandas.
Each software package has its own strengths and weaknesses, so it’s important to choose the one that best meets your needs.
6.2 Online Calculators
Online calculators can be used to quickly perform simple statistical calculations. These calculators are useful for verifying the results of your own calculations or for conducting preliminary analyses. Many websites offer free online statistical calculators.
6.3 Statistical Textbooks and Guides
Statistical textbooks and guides provide detailed explanations of statistical concepts and methods. These resources are useful for learning about statistical comparison and for understanding the theory behind the statistical tests.
6.4 Online Courses and Tutorials
Online courses and tutorials can provide you with hands-on training in statistical comparison. These resources are useful for developing your skills and for learning how to apply statistical methods to real-world problems. Platforms like Coursera, edX, and Udemy offer a wide range of statistical courses.
6.5 Statistical Consulting Services
If you need assistance with a complex statistical problem, you may want to consider hiring a statistical consultant. Statistical consultants can provide expert advice and guidance on all aspects of statistical analysis.
7. Real-World Applications of Statistical Comparison
Statistical comparison is used in a wide range of fields to make informed decisions and draw meaningful conclusions. This section highlights some real-world applications of statistical comparison.
7.1 Medical Research
In medical research, statistical comparison is used to compare the effectiveness of different treatments, to identify risk factors for diseases, and to evaluate the accuracy of diagnostic tests. For example, clinical trials often use t-tests or ANOVA to compare the outcomes of patients who receive a new treatment versus a placebo.
7.2 Marketing and Advertising
In marketing and advertising, statistical comparison is used to compare the effectiveness of different marketing campaigns, to identify target markets, and to evaluate customer satisfaction. For example, A/B testing uses statistical tests to compare the performance of two versions of a website or advertisement.
7.3 Education
In education, statistical comparison is used to compare the performance of different teaching methods, to evaluate the effectiveness of educational programs, and to identify students who need extra support. For example, t-tests can be used to compare the test scores of students who receive different types of instruction.
7.4 Environmental Science
In environmental science, statistical comparison is used to compare the levels of pollutants in different locations, to evaluate the impact of environmental policies, and to monitor changes in ecosystems. For example, ANOVA can be used to compare the water quality of different lakes or rivers.
7.5 Business and Finance
In business and finance, statistical comparison is used to compare the performance of different investments, to identify trends in the market, and to evaluate the effectiveness of business strategies. For example, regression analysis can be used to predict the future performance of a stock based on historical data.
8. Illustrative Examples of Statistical Comparison
To further illustrate the concepts and techniques discussed in this guide, this section provides several illustrative examples of statistical comparison.
8.1 Example 1: Comparing the Sales Performance of Two Products
A company wants to compare the sales performance of two products, A and B. They collect data on the monthly sales of each product for a period of one year. To compare the sales performance of the two products, they can use an independent samples t-test.
- Data Preparation: Collect the monthly sales data for each product and organize it in a spreadsheet.
- State the Hypotheses:
- Null Hypothesis: There is no difference in the average monthly sales between the two products.
- Alternative Hypothesis: There is a difference in the average monthly sales between the two products.
- Set the Significance Level: Let’s set the significance level to 0.05.
- Compute the Test Statistic: Use a statistical software package to calculate the t-statistic.
- Determine the P-value: Find the p-value associated with the t-statistic.
- Make a Decision: If the p-value is less than 0.05, we reject the null hypothesis and conclude that there is a statistically significant difference in the average monthly sales between the two products.
8.2 Example 2: Comparing the Effectiveness of Two Training Programs
An organization wants to compare the effectiveness of two training programs, X and Y. They randomly assign employees to participate in either training program X or training program Y. After the training programs, they administer a test to assess the employees’ knowledge and skills. To compare the effectiveness of the two training programs, they can use an independent samples t-test.
- Data Preparation: Collect the test scores for each employee and organize it in a spreadsheet.
- State the Hypotheses:
- Null Hypothesis: There is no difference in the average test scores between the two training programs.
- Alternative Hypothesis: There is a difference in the average test scores between the two training programs.
- Set the Significance Level: Let’s set the significance level to 0.05.
- Compute the Test Statistic: Use a statistical software package to calculate the t-statistic.
- Determine the P-value: Find the p-value associated with the t-statistic.
- Make a Decision: If the p-value is less than 0.05, we reject the null hypothesis and conclude that there is a statistically significant difference in the average test scores between the two training programs.
8.3 Example 3: Comparing the Customer Satisfaction Ratings of Three Companies
A market research firm wants to compare the customer satisfaction ratings of three companies, A, B, and C. They collect data on the customer satisfaction ratings for each company. To compare the customer satisfaction ratings of the three companies, they can use ANOVA.
- Data Preparation: Collect the customer satisfaction ratings for each company and organize it in a spreadsheet.
- State the Hypotheses:
- Null Hypothesis: There is no difference in the average customer satisfaction ratings among the three companies.
- Alternative Hypothesis: There is a difference in the average customer satisfaction ratings among the three companies.
- Set the Significance Level: Let’s set the significance level to 0.05.
- Compute the Test Statistic: Use a statistical software package to calculate the F-statistic.
- Determine the P-value: Find the p-value associated with the F-statistic.
- Make a Decision: If the p-value is less than 0.05, we reject the null hypothesis and conclude that there is a statistically significant difference in the average customer satisfaction ratings among the three companies.
9. Case Studies
Examining real-world case studies can provide valuable insights into how statistical comparison is applied in practice. This section presents several case studies that illustrate the use of statistical comparison in different contexts.
9.1 Case Study 1: Comparing the Effectiveness of Two Drugs for Treating Hypertension
A pharmaceutical company conducted a clinical trial to compare the effectiveness of two drugs, X and Y, for treating hypertension. Patients with hypertension were randomly assigned to receive either drug X or drug Y. After a period of several weeks, the researchers measured the blood pressure of each patient. To compare the effectiveness of the two drugs, they used an independent samples t-test.
The results of the t-test showed that the blood pressure of patients who received drug X was significantly lower than the blood pressure of patients who received drug Y. This suggests that drug X is more effective than drug Y for treating hypertension.
9.2 Case Study 2: Comparing the Performance of Two Investment Strategies
An investment firm wants to compare the performance of two investment strategies, A and B. They track the returns of each investment strategy for a period of several years. To compare the performance of the two investment strategies, they used a paired samples t-test.
The results of the t-test showed that the returns of investment strategy A were significantly higher than the returns of investment strategy B. This suggests that investment strategy A is more effective than investment strategy B.
9.3 Case Study 3: Comparing the Fuel Efficiency of Three Car Models
A car manufacturer wants to compare the fuel efficiency of three car models, X, Y, and Z. They conduct a series of tests to measure the fuel efficiency of each car model. To compare the fuel efficiency of the three car models, they used ANOVA.
The results of ANOVA showed that there was a statistically significant difference in the fuel efficiency among the three car models. Further analysis revealed that car model X had significantly higher fuel efficiency than car models Y and Z.
10. Frequently Asked Questions (FAQs)
This section provides answers to some frequently asked questions about comparing values statistically.
Q1: What is the difference between a p-value and a significance level?
A: The p-value is the probability of observing results as extreme as, or more extreme than, the data, assuming the null hypothesis is true. The significance level (alpha) is a threshold used to determine whether the p-value is small enough to reject the null hypothesis.
Q2: What is the difference between statistical significance and practical significance?
A: Statistical significance refers to whether the results of a statistical test are likely due to chance. Practical significance refers to whether the results are meaningful in a real-world context.
Q3: What is the difference between a t-test and ANOVA?
A: A t-test is used to compare the means of two groups. ANOVA is used to compare the means of three or more groups.
Q4: What is a non-parametric test?
A: A non-parametric test is a statistical test that does not assume that the data follows a normal distribution. Non-parametric tests are used when the data does not meet the assumptions of parametric tests.
Q5: How do I choose the right statistical test for my data?
A: To choose the right statistical test, you need to consider the type of data, the number of groups, the independence of the data, and the distribution of the data.
Q6: What is effect size?
A: Effect size is a measure of the magnitude of the difference between groups. It provides more information than just whether the difference is statistically significant.
Q7: What is a confidence interval?
A: A confidence interval is a range of values that is likely to contain the true population parameter.
Q8: How can I avoid data dredging?
A: To avoid data dredging, it’s important to have a clear research question and to pre-specify your analysis plan before collecting data.
Q9: What is a confounding variable?
A: A confounding variable is a factor that can influence both the independent and dependent variables, leading to spurious associations.
Q10: Where can I find help with statistical analysis?
A: You can find help with statistical analysis from statistical software packages, online calculators, statistical textbooks and guides, online courses and tutorials, and statistical consulting services.
11. The Role of COMPARE.EDU.VN in Statistical Comparison
COMPARE.EDU.VN plays a crucial role in helping individuals and organizations effectively compare values statistically. We provide a comprehensive platform with resources, tools, and expert guidance to facilitate accurate and informed decision-making.
11.1 Comprehensive Resources
COMPARE.EDU.VN offers a wide range of resources, including articles, guides, and tutorials, that cover various aspects of statistical comparison. These resources are designed to help users understand the concepts, techniques, and tools involved in statistical comparison.
11.2 Tools and Calculators
COMPARE.EDU.VN provides access to statistical calculators and tools that simplify the process of conducting statistical comparisons. These tools enable users to quickly and easily perform calculations and analyses, without requiring advanced statistical expertise.
11.3 Expert Guidance
COMPARE.EDU.VN offers expert guidance and consulting services to help users with complex statistical problems. Our team of statistical experts can provide advice and support on all aspects of statistical analysis, from data preparation to result interpretation.
11.4 User-Friendly Platform
COMPARE.EDU.VN provides a user-friendly platform that makes it easy for users to find and access the resources, tools, and services they need. Our platform is designed to be intuitive and easy to navigate, even for users with limited statistical knowledge.
11.5 Community Support
COMPARE.EDU.VN fosters a community of users who can share their experiences, ask questions, and provide support to each other. Our community forum provides a space for users to connect and collaborate on statistical projects.
12. Conclusion: Making Informed Decisions with Statistical Comparison
Statistical comparison is a powerful tool for making informed decisions and drawing meaningful conclusions from data. By understanding the concepts, techniques, and tools involved in statistical comparison, you can effectively analyze data and gain valuable insights. Remember to carefully consider the type of data, the research question, and the assumptions of the statistical tests when conducting statistical comparisons.
COMPARE.EDU.VN is committed to providing you with the resources, tools, and expert guidance you need to succeed in statistical comparison. Whether you are comparing products, services, ideas, or any other type of data, our platform can help you make informed decisions and achieve your goals.
Visit COMPARE.EDU.VN today to explore our comprehensive resources and tools for statistical comparison. Let us help you unlock the power of data and make confident, data-driven decisions.
Contact Us:
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
Whatsapp: +1 (626) 555-9090
Website: COMPARE.EDU.VN
Ready to make smarter choices? Head over to compare.edu.vn and discover a world of comparisons at your fingertips!
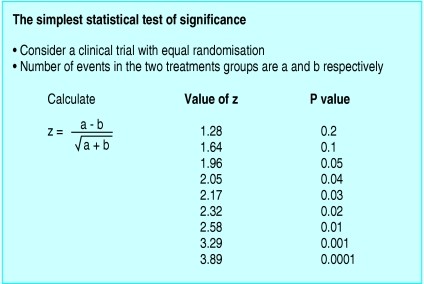Statistical Comparison
13. Glossary of Terms
To ensure clarity and understanding, here’s a glossary of terms commonly used in statistical comparison:
- Alpha (α): The significance level, the probability of rejecting the null hypothesis when it is true.
- Alternative Hypothesis (H1): The hypothesis that states there is a significant difference or effect.
- ANOVA (Analysis of Variance): A statistical test used to compare the means of three or more groups.
- Chi-Square Test: A statistical test used to analyze categorical data and determine if there is a significant association between two variables.
- Confidence Interval (CI): A range of values that is likely to contain the true population parameter with a certain level of confidence.
- Confounding Variable: A variable that influences both the independent and dependent variables, leading to a spurious association.
- Data Dredging (P-Hacking): The practice of selectively reporting statistically significant results from multiple tests.
- Effect Size: A measure of the magnitude of the difference between groups.
- Hypothesis Testing: A statistical method used to make inferences about a population based on a sample of data.
- Mann-Whitney U Test: A non-parametric test used to compare two independent groups when the data is not normally distributed.
- Null Hypothesis (H0): The hypothesis that states there is no significant difference or effect.
- P-value: The probability of observing results as extreme as, or more extreme than, the data, assuming the null hypothesis is true.
- Regression Analysis: A statistical method used to model the relationship between a dependent variable and one or more independent variables.
- Significance Level (α): The probability of rejecting the null hypothesis when it is true, typically set at 0.05.
- Statistical Power: The probability of correctly rejecting the null hypothesis when it is false.
- T-test: A statistical test used to compare the means of two groups.
- Wilcoxon Signed-Rank Test: A non-parametric test used to compare two related groups when the data is not normally distributed.
This glossary will serve as a helpful reference as you navigate the world of statistical comparison.
