Comparing two fractions involves determining which fraction represents a larger or smaller portion of a whole. At COMPARE.EDU.VN, we provide you with a clear understanding of various methods to effectively compare fractions. Master these techniques to easily compare fractional values, understand fraction magnitude and refine your number comparison skills.
Are you struggling to compare fractions effectively? COMPARE.EDU.VN offers in-depth comparison methods and resources to master fraction evaluation. Explore equivalent fractions, visual representations, and decimal conversions to enhance your quantitative reasoning skills.
1. Understanding Fractions and Their Components
Before diving into the methods of comparison, it’s crucial to understand what a fraction represents. A fraction is a part of a whole, consisting of two key components: the numerator and the denominator.
1.1. Defining the Numerator
The numerator is the number above the fraction bar, indicating how many parts of the whole are being considered. For example, in the fraction 3/4, the numerator is 3.
1.2. Defining the Denominator
The denominator is the number below the fraction bar, indicating the total number of equal parts that make up the whole. In the fraction 3/4, the denominator is 4.
Understanding these components is essential for grasping the concept of comparing fractions effectively.
2. Why Comparing Fractions Matters
Comparing fractions is not just a mathematical exercise; it has practical applications in everyday life. Whether you’re following a recipe, managing finances, or making decisions based on proportions, understanding how to compare fractions is invaluable.
2.1. Real-Life Applications
In cooking, you might need to compare 1/3 cup of sugar to 1/4 cup to decide which measurement is greater. In finance, comparing fractions can help you understand investment returns or allocate resources effectively.
2.2. Academic Importance
Beyond practical uses, comparing fractions is a fundamental skill in mathematics. It forms the basis for more advanced concepts such as ratios, proportions, and algebra. A strong understanding of fraction comparison is crucial for academic success.
3. Methods for Comparing Fractions
There are several methods for comparing fractions, each suited to different situations. Let’s explore these methods in detail, providing step-by-step instructions and examples.
3.1. Comparing Fractions with the Same Denominator
The simplest method is when the fractions have the same denominator. In this case, you only need to compare the numerators.
3.1.1. Step-by-Step Instructions
- Check if the denominators of the fractions are the same.
- Compare the numerators. The fraction with the larger numerator is the larger fraction.
- If the numerators are equal, the fractions are equal.
3.1.2. Example
Compare 5/12 and 7/12.
- Both fractions have the same denominator (12).
- Compare the numerators: 5 and 7.
- Since 7 > 5, 7/12 is greater than 5/12.
3.2. Comparing Fractions with the Same Numerator
When fractions have the same numerator but different denominators, the fraction with the smaller denominator is larger.
3.2.1. Step-by-Step Instructions
- Check if the numerators of the fractions are the same.
- Compare the denominators. The fraction with the smaller denominator is the larger fraction.
3.2.2. Example
Compare 3/8 and 3/5.
- Both fractions have the same numerator (3).
- Compare the denominators: 8 and 5.
- Since 5 < 8, 3/5 is greater than 3/8.
This may seem counterintuitive, but remember that the smaller the denominator, the larger the individual parts of the whole.
3.3. Comparing Fractions with Different Numerators and Denominators
When fractions have different numerators and denominators, you need to use more advanced techniques. Here are some common methods: finding a common denominator, cross multiplication, and converting to decimals.
3.3.1. Finding a Common Denominator
This method involves finding a common denominator for both fractions and then comparing the numerators.
3.3.1.1. Step-by-Step Instructions
- Find the least common multiple (LCM) of the denominators. This will be the common denominator.
- Convert each fraction to an equivalent fraction with the common denominator.
- Compare the numerators. The fraction with the larger numerator is the larger fraction.
3.3.1.2. Example
Compare 2/3 and 3/4.
- Find the LCM of 3 and 4. The LCM is 12.
- Convert 2/3 to an equivalent fraction with a denominator of 12: (2/3) * (4/4) = 8/12.
- Convert 3/4 to an equivalent fraction with a denominator of 12: (3/4) * (3/3) = 9/12.
- Compare the numerators: 8 and 9.
- Since 9 > 8, 9/12 (or 3/4) is greater than 8/12 (or 2/3).
3.3.2. Cross Multiplication
Cross multiplication is a quick method for comparing two fractions.
3.3.2.1. Step-by-Step Instructions
- Multiply the numerator of the first fraction by the denominator of the second fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the two products. If the first product is larger, the first fraction is larger. If the second product is larger, the second fraction is larger. If the products are equal, the fractions are equal.
3.3.2.2. Example
Compare 2/5 and 3/7.
- Multiply 2 (numerator of the first fraction) by 7 (denominator of the second fraction): 2 * 7 = 14.
- Multiply 3 (numerator of the second fraction) by 5 (denominator of the first fraction): 3 * 5 = 15.
- Compare the products: 14 and 15.
- Since 15 > 14, 3/7 is greater than 2/5.
3.3.3. Converting to Decimals
Another method is to convert each fraction to a decimal and then compare the decimal values.
3.3.3.1. Step-by-Step Instructions
- Divide the numerator of each fraction by its denominator to convert it to a decimal.
- Compare the decimal values. The fraction with the larger decimal value is the larger fraction.
3.3.3.2. Example
Compare 5/8 and 7/10.
- Convert 5/8 to a decimal: 5 ÷ 8 = 0.625.
- Convert 7/10 to a decimal: 7 ÷ 10 = 0.7.
- Compare the decimal values: 0.625 and 0.7.
- Since 0.7 > 0.625, 7/10 is greater than 5/8.
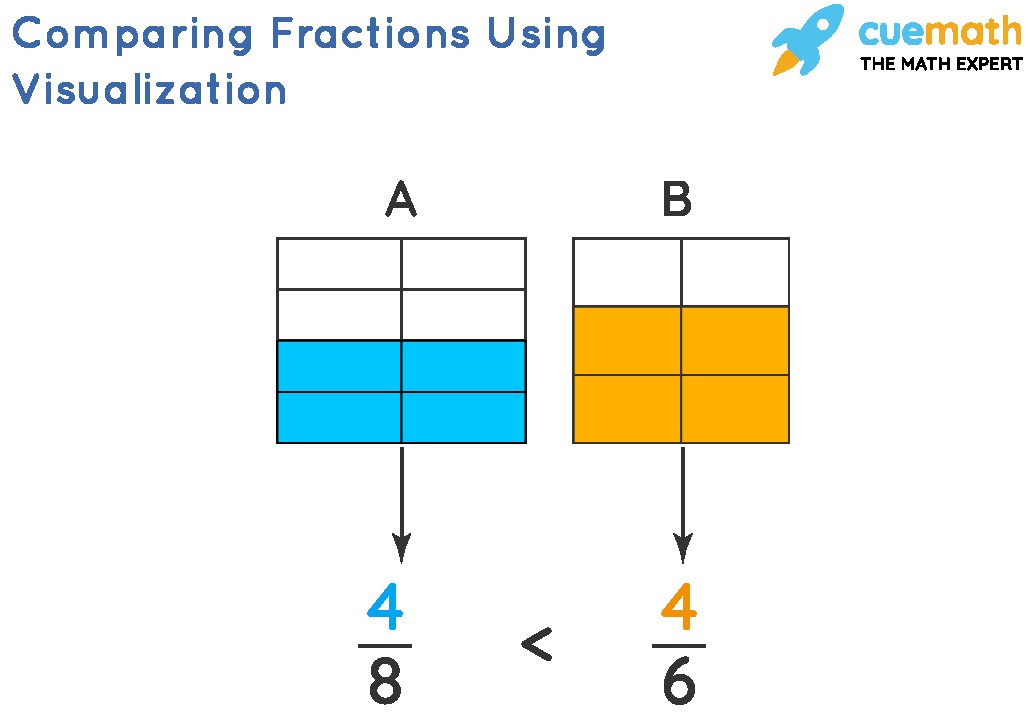
4. Visualizing Fractions
Visual aids can be incredibly helpful for understanding and comparing fractions. Common methods include using fraction bars, pie charts, and number lines.
4.1. Fraction Bars
Fraction bars are rectangular bars divided into equal parts, with different fractions represented by shading a portion of the bar. By visually comparing the shaded areas, you can easily determine which fraction is larger.
4.2. Pie Charts
Pie charts represent the whole as a circle, divided into segments representing fractions. Comparing the sizes of the segments helps visualize the relative size of the fractions.
4.3. Number Lines
Number lines provide a linear representation of fractions. By plotting fractions on a number line, you can see their relative positions and compare their values.
5. Advanced Techniques and Considerations
Beyond the basic methods, there are more advanced techniques and considerations for comparing fractions, especially when dealing with complex scenarios.
5.1. Comparing Mixed Numbers
A mixed number is a combination of a whole number and a fraction (e.g., 3 1/2). To compare mixed numbers, first compare the whole numbers. If the whole numbers are different, the mixed number with the larger whole number is larger. If the whole numbers are the same, compare the fractional parts using one of the methods discussed earlier.
5.2. Comparing Improper Fractions
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 7/4). To compare improper fractions, you can convert them to mixed numbers and then compare as described above, or use the common denominator or cross-multiplication methods.
5.3. Simplifying Fractions Before Comparing
Simplifying fractions before comparing them can make the process easier. To simplify a fraction, divide both the numerator and denominator by their greatest common factor (GCF). For example, 4/6 can be simplified to 2/3 by dividing both numbers by 2.
5.4. Dealing with Negative Fractions
When comparing negative fractions, remember that the fraction closer to zero is larger. For example, -1/4 is larger than -1/2 because -1/4 is closer to zero on the number line.
6. Common Mistakes to Avoid
Comparing fractions can be tricky, and it’s easy to make mistakes. Here are some common pitfalls to avoid:
6.1. Assuming Larger Denominator Means Larger Fraction
It’s a common mistake to assume that a fraction with a larger denominator is always larger. This is only true when the numerators are the same. For example, 1/8 is smaller than 1/4, even though 8 is larger than 4.
6.2. Forgetting to Find a Common Denominator
When comparing fractions with different denominators, it’s essential to find a common denominator before comparing the numerators. Failing to do so can lead to incorrect conclusions.
6.3. Not Simplifying Fractions
Not simplifying fractions can make the comparison process more complicated. Simplifying fractions before comparing can reduce the size of the numbers and make the comparison easier.
6.4. Misunderstanding Negative Fractions
When dealing with negative fractions, it’s important to remember that the fraction closer to zero is larger. Misunderstanding this concept can lead to errors in comparison.
7. Practice Exercises
To solidify your understanding of comparing fractions, here are some practice exercises:
- Compare 3/5 and 4/7 using the common denominator method.
- Compare 5/9 and 7/11 using cross multiplication.
- Compare 2/3 and 0.65 by converting fractions to decimals.
- Order the following fractions from smallest to largest: 1/2, 3/8, 2/5, 5/12.
- Compare the mixed numbers 2 1/4 and 2 2/5.
8. The Role of COMPARE.EDU.VN in Mastering Fraction Comparisons
COMPARE.EDU.VN is dedicated to providing comprehensive, objective comparisons across a wide array of subjects, including mathematics. Our platform simplifies the process of understanding complex concepts by offering clear explanations, step-by-step guides, and practical examples.
8.1. Comprehensive Resources
Our website features a wealth of resources designed to help you master fraction comparisons. From detailed articles and tutorials to interactive quizzes and practice exercises, we offer everything you need to succeed.
8.2. Objective Comparisons
We pride ourselves on providing objective, unbiased comparisons. Our content is thoroughly researched and carefully vetted to ensure accuracy and reliability. You can trust COMPARE.EDU.VN to provide you with the information you need to make informed decisions.
8.3. User-Friendly Interface
Our user-friendly interface makes it easy to navigate our website and find the information you’re looking for. Whether you’re a student, teacher, or lifelong learner, you’ll find our platform intuitive and engaging.
9. Expert Opinions on Fraction Comparison
To provide a well-rounded perspective, we’ve gathered insights from math educators and experts on the importance of mastering fraction comparison.
9.1. Importance in Mathematical Foundation
“Understanding how to compare fractions is a cornerstone of mathematical literacy,” says Dr. Emily Carter, a mathematics professor at the University of California. “It’s essential for building a solid foundation in more advanced math topics like algebra and calculus.”
9.2. Real-World Relevance
“Fractions are everywhere in the real world, from cooking and baking to finance and engineering,” notes Mr. John Davis, a high school math teacher. “Being able to compare fractions accurately is a critical skill for success in many fields.”
9.3. Conceptual Understanding
“It’s not enough to just memorize the rules for comparing fractions,” adds Ms. Sarah Lee, an elementary school teacher. “Students need to develop a conceptual understanding of what fractions represent and how they relate to each other. Visual aids and hands-on activities can be incredibly helpful.”
10. Conclusion: Empowering Fraction Comparison Skills
Mastering How To Compare Two Fractions is a fundamental skill with wide-ranging applications. By understanding the basic concepts, exploring different comparison methods, and practicing regularly, you can develop confidence and competence in this area.
COMPARE.EDU.VN is here to support you every step of the way. Our comprehensive resources, objective comparisons, and user-friendly interface make it easy to master fraction comparisons and other essential math skills.
Don’t let fraction comparisons intimidate you. Visit COMPARE.EDU.VN today and unlock your mathematical potential. For further inquiries, reach out to us at 333 Comparison Plaza, Choice City, CA 90210, United States. You can also contact us via Whatsapp at +1 (626) 555-9090. Start your journey to mathematical mastery now!
11. Frequently Asked Questions (FAQs)
11.1. What Does Comparing Fractions Mean?
Comparing fractions means determining which fraction is larger or smaller than another. It helps in understanding the relative size or value of different fractional parts. Like whole numbers, fractions can be compared using the symbols <, >, and =.
11.2. How Do You Compare Fractions with the Same Denominator?
When fractions have the same denominator, compare their numerators. The fraction with the larger numerator is the larger fraction. If the numerators are equal, the fractions are equal.
11.3. What Is the Rule When Comparing Fractions with the Same Numerator?
When fractions have the same numerator, the fraction with the smaller denominator is larger. This is because the whole is divided into fewer parts, making each part larger.
11.4. What Are Equivalent Fractions?
Equivalent fractions are fractions that represent the same value, even though they have different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions.
11.5. What Is the Easiest Way of Comparing Fractions?
The easiest way to compare fractions is often to convert them to decimals. This allows for a straightforward comparison using decimal values.
11.6. Why Do We Need to Compare Fractions?
Comparing fractions is essential for various real-life scenarios, such as cooking, finance, and problem-solving. It also builds a strong foundation for more advanced mathematical concepts.
11.7. How to Compare Fractions with Different Denominators?
To compare fractions with different denominators, find the least common multiple (LCM) of the denominators and convert each fraction to an equivalent fraction with the common denominator. Then, compare the numerators.
11.8. Can You Use Cross Multiplication to Compare Fractions?
Yes, cross multiplication is a quick method. Multiply the numerator of one fraction by the denominator of the other, and compare the products. The larger product indicates the larger fraction.
11.9. What Should I Do if I Encounter Negative Fractions?
With negative fractions, remember that the fraction closer to zero is larger. For instance, -1/4 is larger than -1/2 because it is closer to zero on the number line.
11.10. Where Can I Find More Resources on Comparing Fractions?
You can find more resources, detailed tutorials, and practice exercises on comparing fractions at compare.edu.vn. Our platform is designed to provide comprehensive support for mastering this skill.