Are you looking for a definitive way to compare two curves statistically? COMPARE.EDU.VN offers a streamlined approach using a modified Chi-squared method to establish statistical significance, accommodating single measurements with known standard deviations or multiple measurements averaged to produce means and standard errors. This article provides a comprehensive guide, optimized for search engines, on How To Compare Two Curves Statistically. Learn the techniques to validate the differences and ensure the integrity of your findings through rigorous curve comparison.
1. Introduction: Understanding Curve Comparison
In various fields, especially biomedical sciences, the analysis of curves representing experimental outputs as functions of independent parameters is critical. While some phenomena are easily described by functions reducible to fit parameters, many complex biological functions require a robust method to determine the statistical significance between curves. Determining how to compare two curves statistically can be challenging. This article introduces a spreadsheet-based method, leveraging the Chi-squared test with corrections for small sample sizes, to calculate p-values, addressing the null hypothesis that measurements were sampled from the same parent population at each point. This statistical curve comparison ensures accuracy and reliability in your research.
2. Challenges in Comparing Arbitrary Curves
Comparing arbitrary curves involves testing if two curves, like those in Fig 1, were sampled from the same population, without assumptions about how curve values change. Common methods like two-factor ANOVA often fall short. The key is comparing the total sum of squared differences between curves to the expected distribution from random sampling, assuming the null hypothesis is true. This article demonstrates how to compare two curves statistically, providing the tools to overcome these challenges.
3. The Modified Chi-Squared Method: A Detailed Overview
The Chi-squared method is used to determine the statistical significance between any pair of arbitrary curves. This method builds upon the Chi-squared test for goodness of fit, with an essential correction for the deviation from normality that arises with small to moderate sample sizes, typical in biomedical research. This approach calculates an overall p-value for the null hypothesis that, at every value of X, the measurements for two curves were sampled from the same parent population.
3.1. Key Components of the Method
This modified Chi-squared method involves:
- Calculating Chi-squared values for each pair of points.
- Correcting for non-normality using t-distributions.
- Summing the corrected Chi-squared values to obtain an overall statistic.
- Determining an overall p-value for the comparison of the curves.
3.2. Benefits of This Approach
- Accuracy: This method accurately assesses statistical significance, even with small sample sizes.
- Versatility: Applicable to any pair of curves, regardless of their functional form.
- Ease of Use: Implemented via a simple spreadsheet, making it accessible to researchers without extensive statistical backgrounds.
- False Positive Rate Control: Maintains a consistent false positive rate (Type I error) at the chosen significance level (e.g., 0.05).
- Post Hoc Analysis: Provides a post hoc test for calculating p-values for individual pairs of points, corrected for multiple comparisons, helping to pinpoint which points contribute most to the overall statistical significance.
4. Methodological Framework: A Step-by-Step Guide
The method relies on the Chi-squared test to compare the differences between the curves to a distribution of expected differences. Here is the mathematical foundation for this approach.
4.1. Chi-Squared Comparison of Two Means
The Chi-squared (χ2) probability distribution compares categorical data, with applications in continuous data, especially in regression and curve fitting. The general form is:
χi2 = (Oi - Ei)^2 / σi^2
Where Oi is the observed value, Ei is the expected value, and σi is the standard deviation.
4.2. Two Scenarios for Curve Comparison
This section details two scenarios for comparing curves, each tailored to the available data and experimental conditions. Understanding these scenarios is crucial for selecting the appropriate statistical approach and ensuring accurate and meaningful results.
4.2.1. Scenario 1: Single Measurement with Known Standard Deviation
This scenario applies when each point in the curve has been measured in a single experiment, and the standard deviation (σi) is known from previous measurements. When comparing two measurements, Oij (where j = dataset a or b), the χi2 takes the form:
χi2 = (Oia - Oib)^2 / σidiff^2
Where:
σidiff = sqrt(σia^2 + σib^2)
This calculation uses propagation of errors to determine the standard deviation of the difference.
4.2.2. Scenario 2: Multiple Measurements, Mean, and Standard Error
This scenario applies when each point is measured in N independent experiments, allowing representation as a mean (Oi) and standard error (SEi). When comparing a pair of such means, the χi2 takes the form:
χi2 = (Oia - Oib)^2 / SEidiff^2
Where:
SEidiff = sqrt(SEia^2 + SEib^2)
And:
SEij = σij / sqrt(Nij)
4.3. Correcting for Small N Using the t-Distribution
The Chi-squared formalism assumes a Gaussian distribution around each point. However, this is only true with large N. For N ≤ 20, deviations from normality are significant. To correct for small N, we use t-distributions to determine a corrected χ2.
4.3.1. Steps for Correction
- Calculate t-value:
ti = (Oia - Oib) / SEidiff - Determine probability using t-distribution:
Use t and dFt (degrees of freedom for t) to find pi. - Calculate corrected Chi-squared:
Use pi and dF = 1 to calculate χcorr,i2.
4.4. Calculating Overall Statistical Significance
To determine the overall p-value for the difference between curves, the corrected χ2 values are summed:
χsum2 = Σ χcorr,i2
The overall p-value is then determined using a χ2 calculator with dF = M, where M is the number of pairs of points:
χsum2 and dFcurves(M) → χ2-distribution poverall
4.5. Defining the Null Hypothesis and p-Value
The null hypothesis states that each pair of measurements Oia and Oib collected at the same X value were sampled from the same parent population at that point.
5. Practical Implementation: Using Spreadsheets for Analysis
To facilitate the application of the modified Chi-squared method, this section provides detailed instructions on how to implement the calculations in Microsoft Excel. A spreadsheet with these functions coded as described below is included in S1 File. The spreadsheet is designed to accommodate the two scenarios discussed earlier:
- Scenario 1: N = 1 measurement at each X, with a known SD (labelled “N = 1 with SD”)
- Scenario 2: N > 1 measurements at each X which are used to calculate mean and SE (labelled “N>1, mean and SE”)
5.1. Excel Setup for Scenario 1: Single Measurement with Known SD
This setup guides you through calculating individual χ2 values when you have one measurement at each X-value and a known standard deviation.
- Column Designations: Match the columns to the S1 File labelled “N = 1 with SD”.
- Column A: Enter Xi, the X-values for the two curves, a and b.
- Column B: Enter Oia (Measured value of Y for point i, Curve a).
- Column C: Enter SDia (SD of point i, Curve a).
- Column D: Enter Oib (Curve b).
- Column E: Enter SDib (Curve b).
- Column G: Calculate the absolute difference between the means using the formula:
[= ABS(Di-Bi)]. - Column H: Calculate the standard deviation of the difference using:
[= SQRT(Ci^2+Ei^2)]. - Column I: Calculate the individual Chi-squared values using:
[= (Gi/Hi)^2].
5.2. Excel Setup for Scenario 2: Multiple Measurements, Mean, and SE
This setup is for when you have multiple measurements per point, allowing you to calculate means and standard errors.
- Raw Measurements: Enter Yij = a raw measurements for curve a in rows, one row per X-value.
- Calculate Mean: Calculate the mean of point i in curve j = a using:
[= AVERAGE(Y1a:YNa)]where N is Nia. - Calculate Standard Deviation: Calculate the SD of point i in curve j = a using:
[= STD.S(Y1a:YNa)]where N is Nia. - Calculate Number of Measurements: Determine the number of measurements for each point i in curve j = a using:
[= COUNT(Y1a:Yalla)]. - Calculate Standard Error: Calculate the SE of point i in curve j = a using:
[= STD.S(Y1a:YNa)/SQRT(N)]where N is Nia. - Repeat for Curve b: Repeat the above steps for curve b to get Oib, SDib, Nib, and SEib.
- Paste Values: Paste these calculated values into the worksheet for Chi-squared calculation.
5.3. Calculating Individual Chi-Squared Values with N>1, Mean, and SE
Follow these steps to calculate individual Chi-squared values in Excel when you have multiple measurements per point and have calculated the mean and standard error.
- Column Designations: Match the columns to the S1 File labelled “N>1 with mean and SE”.
- Column A: Enter Xi, the X-values for the two curves, a and b.
- Column B: Enter Oia (Mean of Y for point i, Curve a).
- Column C: Enter SDia (SD of point i, Curve a). (SD is not directly used in the calculations)
- Column D: Enter Nia (Number of measurements for point i, Curve a).
- Column E: Enter SEia (SE of point i, Curve a).
- Column F: Enter Oib (Curve b).
- Column G: Enter SDib (SD of point i, Curve b).
- Column H: Enter Nib (Curve b).
- Column I: Enter SEib (SE of point i, Curve b).
- Column K: Calculate the absolute difference between the means using:
[= ABS(Fi-Bi)]. - Column L: Calculate the standard error of the difference using:
[= SQRT(Ei^2+Ii^2)]. - Column M: Calculate the t-value for the ith pair of points using:
[= Ki/Li]. - Column N: Determine N for dF calculation. If the number of data points is unequal, choose the smaller of the two N values using: `[= IF(Hi
- Column O: Calculate dF for t-calculation using:
[= 2*Ni-2]. - Column P: Calculate the probability from t and dF using:
[= T.DIST.2T(Mi,Oi)]. - Column Q: Calculate the corrected χi2 using the probability in Col P and dF = 1 with:
[= CHISQ.INV.RT(Pi,1)].
5.4. Calculating the Overall p-Value in Excel Using Chi-Squared
To calculate the overall p-value in Excel using the Chi-squared method, follow these instructions based on the scenario you are using.
Scenario 1: N = 1 with SD
In this scenario, “Col X” below refers to Col L, and “Col Y” refers to Col I.
Scenario 2: SE from Multiple Measurements
In this scenario, “Col X” below refers to Col T, and “Col Y” refers to Col Q.
- Col X, Cell 2: Calculate the sum of χi2 using:
[= SUM(Y3:Ym)]where m is the row containing the last pair of points. - Col X, Cell 3: Determine dF for χi2 = M, the number of pairs of points, using:
[= COUNT(Y3:Ym)]. - Col X, Cell 4: Calculate the overall p-value for the comparison of the two curves using the sum of χ2 and dF with:
[= 1-CHISQ.DIST(X2,X3,TRUE)].
6. Validation Through Simulation
To validate the accuracy and reliability, the modified Chi-squared method, including the correction for deviation from normality, and the choices for degrees of freedom, simulations of 6,000 pairs of curves were conducted. These simulations tested datasets with 1, 3, and 10 measurements per point (N) and with 3 or 10 points per curve (M).
6.1. Simulation Results
The simulation results, shown in Fig 2, demonstrate that the method accurately calculates p-values and Chi-squared values. The observed p-value frequencies and Chi-squared distributions match the expected distributions, confirming the method’s validity. The simulations confirm that the modified Chi-squared method effectively controls the false positive rate (Type I error) at the chosen significance level, even with small sample sizes.
7. Post Hoc Analysis: Identifying Key Points of Difference
The p-values determined for pairs of points calculated at each value of X using the t-test (Col P, above) enable the post hoc determination of which pairs of points contribute most to the overall difference between the curves.
7.1. Bonferroni Correction for Multiple Comparisons
To maintain statistical rigor, a correction for multiple comparisons is essential. The Bonferroni correction provides a stringent yet straightforward method for calculating a corrected cutoff for statistical significance:
αcorr = αoverall / M
Where αoverall is the desired total Type I error rate (typically 0.05), and M is the number of pairs of points being compared.
7.2. Interpreting Post Hoc Results
Using the Bonferroni-corrected cutoff, one can identify the specific points where the differences between the curves are statistically significant. However, the power of the χ2 method lies in its ability to identify a highly significant difference between curves even when none of the individual point differences rise to the level of significance.
8. Addressing Multiple Pairwise Comparisons
In studies requiring more than one pairwise comparison between curves, such as comparing multiple curves to a control, the χ2 method remains applicable but necessitates a correction for multiple comparisons between curves.
8.1. Applying the Bonferroni Correction
The Bonferroni correction to α, the cutoff for statistical significance, is again appropriate and statistically robust:
αcorr = αoverall / Number of comparisons
This ensures that the overall Type I error rate is maintained at the desired level (e.g., 0.05) across all comparisons.
9. Real-World Application: Analyzing Receptor Heterodimerization
To demonstrate the practical application, we apply the Chi-squared method to a previously published dataset detailing the heterodimerization of mutants of the receptor FGFR3. The heterodimerization of the receptor tyrosine kinase FGFR3 with two pathogenic mutants, A391E and G380R, was characterized. Experimentally, we measured autophosphorylation of the receptors as functions of ligand concentration, both in the presence and absence of enzymatically inactive truncated FGFR3, called ECTMWT-1.
9.1. Data Analysis and Results
We applied the modified χ2 method to the three pairs of curves. All pairwise comparisons are highly significant and give overall p-values of less than 1×10-6. The significance of each individual pair of points is calculated using a 2-sample t-test as described.
9.2. Comparative Analysis of Inhibition
When the degree to which each sequence, WT, A391E, and G380R, is inhibited by the enzymatically inactive construct was compared, the curves appeared superficially similar. The Chi-squared method was initially developed to address whether these curves are significantly different, however the correction for the deviation from normality was not applied at that time. Here, we reanalyze the three comparisons with the fully developed Chi-squared method.
10. Demonstrative Analysis: Comparing Relative Activation Curves
The Chi-squared method is further illustrated through an analysis of relative activation curves, derived from the ratio of receptor activation with and without ECTMwt.
10.1. Modified Chi-Squared Method Results
Based on this method, we conclude that there is a statistically significant difference between the inhibition of wild type versus the G380R mutant. In the other comparisons, there is no significant difference. This demonstrates the importance of using a statistically sound method to identify real differences between curves.
10.2. Data and Calculations
We provide the relative activation data plotted in Fig 4B for wild type FGFR3 and the G380R mutant, along with the intermediate Chi-squared calculations. These example data and calculation results are provided for users to validate any spreadsheet or coded application of the modified Chi-squared method.
10.3. Example Data and Calculations
In Table 1, we provide the relative activation data that is plotted in panel Fig 4B for wild type FGFR3 and the G380R mutant. In Table 2, we provide the intermediate Chi-squared calculations outlined above. These example data and calculation results are provided for users to validate any spreadsheet or coded application of the modified Chi-squared method.
Table 1. Example Data from the Analysis Shown in Fig 4B
| Relative activation of wild type and G380R mutant receptors | |||||||
|---|---|---|---|---|---|---|---|
| Wild type FGFR3 | G380R Mutant FGFR3 | ||||||
| Ligand (nM) | Mean | SD | N | SE | Mean | SD | N |
| 0 | 0.515 | 0.212 | 3 | 0.122 | 1.166 | 0.392 | 3 |
| 5 | 0.309 | 0.155 | 3 | 0.089 | 0.822 | 0.297 | 3 |
| 25 | 0.149 | 0.111 | 3 | 0.064 | 0.708 | 0.265 | 3 |
| 50 | 0.205 | 0.126 | 3 | 0.073 | 0.673 | 0.256 | 3 |
| 125 | 0.151 | 0.111 | 3 | 0.064 | 0.390 | 0.177 | 3 |
| 500 | 0.195 | 0.123 | 3 | 0.071 | 0.331 | 0.161 | 3 |
| 1250 | 0.338 | 0.163 | 3 | 0.094 | 0.241 | 0.136 | 3 |
| 2500 | 0.415 | 0.184 | 3 | 0.106 | 0.395 | 0.179 | 3 |
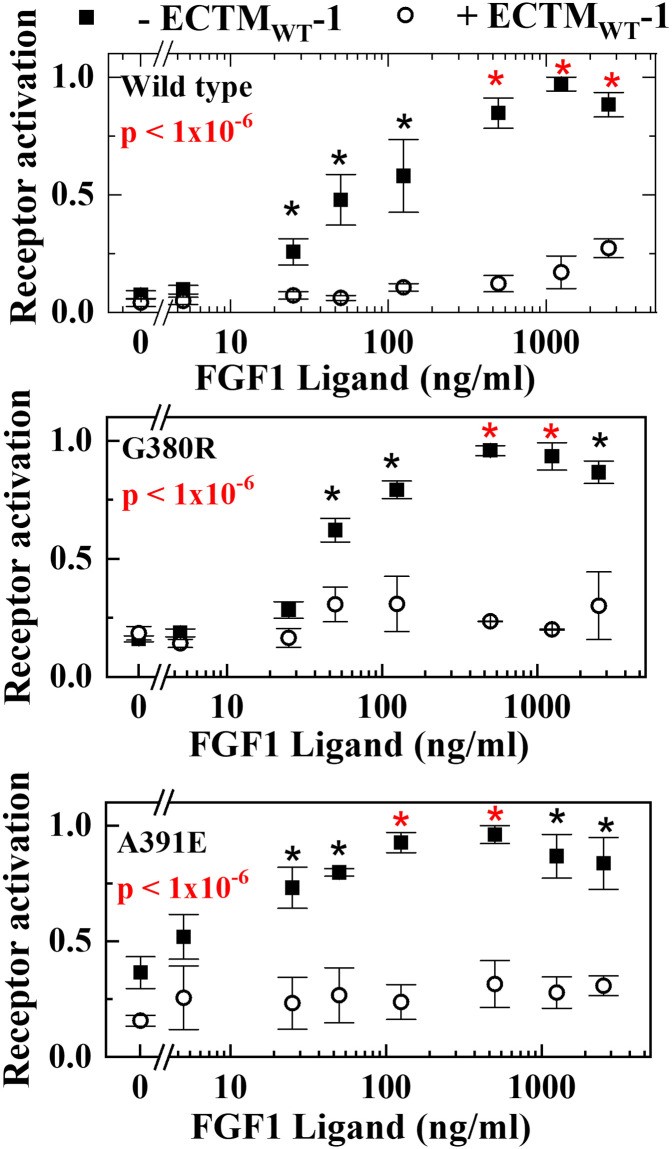
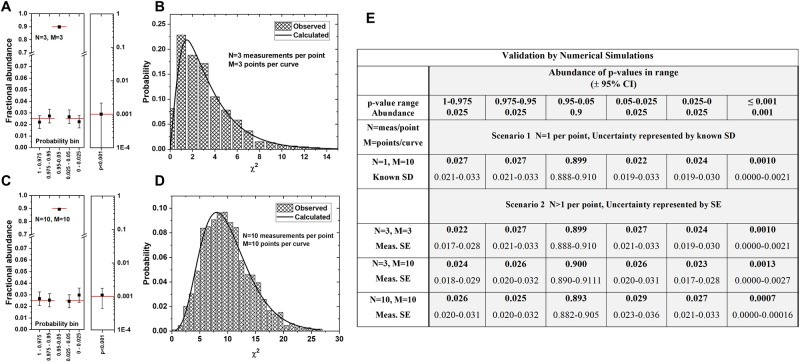
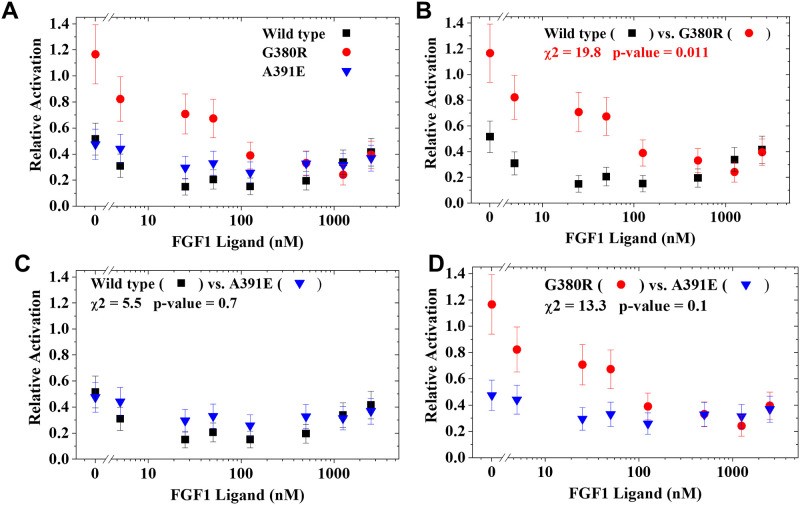
Table 2. Example Calculations of the Chi-squared Test Applied to the Two Curves Shown in Fig 4B and in Table 1
| χ2 based comparison of wild type versus G380R mutant curves | |||||||
|---|---|---|---|---|---|---|---|
| Ligand (nM) | Difference | SE Diff | t-value | N/pt | dF | P-value | χ2 |
| 0 | 0.651 | 0.257 | 2.527 | 3 | 4 | 0.065 | 3.409 |
| 5 | 0.513 | 0.194 | 2.652 | 3 | 4 | 0.057 | 3.627 |
| 25 | 0.558 | 0.166 | 3.363 | 3 | 4 | 0.028 | 4.814 |
| 50 | 0.468 | 0.165 | 2.841 | 3 | 4 | 0.047 | 3.952 |
| 125 | 0.238 | 0.121 | 1.972 | 3 | 4 | 0.12 | 2.419 |
| 500 | 0.136 | 0.117 | 1.161 | 3 | 4 | 0.31 | 1.029 |
| 1250 | 0.097 | 0.123 | 0.791 | 3 | 4 | 0.47 | 0.514 |
| 2500 | 0.020 | 0.148 | 0.135 | 3 | 4 | 0.90 | 0.016 |
| Sum of χ2 | 19.8 | ||||||
| dF | 8 | ||||||
| p-value | 0.011 |
11. Important Considerations and Limitations
A limitation of this modified Chi-squared method for comparing curves is that the two curves must have data measured at the same values of X to enable pairwise comparisons. Data from one curve without corresponding data at the same X in the other must be ignored, or an appropriate extrapolation of data and uncertainty must be carried out using nearby points.
11.1. Data Requirements and Assumptions
- Paired Data: The curves must be measured at the same X values.
- Normality: The data at each value of X must approach a Gaussian distribution for large N.
- Non-Zero SD/SE: SD/SE values cannot be zero for both curves being compared.
11.2. Addressing Non-Gaussian Data
Non-Gaussian data can be log-transformed, which frequently gives a normal distribution, when the linear data are not Gaussian. Use of log transformed data often provides a rigorous solution to the problem of non-normal data.
12. Conclusion: Empowering Accurate Curve Comparisons
We present a simple modified Chi-squared based method to determine the statistical significance of the difference between two arbitrary curves. This method can be performed using a spreadsheet program and is applicable to any pair of X-Y datasets in which the X-values are matched in pairs and in which the uncertainties of the individual points are known or have been measured in independent experiments. A functional Excel spreadsheet is provided as S1 File.
13. FAQs: Your Questions Answered
Q1: What is the primary advantage of the modified Chi-squared method?
A: The primary advantage is its ability to accurately assess statistical significance between curves, even with small sample sizes, by correcting for deviations from normality.
Q2: Can this method be used for any type of curve?
A: Yes, this method is versatile and can be applied to any pair of curves, regardless of their functional form.
Q3: What if my data does not follow a Gaussian distribution?
A: Non-Gaussian data can often be normalized by log-transformation, which is a common practice in statistical analysis.
Q4: How does the Bonferroni correction help in post hoc analysis?
A: The Bonferroni correction helps control the false positive rate when performing multiple comparisons, ensuring that the identified differences are statistically significant.
Q5: What should I do if the SD/SE values are zero for both curves?
A: You must assume a minimal nonzero value of SD/SE, based on an average uncertainty across many such measurements.
Q6: Is the Excel spreadsheet customizable for different datasets?
A: Yes, the Excel spreadsheet is designed to be flexible and customizable, allowing you to input your own data and adjust the calculations as needed.
Q7: How can I validate my implementation of the method?
A: The example data and calculations provided in the tables allow you to validate your implementation of the modified Chi-squared method.
Q8: What if I have more than two curves to compare?
A: The method can be extended to multiple pairwise comparisons, but you must apply a correction for multiple comparisons, such as the Bonferroni correction.
Q9: What level of statistical background is required to use this method?
A: While a basic understanding of statistics is helpful, the method is designed to be accessible to researchers without extensive statistical backgrounds, especially with the provided Excel spreadsheet.
Q10: Where can I find additional resources and support for using this method?
A: COMPARE.EDU.VN provides comprehensive resources and support for using this method, including detailed instructions, example datasets, and expert guidance.
14. Take Action: Start Comparing Your Curves Today
Ready to start comparing your curves with confidence? Visit COMPARE.EDU.VN today for more information, resources, and tools to help you make informed decisions. Contact us at:
- Address: 333 Comparison Plaza, Choice City, CA 90210, United States
- WhatsApp: +1 (626) 555-9090
- Website: COMPARE.EDU.VN
Take the guesswork out of curve comparison. Let COMPARE.EDU.VN help you achieve accurate, reliable, and statistically sound results.
This content is designed to be shared, saved, and pinned by audiences seeking to compare various options. It encourages users to visit compare.edu.vn for further comparisons and aims to inspire well-informed decision-making based on detailed comparison information.