How To Compare The Spread Of Data Effectively

COMPARE.EDU.VN explains How To Compare The Spread Of Data effectively using range, variance, standard deviation, and interquartile range (IQR). By understanding these measures, you can gain insights into the variability within a dataset, identify outliers, and make more informed decisions. Explore data distribution, data variability, and statistical analysis.

1. Understanding Data Spread: Why It Matters

Data spread, also known as dispersion or variability, is a fundamental concept in statistics that describes how data points are distributed around a central value. While measures of central tendency, such as the mean, median, and mode, provide a single value summarizing the “typical” data point, they don’t tell the whole story. Understanding data spread is crucial because it reveals the degree of consistency or inconsistency within a dataset.

Consider two scenarios:

• Scenario 1: Two students take five exams. Student A consistently scores around 75%. Student B scores vary widely, from 50% to 100%. Both students have an average score of 75%, but their performance profiles are vastly different.
• Scenario 2: Two investment portfolios have the same average annual return over a 10-year period. However, one portfolio experiences significant fluctuations in returns each year, while the other provides more stable, consistent growth.

In both cases, relying solely on the average would paint an incomplete and potentially misleading picture. Measures of spread allow us to quantify the variability and understand the nuances within the data, leading to more informed decisions.

2. Key Measures for Comparing Data Spread

Several measures of spread are commonly used in statistics, each providing a different perspective on data variability. Here’s an overview of the most important ones:

2.1. Range: The Simplest Measure

The range is the simplest measure of spread to calculate. It’s simply the difference between the maximum and minimum values in a dataset.

• Formula: Range = Maximum value – Minimum value

• Example: In the student exam scenario, if Student A’s scores range from 70% to 80%, their range is 10%. If Student B’s scores range from 50% to 100%, their range is 50%.

• Advantages: Easy to understand and calculate.

• Disadvantages: Highly sensitive to outliers (extreme values). A single outlier can drastically inflate the range, misrepresenting the overall spread of the data. Only considers the two extreme values, ignoring the distribution of values in between.

2.2. Variance: Measuring Average Squared Deviation

Variance is a measure of how far individual data points are spread out from the mean (average) of the dataset. It quantifies the average squared difference between each data point and the mean.

• Formula:

  • Population Variance (σ²): σ² = Σ(x_i – μ)² / N where:
    • x_i represents each individual data point in the population
    • μ is the population mean
    • N is the total number of data points in the population
    • Σ means “sum of”
  • Sample Variance (s²): s² = Σ(x_i – x̄)² / (n-1) where:
    • x_i represents each individual data point in the sample
    • x̄ is the sample mean
    • n is the total number of data points in the sample
    • Σ means “sum of”
    • (n-1) is the degrees of freedom, used to provide an unbiased estimate of the population variance.

Explanation:

1. Calculate the mean (average) of the data set.
2. For each data point, subtract the mean and square the result (this is the squared deviation).
3. Sum up all the squared deviations.
4. Divide the sum of squared deviations by the number of data points (for population variance) or by the number of data points minus 1 (for sample variance).

• Example: Consider the following dataset: 4, 8, 6, 5, 3

  1. Mean = (4+8+6+5+3)/5 = 5.2
  2. Squared deviations: (4-5.2)² = 1.44; (8-5.2)² = 7.84; (6-5.2)² = 0.64; (5-5.2)² = 0.04; (3-5.2)² = 4.84
  3. Sum of squared deviations: 1.44 + 7.84 + 0.64 + 0.04 + 4.84 = 14.8
  4. Sample Variance: 14.8 / (5-1) = 3.7

• Advantages: Takes into account all data points in the dataset. Provides a more comprehensive measure of spread than the range.

• Disadvantages: The units are squared, making it difficult to interpret directly. Sensitive to outliers, as squaring the deviations gives more weight to extreme values.

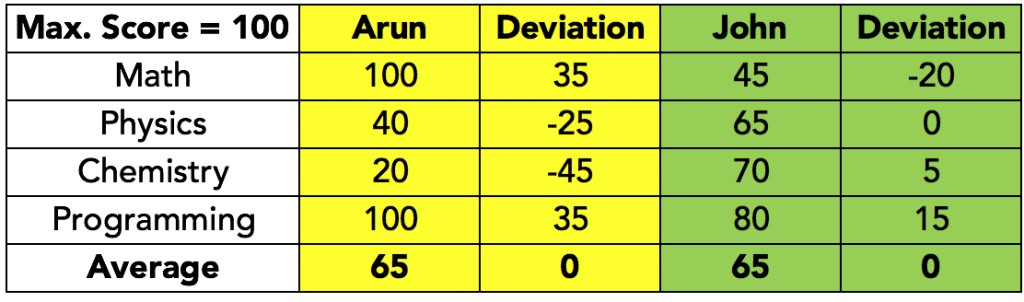
Caption: Calculation of average deviations shows how positive and negative deviations cancel each other out, resulting in a misleadingly low average.

2.3. Standard Deviation: The Square Root of Variance

Standard deviation is the most commonly used measure of spread. It is simply the square root of the variance.

• Formula:

  • Population Standard Deviation (σ): σ = √σ² = √[Σ(x_i – μ)² / N]
  • Sample Standard Deviation (s): s = √s² = √[Σ(x_i – x̄)² / (n-1)]

Explanation:

1. Calculate the variance (either population or sample variance).
2. Take the square root of the variance.

• Example: Using the same dataset as above (4, 8, 6, 5, 3), the sample variance was calculated as 3.7. Therefore, the sample standard deviation is √3.7 = 1.92 (approximately).

• Advantages: Expressed in the same units as the original data, making it easier to interpret. Provides a good balance between sensitivity to all data points and interpretability. Widely used and understood in statistical analysis.

• Disadvantages: Still somewhat sensitive to outliers, although less so than the range or variance.

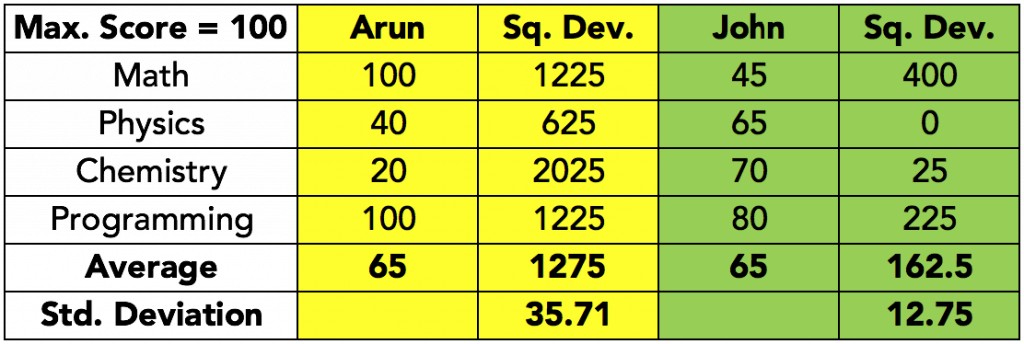
Caption: Standard deviation calculation restoring the original units to the data by taking the square root of the variance.

2.4. Interquartile Range (IQR): Focusing on the Middle 50%

The interquartile range (IQR) is a measure of spread that represents the range of the middle 50% of the data. It is calculated as the difference between the third quartile (Q3) and the first quartile (Q1).

Explanation of Quartiles:

When you divide an ordered dataset into four equal parts, you get quartiles:

• Q1 (First Quartile): The value below which 25% of the data falls.

• Q2 (Second Quartile): The median, the value below which 50% of the data falls.

• Q3 (Third Quartile): The value below which 75% of the data falls.

• Formula: IQR = Q3 – Q1

Steps to Calculate IQR:

1. Order the dataset from smallest to largest.
2. Find the median (Q2) of the dataset.
3. Find the median of the lower half of the data (excluding Q2 if N is odd). This is Q1.
4. Find the median of the upper half of the data (excluding Q2 if N is odd). This is Q3.
5. Calculate IQR = Q3 – Q1

• Example: Consider the following dataset: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20

  1. Ordered dataset: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
  2. Q2 (Median): (10+12)/2 = 11
  3. Q1 (Median of lower half): (6+8)/2 = 7
  4. Q3 (Median of upper half): (16+18)/2 = 17
  5. IQR = 17 – 7 = 10

• Advantages: Resistant to outliers. It focuses on the central portion of the data and ignores extreme values. Provides a good measure of spread for skewed distributions.

• Disadvantages: Doesn’t take into account all data points in the dataset. May not capture the full extent of variability if the tails of the distribution are important.

2.5. Mean Absolute Deviation (MAD): Average of Absolute Deviations

The Mean Absolute Deviation (MAD) is the average of the absolute differences between each data point and the mean of the dataset. This measure quantifies the average distance of data points from the center without considering the direction (positive or negative) of the deviations.

• Formula: MAD = Σ|x_i – x̄| / n

  • Where:
    • x_i represents each individual data point in the dataset
    • x̄ is the mean of the dataset
    • n is the total number of data points in the dataset
    • | | denotes absolute value (the distance from zero)
    • Σ means “sum of”

Explanation:

1. Calculate the mean (average) of the data set.
2. For each data point, subtract the mean and take the absolute value of the result (this is the absolute deviation).
3. Sum up all the absolute deviations.
4. Divide the sum of absolute deviations by the number of data points.

• Example: Consider the following dataset: 4, 8, 6, 5, 3

  1. Mean = (4+8+6+5+3)/5 = 5.2
  2. Absolute deviations: |4-5.2| = 1.2; |8-5.2| = 2.8; |6-5.2| = 0.8; |5-5.2| = 0.2; |3-5.2| = 2.2
  3. Sum of absolute deviations: 1.2 + 2.8 + 0.8 + 0.2 + 2.2 = 7.2
  4. MAD: 7.2 / 5 = 1.44

• Advantages: Easy to understand and calculate. Less sensitive to outliers compared to variance and standard deviation. Provides a straightforward measure of average deviation from the mean.

• Disadvantages: Less commonly used than standard deviation. Can be less mathematically convenient for some statistical calculations.

3. Choosing the Right Measure of Spread

The best measure of spread to use depends on the specific characteristics of the data and the goals of the analysis. Here’s a guide:

• For quick, simple comparisons: The range can be useful for a basic understanding of the data’s spread, but be mindful of its sensitivity to outliers.
• For most statistical analyses: Standard deviation is generally the preferred measure of spread due to its interpretability, widespread use, and mathematical properties.
• When outliers are present or the data is skewed: IQR is a more robust measure of spread that is less affected by extreme values.
• When a simple, intuitive measure of average deviation is needed: MAD provides a clear representation of how far data points typically deviate from the mean.

Consider this table comparing each measure:

Measure	Formula	Advantages	Disadvantages
Range	Max Value – Min Value	Simple, easy to calculate and understand.	Highly sensitive to outliers, doesn’t consider the distribution of data points.
Variance	Σ(xi – x̄)2 / (n-1)	Considers all data points, provides a comprehensive measure of spread.	Units are squared, making it hard to interpret; sensitive to outliers.
Standard Deviation	√[Σ(xi – x̄)2 / (n-1)]	Expressed in original units, easy to interpret; widely used.	Somewhat sensitive to outliers.
IQR	Q3 – Q1	Resistant to outliers, focuses on the middle 50% of the data.	Doesn’t take into account all data points, may not capture variability in the tails of the distribution.
MAD	Σ	xi – x̄	/ n

4. Practical Applications of Comparing Data Spread

Understanding and comparing data spread has numerous applications in various fields:

• Finance: Assessing the risk of investments by comparing the standard deviation of returns. A higher standard deviation indicates greater volatility and therefore higher risk.
• Manufacturing: Monitoring the consistency of production processes by tracking the range or standard deviation of product dimensions. Increased spread may signal problems with the manufacturing process.
• Education: Evaluating student performance by analyzing the spread of test scores. A smaller spread indicates more consistent performance across the class.
• Healthcare: Analyzing the variability of patient vital signs to identify potential health issues. Significant deviations from a patient’s normal range may warrant further investigation.
• Sports: Comparing the consistency of athletes by examining the standard deviation of their performance metrics. An athlete with a lower standard deviation is generally more reliable.
• Marketing: Understanding customer behavior by analyzing the spread of purchase amounts or website engagement metrics. A wider spread may indicate diverse customer segments.

5. Examples of Data Spread in Different Scenarios

Let’s explore how measures of spread can be applied in specific scenarios:

5.1. Comparing Investment Options

Imagine you are deciding between two investment options, Portfolio A and Portfolio B. Both have an average annual return of 8% over the past 10 years. However, their annual returns vary as follows:

• Portfolio A: 6%, 7%, 9%, 8%, 10%, 5%, 9%, 7%, 8%, 11%
• Portfolio B: 2%, 15%, 3%, 14%, 1%, 16%, 0%, 17%, 4%, 8%

To assess the risk associated with each portfolio, we can calculate their standard deviations:

• Portfolio A Standard Deviation: Approximately 1.87%
• Portfolio B Standard Deviation: Approximately 6.32%

Portfolio B has a significantly higher standard deviation, indicating greater volatility and therefore higher risk. While both portfolios have the same average return, Portfolio A offers a more consistent and predictable return stream. An investor who prioritizes stability might prefer Portfolio A, while an investor comfortable with higher risk might be drawn to Portfolio B’s potential for higher returns (and losses).

5.2. Evaluating Manufacturing Process Control

A manufacturing company produces bolts. The target diameter for the bolts is 10mm. To ensure quality control, the company regularly measures the diameter of a sample of bolts. Here are the measurements (in mm) for two different production runs:

• Run 1: 9.8, 10.1, 10.0, 9.9, 10.2, 9.7, 10.3, 10.0
• Run 2: 9.0, 11.0, 9.5, 10.5, 8.5, 11.5, 9.2, 10.8

Let’s calculate the range and standard deviation for each run:

• Run 1:
  • Range: 10.3 – 9.7 = 0.6 mm
  • Standard Deviation: Approximately 0.19 mm
• Run 2:
  • Range: 11.5 – 8.5 = 3.0 mm
  • Standard Deviation: Approximately 0.98 mm

Run 2 has a much larger range and standard deviation, indicating that the production process is less consistent and producing bolts with more variation in diameter. This suggests that there may be problems with the machinery or the process that need to be addressed to improve quality control.

5.3. Analyzing Student Test Scores

In a class of 30 students, two different teaching methods were used for two different units. After each unit, a test was administered. Here are the scores for the two units:

• Unit 1 (Method A): Scores ranged from 60 to 95, with most scores clustered around 75.
• Unit 2 (Method B): Scores ranged from 40 to 100, with scores more evenly distributed.

Without the actual data points, we can still infer information about the spread based on the range and distribution:

• Unit 1 (Method A): The narrower range and clustering around 75 suggest a smaller standard deviation, indicating more consistent performance.
• Unit 2 (Method B): The wider range and more even distribution suggest a larger standard deviation, indicating more variability in performance.

If the average score for both units was similar, the teacher might conclude that Method A led to more consistent learning outcomes, while Method B resulted in a wider range of understanding. Further investigation might be needed to understand why some students excelled under Method B while others struggled.

6. Data Visualization Techniques for Understanding Spread

Visualizing data can provide valuable insights into its spread and distribution. Here are some commonly used techniques:

• Histograms: Display the frequency distribution of data, showing how many values fall within specific ranges or bins. Histograms can reveal the shape of the distribution (e.g., symmetrical, skewed) and identify potential outliers.

• Box Plots: Provide a visual summary of the data’s quartiles, median, and outliers. The box represents the IQR (the middle 50% of the data), and the whiskers extend to the minimum and maximum values within a certain range (typically 1.5 times the IQR). Outliers are plotted as individual points beyond the whiskers.

• Scatter Plots: Show the relationship between two variables. By observing the spread of points on the scatter plot, you can assess the degree of correlation and identify any patterns or clusters.

• Dot Plots: Similar to histograms, but each data point is represented by a dot. Dot plots are useful for visualizing the distribution of small datasets and identifying clusters or gaps.

• Stem-and-Leaf Plots: A combination of numerical and graphical representation. They display the actual data values while also providing a visual impression of the distribution.

By using these visualization techniques, you can gain a better understanding of the spread of your data and identify potential trends or anomalies.

7. Tools for Comparing Data Spread

Several software packages and tools can help you calculate and compare measures of spread:

• Microsoft Excel: Offers built-in functions for calculating range, variance, standard deviation, and quartiles.
• Google Sheets: Similar to Excel, with functions for calculating measures of spread.
• SPSS: A statistical software package with advanced capabilities for data analysis and visualization.
• R: A programming language and environment for statistical computing and graphics.
• Python: A versatile programming language with libraries like NumPy and SciPy that provide functions for calculating measures of spread.
• Online Calculators: Numerous websites offer free online calculators for calculating measures of spread.

Choose the tool that best suits your needs and technical skills.

8. Common Mistakes to Avoid When Comparing Data Spread

• Ignoring Outliers: Failing to address outliers can significantly distort measures of spread like range, variance, and standard deviation. Always identify and consider the potential impact of outliers on your analysis.
• Using the Wrong Measure of Spread: Choosing an inappropriate measure of spread for the data can lead to misleading conclusions. Select the measure that is most appropriate for the data’s distribution and the goals of the analysis.
• Comparing Spread Across Different Datasets Without Context: When comparing the spread of two or more datasets, it’s important to consider their context and scales. A larger standard deviation might be expected in one dataset compared to another due to differences in the underlying variables.
• Misinterpreting Standard Deviation: Remember that standard deviation measures the average deviation from the mean. It doesn’t tell you anything about the shape of the distribution or the presence of outliers.
• Relying Solely on Measures of Spread: Measures of spread should be interpreted in conjunction with measures of central tendency and other descriptive statistics to provide a complete picture of the data.

9. Advanced Concepts Related to Data Spread

• Coefficient of Variation (CV): A standardized measure of spread that expresses the standard deviation as a percentage of the mean. It is useful for comparing the spread of datasets with different units or scales.
• Skewness: A measure of the asymmetry of a distribution. Positive skewness indicates a longer tail on the right side of the distribution, while negative skewness indicates a longer tail on the left side.
• Kurtosis: A measure of the “tailedness” of a distribution. High kurtosis indicates a distribution with heavy tails and more outliers, while low kurtosis indicates a distribution with lighter tails.
• Chebyshev’s Inequality: States that for any distribution, at least (1 – 1/k²) of the data will fall within k standard deviations of the mean. This inequality provides a general guideline for the spread of data, regardless of the distribution’s shape.
• Empirical Rule (68-95-99.7 Rule): For a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations, and 99.7% falls within three standard deviations.

These advanced concepts provide a deeper understanding of data spread and distribution characteristics.

10. Frequently Asked Questions (FAQ) About Comparing Data Spread

1. Why is it important to compare the spread of data?
   Comparing the spread of data helps to understand the variability and consistency within a dataset, providing a more complete picture than just looking at central tendency measures like the mean.
2. What are the key measures used to compare data spread?
   The key measures include range, variance, standard deviation, interquartile range (IQR), and mean absolute deviation (MAD).
3. How does the range help in understanding data spread?
   The range, calculated as the difference between the maximum and minimum values, provides a quick and simple measure of how spread out the data is, but it’s sensitive to outliers.
4. What is variance, and how is it calculated?
   Variance measures the average squared difference between each data point and the mean, quantifying the spread around the mean. It’s calculated by summing the squared deviations from the mean and dividing by the number of data points (or n-1 for sample variance).
5. Why is standard deviation a preferred measure of spread?
   Standard deviation, the square root of the variance, is preferred because it’s expressed in the same units as the original data, making it easier to interpret and widely used in statistical analysis.
6. How does the interquartile range (IQR) differ from other measures of spread?
   The IQR, calculated as the difference between the third and first quartiles, focuses on the middle 50% of the data, making it resistant to outliers and useful for skewed distributions.
7. What is Mean Absolute Deviation (MAD), and when is it useful?
   MAD is the average of the absolute differences between each data point and the mean, providing a straightforward measure of average deviation without considering direction. It’s less sensitive to outliers than variance or standard deviation.
8. How do outliers affect measures of data spread?
   Outliers can significantly distort measures like the range, variance, and standard deviation. The IQR and MAD are more robust against outliers, as they focus on the central portion of the data.
9. In which situations is the Coefficient of Variation (CV) useful?
   The Coefficient of Variation, which expresses the standard deviation as a percentage of the mean, is useful for comparing the spread of datasets with different units or scales.
10. What visualization techniques can help understand data spread?
    Histograms, box plots, scatter plots, dot plots, and stem-and-leaf plots are useful visualization techniques for understanding data spread.

11. COMPARE.EDU.VN: Your Partner in Data Comparison

Do you find yourself struggling to make sense of complex datasets? Are you overwhelmed by the variability and uncertainty in your data? At COMPARE.EDU.VN, we understand the challenges of comparing data and making informed decisions.

Our website offers a comprehensive suite of tools and resources to help you analyze and interpret data effectively. We provide:

• Detailed Comparisons: In-depth analyses of various data sets, highlighting key differences in spread, central tendency, and distribution.
• Easy-to-Use Calculators: Convenient online calculators for computing measures of spread like range, variance, standard deviation, and IQR.
• Visualizations: Interactive charts and graphs that allow you to explore data distributions and identify patterns.
• Expert Insights: Articles and tutorials that explain statistical concepts in a clear and accessible manner.

Whether you’re a student, researcher, business professional, or simply someone who wants to make better decisions, COMPARE.EDU.VN can empower you to unlock the insights hidden within your data.

Visit COMPARE.EDU.VN today to explore our resources and start making data-driven decisions with confidence.

Address: 333 Comparison Plaza, Choice City, CA 90210, United States
Whatsapp: +1 (626) 555-9090
Website: COMPARE.EDU.VN

Don’t let data overwhelm you. Let compare.edu.vn be your guide to data comparison and informed decision-making.