**How to Compare Stem and Leaf Diagrams Effectively**

Comparing stem and leaf diagrams can seem daunting, but COMPARE.EDU.VN makes it easy to understand data distribution and identify key statistical measures such as median, mode, and range. This guide will provide a comprehensive overview on how to compare stem plots, enhancing your ability to analyze and interpret data effectively, helping you to draw meaningful conclusions. Learn about comparative data representation today.

Comparing stem and leaf plots is crucial for data analysis, allowing for quick identification of central tendencies, spread, and distribution shape. Dive into this guide by compare.edu.vn to discover how these plots preserve numerical values while revealing data patterns, with insights into distribution shape and outliers. Enhance data literacy and decision-making skills through comparison, distribution analysis, and comparative statistics.

1. Understanding Stem and Leaf Diagrams

A stem and leaf diagram, also known as a stem plot, is a graphical method used in exploratory data analysis to visualize the shape of a distribution while retaining the original data values. It is particularly useful for small to moderately sized data sets. Before diving into How To Compare Stem And Leaf Diagrams, it’s crucial to understand their basic structure and components.

1.1. What is a Stem and Leaf Diagram?

A stem and leaf diagram is a way to represent quantitative data in a graphical format. It allows you to see the distribution of data and identify key statistical measures at a glance. This type of diagram is especially useful because it preserves the original data values, making it easier to interpret the data compared to other graphical representations like histograms.

The primary purpose of a stem and leaf diagram is to display the distribution of a univariate dataset. Unlike histograms that group data into intervals, stem plots show each individual data point in a way that reveals both the central tendency and spread of the data.

1.2. Components of a Stem and Leaf Diagram

A stem and leaf diagram consists of two main parts: the stem and the leaf.

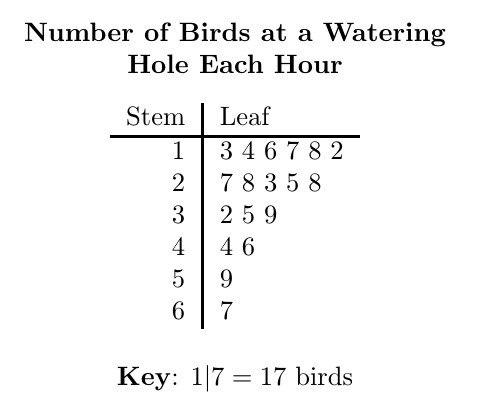
• Stem: The stem represents the leading digit(s) of the data values. It is typically the leftmost digit or digits. For example, if you have the number 32, the stem would be 3.
• Leaf: The leaf represents the trailing digit of the data values. For the number 32, the leaf would be 2.

The stem is listed in a column on the left side of the diagram, and the corresponding leaves are listed to the right, in increasing order. This arrangement provides a quick visual representation of the data distribution.

1.3. Constructing a Stem and Leaf Diagram

To construct a stem and leaf diagram, follow these steps:

1. Identify the stems: Determine the common leading digits for your data set. These will form the stems of the diagram.
2. List the stems: Write the stems in a vertical column, from smallest to largest.
3. Add the leaves: For each data value, write the trailing digit (leaf) next to its corresponding stem.
4. Order the leaves: Within each row, arrange the leaves in increasing order.
5. Add a key: Include a key that explains what the stems and leaves represent. For example, “2 | 5 means 25.”

Let’s illustrate with an example. Suppose you have the following data set: 22, 25, 28, 31, 33, 33, 36, 40, 41, 45.

1. Identify the stems: The stems are 2, 3, and 4.

2. List the stems:

   2 |
   3 |
   4 |

3. Add the leaves:

   2 | 2 5 8
   3 | 1 3 3 6
   4 | 0 1 5

4. Order the leaves: The leaves are already in order in this example.

5. Add a key: Key: 2 | 2 means 22.

1.4. Advantages and Disadvantages of Stem and Leaf Diagrams

Stem and leaf diagrams offer several advantages:

• Preserves Data: Unlike histograms, stem plots retain the original data values, allowing for more detailed analysis.
• Visual Representation: Provides a clear visual representation of the data distribution, making it easy to identify patterns and outliers.
• Simple to Construct: Relatively easy to create by hand, making it a useful tool for quick data analysis.

However, there are also some disadvantages:

• Limited to Small Data Sets: Can become unwieldy with large data sets.
• Not Suitable for Continuous Data: Best suited for discrete data or data that can be easily rounded to discrete values.
• Subjectivity: The choice of stems can sometimes be subjective, affecting the appearance of the diagram.

Understanding the basics of constructing and interpreting stem and leaf diagrams is crucial before you start comparing them. The components of a stem and leaf diagram include the stem, which represents the leading digits, and the leaf, which represents the trailing digits.

2. Key Statistical Measures

Before you can effectively compare stem and leaf diagrams, it’s essential to understand the key statistical measures that can be derived from them. These measures help you quantify and interpret the data, making it easier to draw meaningful comparisons.

2.1. Measures of Central Tendency

Measures of central tendency describe the typical or central value in a data set. The three most common measures are the mean, median, and mode.

• Mean: The mean is the average of all the data values. It is calculated by summing all the values and dividing by the number of values. While stem and leaf diagrams do not directly provide the mean, you can easily calculate it from the original data.

  Mean = (Sum of all values) / (Number of values)

• Median: The median is the middle value in a data set when the values are arranged in ascending order. In a stem and leaf diagram, the median can be easily found by locating the middle value. If there is an even number of data points, the median is the average of the two middle values.

• Mode: The mode is the value that appears most frequently in a data set. In a stem and leaf diagram, the mode is the value with the most leaves associated with a single stem.

2.2. Measures of Dispersion

Measures of dispersion describe the spread or variability of the data. Common measures include the range, interquartile range (IQR), and standard deviation.

• Range: The range is the difference between the maximum and minimum values in a data set. In a stem and leaf diagram, the range can be easily found by subtracting the smallest value (the first leaf of the smallest stem) from the largest value (the last leaf of the largest stem).

  Range = Maximum value – Minimum value

• Interquartile Range (IQR): The IQR is the range of the middle 50% of the data. It is calculated as the difference between the third quartile (Q3) and the first quartile (Q1). Quartiles divide the data into four equal parts. Q1 is the median of the lower half of the data, and Q3 is the median of the upper half.

  IQR = Q3 – Q1

• Standard Deviation: The standard deviation measures the average distance of the data values from the mean. While not directly obtainable from a stem and leaf diagram, you can calculate it from the original data.

  Standard Deviation = √[(Σ(xᵢ – μ)²)/N]

  Where:

  • xᵢ represents each individual data value.
  • μ is the mean of the data set.
  • N is the number of data values.
  • Σ means the sum of.

2.3. Identifying Outliers

Outliers are data values that are significantly different from the other values in the data set. They can be identified using the IQR. A common rule is that a value is considered an outlier if it is:

• Less than Q1 – 1.5 * IQR
• Greater than Q3 + 1.5 * IQR

In a stem and leaf diagram, outliers will appear as isolated values far from the main body of the data.

2.4. Distribution Shape

The shape of the distribution refers to the overall pattern of the data. Common distribution shapes include:

• Symmetric: The data is evenly distributed around the mean, forming a bell-shaped curve.
• Skewed Right: The data has a long tail extending to the right, indicating that there are some high values that are much larger than the rest of the data.
• Skewed Left: The data has a long tail extending to the left, indicating that there are some low values that are much smaller than the rest of the data.
• Uniform: The data is evenly distributed across all values.
• Bimodal: The data has two distinct peaks, indicating that there are two common values or clusters of values.

By examining the shape of a stem and leaf diagram, you can quickly assess the distribution of the data and identify potential skewness or bimodality.

Understanding these key statistical measures is crucial for comparing stem and leaf diagrams effectively. These measures provide a quantitative basis for comparing the central tendency, dispersion, and shape of the data distributions.

Key statistical measures such as central tendency, dispersion, outliers, and distribution shape are vital for interpreting stem and leaf diagrams. These metrics help quantify and compare data distributions.

3. Steps to Compare Stem and Leaf Diagrams

Comparing stem and leaf diagrams involves a systematic approach to identify similarities and differences between the datasets. Here are the steps to effectively compare two or more stem and leaf diagrams.

3.1. Visual Inspection

The first step in comparing stem and leaf diagrams is to visually inspect them. Look for general patterns and shapes in the data distribution.

1. Shape: Observe the overall shape of each diagram. Is it symmetric, skewed, uniform, or bimodal? Note any differences in the shapes of the distributions.
2. Spread: Assess the spread of the data. How wide is each distribution? Are the data values clustered tightly together, or are they more dispersed?
3. Gaps: Look for any gaps in the data. Are there any stems with no leaves, indicating a lack of data values in that range?
4. Outliers: Identify any potential outliers that are far from the main body of the data.

3.2. Calculate Key Statistical Measures

After the visual inspection, calculate the key statistical measures for each diagram. This will provide a quantitative basis for comparison.

1. Central Tendency: Calculate the mean, median, and mode for each data set. Compare these measures to see if the data sets have similar central values.
2. Dispersion: Calculate the range and interquartile range (IQR) for each data set. Compare these measures to see if the data sets have similar variability.
3. Outliers: Identify any outliers using the IQR method. Note the number and values of outliers in each data set.

3.3. Create Comparative Tables

To facilitate comparison, create tables that summarize the key statistical measures for each data set. This will allow you to easily see the differences and similarities between the data sets.

Here’s an example of a comparative table:

Statistic	Data Set 1	Data Set 2
Mean	50.2	52.5
Median	51	53
Mode	48	55
Range	30	35
IQR	15	17
Number of Outliers	1	2
Distribution Shape	Symmetric	Skewed

3.4. Analyze and Interpret

Once you have calculated the key statistical measures and created comparative tables, analyze and interpret the results.

1. Compare Central Tendency: Are the means, medians, and modes similar across the data sets? If so, the data sets may have similar average values.
2. Compare Dispersion: Are the ranges and IQRs similar across the data sets? If so, the data sets may have similar variability.
3. Compare Outliers: Do the data sets have similar numbers and values of outliers? Outliers can have a significant impact on the mean and standard deviation, so it’s important to consider their influence.
4. Compare Distribution Shapes: Do the data sets have similar distribution shapes? If so, the data sets may have similar underlying patterns.
5. Draw Conclusions: Based on your analysis, draw conclusions about the similarities and differences between the data sets. Are they essentially the same, or are there significant differences?

3.5. Examples of Comparative Analysis

Let’s go through some examples to illustrate how to compare stem and leaf diagrams.

Example 1: Comparing Exam Scores

Suppose you have the following stem and leaf diagrams representing the exam scores of two different classes:

Class A:

5 | 5 8
6 | 0 2 5 7
7 | 1 3 5 8
8 | 0 2 5 8
9 | 0 2

Class B:

5 | 0 2
6 | 3 5 8
7 | 0 2 5 7
8 | 1 3 6
9 | 1 3 5

1. Visual Inspection: Both diagrams appear to be roughly symmetric, but Class B seems to have a slightly higher concentration of scores in the 80s and 90s.
2. Calculate Key Statistical Measures:

Statistic	Class A	Class B
Mean	75.5	76.5
Median	75	76
Mode	80, 85, 88	63, 65, 68, 70, 72, 75, 77, 81, 83, 86, 91, 93, 95
Range	37	45
IQR	14.5	16
Number of Outliers	0	0

3. Analyze and Interpret:

   • Central Tendency: The means and medians are very similar, indicating that both classes have similar average scores.
   • Dispersion: The ranges and IQRs are also similar, indicating that both classes have similar variability in scores.
   • Distribution Shapes: Both distributions are roughly symmetric, suggesting that the scores are evenly distributed around the mean.

Conclusion: Based on this analysis, you can conclude that the exam scores of the two classes are very similar.

Example 2: Comparing Customer Wait Times

Suppose you have the following stem and leaf diagrams representing the customer wait times (in minutes) at two different stores:

Store A:

0 | 5 8
1 | 0 2 5 7
2 | 1 3 5 8
3 | 0 2

Store B:

0 | 0 2
1 | 3 5 8
2 | 0 2 5 7
3 | 1 3 5
4 | 0

1. Visual Inspection: Store B seems to have longer wait times, with some customers waiting up to 40 minutes.
2. Calculate Key Statistical Measures:

Statistic	Store A	Store B
Mean	17.3	22.1
Median	16	21
Mode	None	None
Range	27	40
IQR	11	13
Number of Outliers	0	1

3. Analyze and Interpret:

   • Central Tendency: The mean and median wait times are higher for Store B, indicating that customers generally wait longer at Store B.
   • Dispersion: The range and IQR are also higher for Store B, indicating that the wait times are more variable at Store B.
   • Outliers: Store B has one outlier (40 minutes), which could be a cause for concern.

Conclusion: Based on this analysis, you can conclude that customers generally wait longer at Store B, and the wait times are more variable. Store B also has an outlier, which could indicate a problem with customer service.

By following these steps, you can effectively compare stem and leaf diagrams and draw meaningful conclusions about the data.

Comparing stem and leaf diagrams involves visual inspection, calculating statistical measures, creating comparative tables, and analyzing results. This systematic approach helps identify similarities and differences between datasets.

4. Advanced Techniques for Comparison

While basic comparison techniques provide a solid foundation, more advanced techniques can offer deeper insights when comparing stem and leaf diagrams. These techniques include using split stems, back-to-back stem plots, and considering data transformations.

4.1. Split Stems

In some cases, the data values may be clustered too closely together, resulting in a stem and leaf diagram with very few stems and many leaves. This can make it difficult to see the distribution shape clearly. To address this issue, you can split the stems.

Splitting the stems involves dividing each stem into two or more rows, with each row representing a different range of leaf values. For example, you can split each stem into two rows: one for leaves 0-4 and another for leaves 5-9.

Here’s how to split stems:

1. Determine the number of splits: Decide how many rows you want to split each stem into. This will depend on the distribution of the data.
2. Assign leaf ranges: Assign each leaf value to its corresponding stem row. For example, if you split each stem into two rows, the first row would contain leaves 0-4, and the second row would contain leaves 5-9.
3. Rewrite the diagram: Rewrite the stem and leaf diagram with the split stems and corresponding leaves.

Example:

Suppose you have the following stem and leaf diagram:

2 | 0 1 2 3 4 5 6 7 8 9
3 | 0 1 2 3 4 5 6 7 8 9
4 | 0 1 2 3 4

This diagram is not very informative because the data is clustered too closely together. To split the stems, you can divide each stem into two rows: one for leaves 0-4 and another for leaves 5-9.

The split stem and leaf diagram would look like this:

2 | 0 1 2 3 4
2 | 5 6 7 8 9
3 | 0 1 2 3 4
3 | 5 6 7 8 9
4 | 0 1 2 3 4

Now, the distribution shape is much clearer.

4.2. Back-to-Back Stem Plots

When comparing two related data sets, a back-to-back stem plot can be a useful tool. A back-to-back stem plot has a common stem column in the middle, with the leaves for one data set extending to the left and the leaves for the other data set extending to the right.

Here’s how to create a back-to-back stem plot:

1. Identify the stems: Determine the common leading digits for both data sets.
2. List the stems: Write the stems in a vertical column in the middle of the diagram.
3. Add the leaves: For each data value in the first data set, write the trailing digit (leaf) to the left of its corresponding stem. For each data value in the second data set, write the trailing digit (leaf) to the right of its corresponding stem.
4. Order the leaves: Within each row, arrange the leaves in increasing order, moving away from the stem.
5. Add a key: Include a key that explains what the stems and leaves represent for each data set.

Example:

Suppose you want to compare the test scores of two different classes, A and B. You have the following data:

Class A: 62, 65, 68, 71, 73, 75, 78, 80, 82, 85

Class B: 60, 63, 66, 70, 72, 74, 76, 79, 81, 83

The back-to-back stem plot would look like this:

Class A | Stem | Class B
------- | ---- | -------
      8 5 |  6  | 0 3 6
    8 5 3 1 |  7  | 0 2 4 6 9
      5 2 0 |  8  | 1 3

Key: 6 | 0 means 60 for Class B, 0 | 6 means 60 for Class A.

This back-to-back stem plot allows you to easily compare the distributions of the two data sets.

4.3. Data Transformations

In some cases, the data may not be normally distributed, making it difficult to compare the stem and leaf diagrams effectively. To address this issue, you can apply data transformations.

Data transformations involve applying a mathematical function to the data values to make the distribution more symmetric or normal. Common transformations include:

• Log Transformation: Taking the logarithm of each data value. This is useful for data that is skewed to the right.
• Square Root Transformation: Taking the square root of each data value. This is also useful for data that is skewed to the right.
• Reciprocal Transformation: Taking the reciprocal of each data value. This is useful for data that is skewed to the right and contains zero values.

After applying a data transformation, you can create a new stem and leaf diagram using the transformed data. This may make it easier to compare the distributions and draw meaningful conclusions.

Example:

Suppose you have the following data set: 1, 2, 4, 8, 16.

This data is skewed to the right. To apply a log transformation, you would take the logarithm of each value:

log(1) = 0
log(2) ≈ 0.301
log(4) ≈ 0.602
log(8) ≈ 0.903
log(16) ≈ 1.204

The transformed data set is: 0, 0.301, 0.602, 0.903, 1.204.

You can then create a stem and leaf diagram using the transformed data.

By using these advanced techniques, you can gain deeper insights when comparing stem and leaf diagrams and draw more meaningful conclusions about the data.

Advanced techniques for comparing stem and leaf diagrams include using split stems, back-to-back stem plots, and considering data transformations. These methods provide deeper insights into data distributions.

5. Common Pitfalls and How to Avoid Them

When comparing stem and leaf diagrams, it’s important to be aware of common pitfalls that can lead to incorrect conclusions. Here are some common mistakes and how to avoid them.

5.1. Ignoring Sample Size

One of the most common mistakes is ignoring the sample size when comparing stem and leaf diagrams. The sample size can have a significant impact on the shape and variability of the distribution.

• Small Sample Sizes: With small sample sizes, the stem and leaf diagram may not accurately represent the underlying population distribution. The shape may be distorted by random variation, and outliers may have a disproportionate impact on the results.
• Large Sample Sizes: With large sample sizes, the stem and leaf diagram will provide a more accurate representation of the population distribution. However, even small differences between the data sets may be statistically significant.

To avoid this pitfall, always consider the sample size when comparing stem and leaf diagrams. If the sample sizes are small, be cautious about drawing strong conclusions. If the sample sizes are large, consider using statistical tests to determine whether the differences between the data sets are statistically significant.

5.2. Misinterpreting Skewness

Skewness refers to the asymmetry of the distribution. A common mistake is misinterpreting the direction or degree of skewness.

• Direction of Skewness: Skewness can be either positive (skewed to the right) or negative (skewed to the left). A positive skew means that the tail of the distribution extends to the right, indicating that there are some high values that are much larger than the rest of the data. A negative skew means that the tail of the distribution extends to the left, indicating that there are some low values that are much smaller than the rest of the data.
• Degree of Skewness: The degree of skewness refers to how asymmetric the distribution is. A highly skewed distribution will have a long tail and a concentration of data values at one end.

To avoid misinterpreting skewness, carefully examine the shape of the stem and leaf diagram. Look for the direction and length of the tail. Calculate the skewness coefficient, if possible, to quantify the degree of skewness.

5.3. Overlooking Outliers

Outliers are data values that are significantly different from the other values in the data set. Overlooking outliers can lead to incorrect conclusions about the central tendency and variability of the data.

• Impact on Central Tendency: Outliers can have a significant impact on the mean, pulling it towards the extreme values. The median is less affected by outliers.
• Impact on Variability: Outliers can increase the range and standard deviation, making the data appear more variable than it actually is.

To avoid overlooking outliers, carefully examine the stem and leaf diagram for isolated values that are far from the main body of the data. Use the IQR method to identify potential outliers. Consider removing outliers if they are due to errors or if they are not representative of the population.

5.4. Ignoring Context

Finally, a common mistake is ignoring the context of the data when comparing stem and leaf diagrams. The context can provide important information about the data and help you interpret the results correctly.

• Data Collection Methods: Consider how the data was collected. Were the data sets collected using the same methods? If not, there may be systematic differences between the data sets.
• Underlying Population: Consider the underlying population from which the data was sampled. Are the data sets from the same population? If not, there may be inherent differences between the data sets.
• External Factors: Consider any external factors that may have influenced the data. Were there any events or conditions that could have affected the data values?

To avoid ignoring context, gather as much information as possible about the data and the underlying population. Consider how the data was collected, the characteristics of the population, and any external factors that may have influenced the data.

By being aware of these common pitfalls and taking steps to avoid them, you can ensure that you are comparing stem and leaf diagrams effectively and drawing accurate conclusions.

Avoiding common pitfalls such as ignoring sample size, misinterpreting skewness, overlooking outliers, and ignoring context is crucial for accurate comparison of stem and leaf diagrams. These precautions ensure reliable conclusions.

6. Real-World Applications

Stem and leaf diagrams are a versatile tool with applications in various fields. Understanding these real-world applications can highlight the practical value of comparing stem and leaf diagrams.

6.1. Education

In education, stem and leaf diagrams can be used to analyze student performance on exams. By comparing the distributions of scores for different classes or different years, educators can identify trends and patterns in student achievement.

• Comparing Class Performance: Educators can compare the stem and leaf diagrams of exam scores for different classes to see if one class performed better than another. This can help identify effective teaching methods.
• Tracking Student Progress: Educators can track student progress over time by comparing the stem and leaf diagrams of scores on different exams. This can help identify students who are struggling and provide them with additional support.

Example:

A teacher wants to compare the performance of two classes on a math exam. The teacher creates stem and leaf diagrams for each class:

Class A:

6 | 5 8
7 | 0 2 5 7
8 | 1 3 5 8
9 | 0 2

Class B:

6 | 0 2
7 | 3 5 8
8 | 0 2 5 7
9 | 1 3 5

By comparing the stem and leaf diagrams, the teacher can see that Class B generally performed better on the exam. The teacher can then investigate why Class B performed better and use that information to improve teaching methods for both classes.

6.2. Healthcare

In healthcare, stem and leaf diagrams can be used to analyze patient data and identify trends in health outcomes.

• Analyzing Patient Demographics: Healthcare providers can use stem and leaf diagrams to analyze patient demographics, such as age and weight. This can help identify risk factors for certain diseases.
• Monitoring Treatment Effectiveness: Healthcare providers can monitor the effectiveness of treatments by comparing the stem and leaf diagrams of patient outcomes before and after treatment.

Example:

A doctor wants to monitor the effectiveness of a new drug for treating high blood pressure. The doctor creates stem and leaf diagrams of patient blood pressure readings before and after treatment:

Before Treatment:

12 | 0 2 5 7
13 | 1 3 5 8
14 | 0 2 5

After Treatment:

11 | 0 2 5
12 | 1 3 5 8
13 | 0 2

By comparing the stem and leaf diagrams, the doctor can see that the drug generally lowered patient blood pressure. The doctor can then continue to monitor patient blood pressure and adjust treatment as needed.

6.3. Business and Finance

In business and finance, stem and leaf diagrams can be used to analyze financial data and make informed investment decisions.

• Analyzing Stock Prices: Investors can use stem and leaf diagrams to analyze the distribution of stock prices and identify trends in the market.
• Monitoring Sales Performance: Businesses can monitor sales performance by comparing the stem and leaf diagrams of sales data for different products or different time periods.

Example:

An investor wants to analyze the performance of two different stocks. The investor creates stem and leaf diagrams of the daily stock prices for each stock:

Stock A:

25 | 0 2 5 7
26 | 1 3 5 8
27 | 0 2

Stock B:

24 | 0 2
25 | 3 5 8
26 | 0 2 5 7
27 | 1 3 5

By comparing the stem and leaf diagrams, the investor can see that Stock B generally has higher prices and is more variable. The investor can then use this information to make informed investment decisions.

6.4. Environmental Science

In environmental science, stem and leaf diagrams can be used to analyze environmental data and identify pollution trends.

• Analyzing Air Quality: Environmental scientists can use stem and leaf diagrams to analyze air quality data and identify sources of pollution.
• Monitoring Water Quality: Environmental scientists can monitor water quality by comparing the stem and leaf diagrams of water quality data for different locations or different time periods.

Example:

An environmental scientist wants to monitor the water quality of a river. The scientist creates stem and leaf diagrams of the levels of a certain pollutant in the river at two different locations:

Location A:

0 | 5 8
1 | 0 2 5 7
2 | 1 3 5

Location B:

1 | 3 5 8
2 | 0 2 5 7
3 | 1 3 5

By comparing the stem and leaf diagrams, the scientist can see that Location B generally has higher levels of the pollutant. The scientist can then investigate the source of the pollution at Location B and take steps to mitigate it.

These real-world applications demonstrate the versatility of stem and leaf diagrams as a tool for data analysis and decision-making.

Real-world applications of stem and leaf diagrams span education, healthcare, business, finance, and environmental science. These diagrams facilitate data analysis and informed decision-making across various fields.

7. Tools and Resources for Creating Stem and Leaf Diagrams

Creating stem and leaf diagrams can be done manually, but several tools and resources can simplify the process. These tools range from simple online calculators to advanced statistical software.

7.1. Online Calculators

Online calculators are a quick and easy way to create stem and leaf diagrams. These calculators typically require you to input your data, and they will automatically generate the diagram.

Examples of Online Calculators:

• StatCrunch: StatCrunch is a web-based statistical software that offers a variety of tools for data analysis, including the ability to create stem and leaf diagrams.
• Easy Calculation: Easy Calculation provides a simple online stem and leaf diagram calculator that is easy to use and requires no registration.

Advantages of Online Calculators:

• Ease of Use: Online calculators are typically very user-friendly and require no specialized knowledge.
• Accessibility: Online calculators can be accessed from any device with an internet connection.
• Speed: Online calculators can quickly generate stem and leaf diagrams from large data sets.

Disadvantages of Online Calculators:

• Limited Customization: Online calculators may offer limited customization options.
• Data Security: Be cautious about entering sensitive data into online calculators, as there may be security risks.
• Internet Dependence: Online calculators require an internet connection.

7.2. Spreadsheet Software (e.g., Excel)

Spreadsheet software like Microsoft Excel and Google Sheets can also be used to create stem and leaf diagrams. While they don’t have a built-in stem and leaf diagram function, you can create one manually using formulas and charts.

Steps to Create a Stem and Leaf Diagram in Excel:

1. Prepare the Data: Enter your data into a column in Excel.

2. Extract Stems and Leaves: Use formulas to extract the stems and leaves from the data. For example, if your data is in column A, you can use the following formulas:

   • Stem: =INT(A1/10) (for data values with two digits)
   • Leaf: =MOD(A1,10)

3. Create a Pivot Table: Use a pivot table to summarize the data by stem and leaf.

4. Display the Diagram: Manually format the pivot table to resemble a stem and leaf diagram.

Advantages of Spreadsheet Software:

• Customization: Spreadsheet software offers a high degree of customization.
• Data Management: Spreadsheet software allows you to easily manage and manipulate your data.
• Offline Access: Spreadsheet software can be used offline.

Disadvantages of Spreadsheet Software:

• Complexity: Creating a stem and leaf diagram in spreadsheet software can be more complex than using an online calculator.
• Manual Formatting: Manually formatting the diagram can be time-consuming.