Comparing ratios in math is a fundamental skill with wide-ranging applications, and COMPARE.EDU.VN is here to simplify the process. This comprehensive guide will explore various methods to compare ratios, providing clear examples and practical applications, ultimately helping you understand proportional relationships. Discover the easy way to compare ratios and proportional relationships now.
1. Understanding Ratios: The Foundation of Comparison
Before diving into the “How To Compare Ratios In Math”, it’s essential to grasp the core concept of a ratio. A ratio is a comparison of two quantities, indicating how much of one thing there is compared to another. It can be expressed in several ways:
- As a Fraction: a/b
- Using a Colon: a:b
- With the word “to”: a to b
In each case, ‘a’ and ‘b’ represent the quantities being compared. The order is crucial; a:b is different from b:a unless a = b. For example, if a cake recipe calls for 2 cups of flour and 1 cup of sugar, the ratio of flour to sugar is 2:1, meaning there are twice as many cups of flour as sugar.
1.1. Types of Ratios
- Part-to-Part Ratios: Compare one part of a whole to another part of the same whole. For instance, in a class of 30 students with 12 boys and 18 girls, the ratio of boys to girls is 12:18, which simplifies to 2:3.
- Part-to-Whole Ratios: Compare one part of a whole to the total whole. In the same class, the ratio of boys to the total number of students is 12:30, simplifying to 2:5.
- Rates: Compare quantities with different units. For example, if a car travels 120 miles in 2 hours, the rate is 120 miles/2 hours, which simplifies to 60 miles per hour.
Understanding these distinctions is crucial because the type of ratio affects how you interpret and compare them.
1.2. Simplifying Ratios
Simplifying ratios makes comparison easier. A ratio is in its simplest form when the numbers have no common factors other than 1. To simplify, find the greatest common factor (GCF) of both numbers and divide both parts of the ratio by the GCF.
For example, the ratio 12:18 can be simplified. The GCF of 12 and 18 is 6. Dividing both numbers by 6 gives the simplified ratio of 2:3. Simplified ratios provide a clearer understanding of the relationship between the quantities.
1.3. Equivalent Ratios
Equivalent ratios express the same relationship between quantities, even if the numbers are different. You can find equivalent ratios by multiplying or dividing both parts of the ratio by the same non-zero number.
For example, 2:3, 4:6, and 6:9 are equivalent ratios because they all express the same relationship. Multiplying 2:3 by 2 gives 4:6, and multiplying by 3 gives 6:9. Understanding equivalent ratios is fundamental when comparing ratios, as it allows you to put them in a comparable form.
2. Why Compare Ratios? Real-World Applications
Comparing ratios isn’t just an abstract mathematical exercise; it’s a practical skill used in numerous real-world scenarios. Here are some compelling examples:
- Cooking and Baking: Recipes often use ratios to maintain consistency in flavor and texture. For example, a baker might need to scale a recipe up or down while preserving the ratio of ingredients.
- Business and Finance: Businesses use ratios to analyze financial performance, compare profitability, and assess risk. Financial ratios like debt-to-equity ratio or current ratio help stakeholders make informed decisions.
- Science and Engineering: Scientists and engineers use ratios in various calculations, such as determining the concentration of solutions, scaling models, or analyzing data.
- Healthcare: In medicine, ratios are used to calculate drug dosages, interpret lab results, and monitor patient health. For example, the ratio of red blood cells to plasma is a critical indicator of dehydration.
- Sports and Gaming: Ratios are used to calculate win-loss records, determine player statistics, and design game mechanics.
The ability to compare ratios effectively allows for informed decision-making and problem-solving across diverse fields.
2.1. Identifying Proportional Relationships
Comparing ratios is fundamental to identifying proportional relationships. Two ratios are proportional if they are equivalent. This means that the relationship between the quantities is consistent.
For example, if 2 apples cost $1 and 4 apples cost $2, the ratios 2:1 and 4:2 are proportional because they both simplify to 2:1. Proportional relationships are common in everyday situations, such as calculating the cost of multiple items, converting units, or scaling recipes.
2.2. Solving Proportions
A proportion is an equation stating that two ratios are equal. Solving proportions is a common application of ratio comparison. To solve a proportion, you can use cross-multiplication or other algebraic methods.
For example, if a recipe calls for 2 cups of flour for every 3 eggs, and you want to make a larger batch using 9 eggs, you can set up the proportion 2/3 = x/9. Cross-multiplying gives 3x = 18, so x = 6. You would need 6 cups of flour.
2.3. Comparing Scales and Models
Ratios are essential when working with scales and models. A scale is a ratio that compares the size of a model to the size of the actual object.
For example, if a map has a scale of 1:100000, it means that 1 unit on the map represents 100000 units in reality. Comparing ratios allows you to convert measurements between the model and the real object accurately.
3. Methods for Comparing Ratios: A Step-by-Step Guide
Several methods can be used to compare ratios effectively. Here are some of the most common and straightforward techniques:
3.1. Simplifying to a Common Denominator
One of the most intuitive methods to compare ratios is to express them as fractions and find a common denominator. This allows you to directly compare the numerators.
- Step 1: Express Ratios as Fractions: Write each ratio as a fraction. For example, if you want to compare 3:4 and 5:6, write them as 3/4 and 5/6.
- Step 2: Find the Least Common Denominator (LCD): Determine the LCD of the denominators. In this case, the LCD of 4 and 6 is 12.
- Step 3: Convert Fractions to Equivalent Fractions with the LCD: Convert each fraction to an equivalent fraction with the LCD as the denominator.
- 3/4 = (3 3) / (4 3) = 9/12
- 5/6 = (5 2) / (6 2) = 10/12
- Step 4: Compare Numerators: Compare the numerators of the fractions. Since 10/12 > 9/12, the ratio 5:6 is greater than 3:4.
3.2. Converting to Decimals or Percentages
Another effective method is to convert ratios to decimals or percentages. This allows you to compare them directly using familiar numerical representations.
- Step 1: Express Ratios as Fractions: Write each ratio as a fraction.
- Step 2: Divide to Convert to Decimal: Divide the numerator by the denominator to convert the fraction to a decimal.
- 3/4 = 0.75
- 5/6 ≈ 0.833
- Step 3: Convert Decimal to Percentage (Optional): Multiply the decimal by 100 to convert it to a percentage.
- 0.75 = 75%
- 0.833 ≈ 83.3%
- Step 4: Compare Decimals or Percentages: Compare the decimals or percentages. Since 0.833 > 0.75, the ratio 5:6 is greater than 3:4.
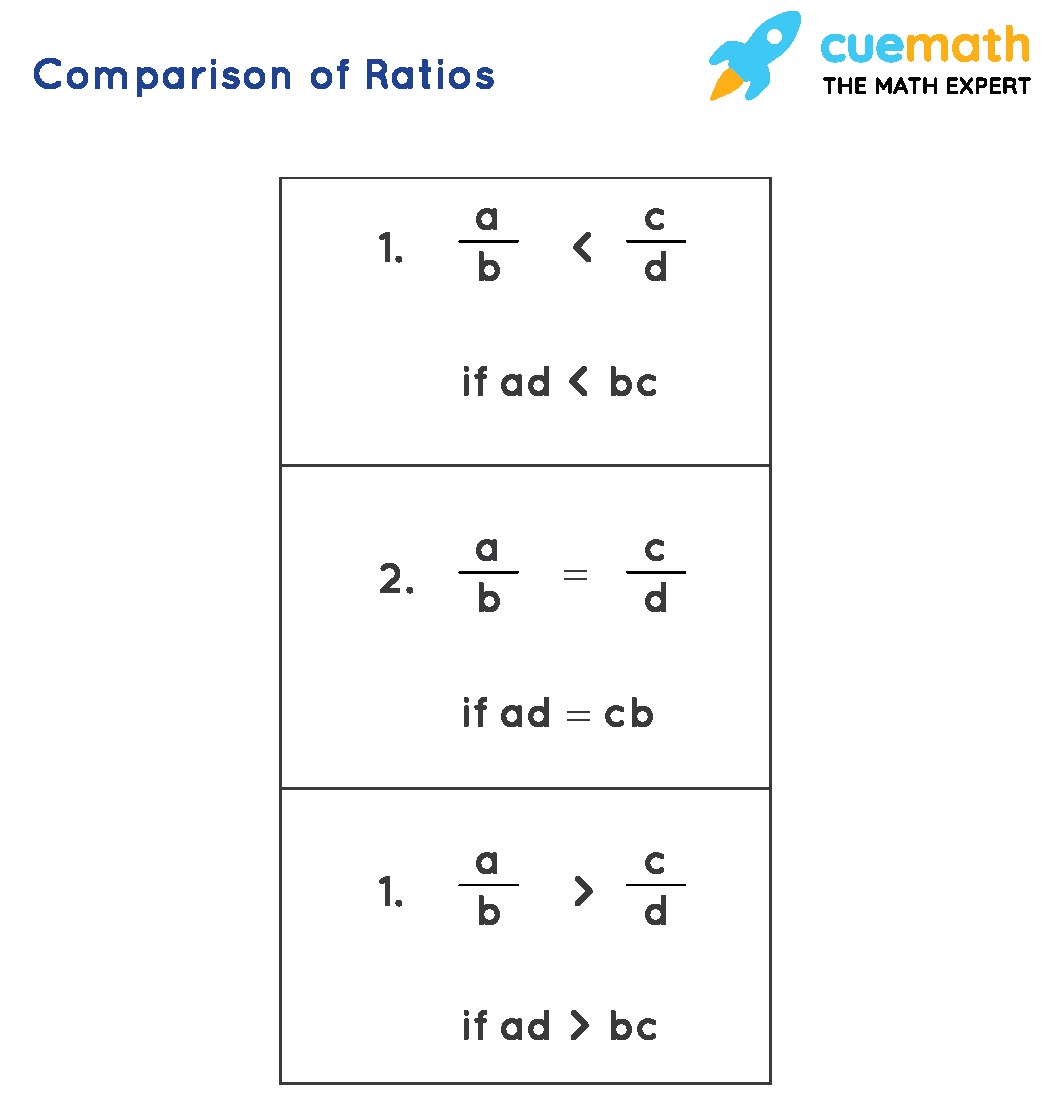
3.3. Cross-Multiplication Method
Cross-multiplication is a quick and efficient method to compare two ratios without finding a common denominator.
- Step 1: Write Ratios as Fractions: Write each ratio as a fraction.
- Step 2: Cross-Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and the numerator of the second fraction by the denominator of the first fraction.
- For 3/4 and 5/6:
- 3 * 6 = 18
- 5 * 4 = 20
- For 3/4 and 5/6:
- Step 3: Compare the Products: Compare the products of the cross-multiplication.
- If the first product is greater, the first ratio is greater.
- If the second product is greater, the second ratio is greater.
- If the products are equal, the ratios are equal.
- Since 20 > 18, the ratio 5:6 is greater than 3:4.
3.4. Using a Common Antecedent or Consequent
Sometimes, it’s helpful to manipulate the ratios so they have a common antecedent (the first number in the ratio) or a common consequent (the second number). This makes the comparison straightforward.
- Step 1: Choose a Common Antecedent or Consequent: Decide whether to make the antecedents or consequents the same.
- Step 2: Multiply Ratios to Achieve Common Value: Multiply both parts of each ratio by a factor that makes the chosen value (antecedent or consequent) the same for all ratios.
- Step 3: Compare the Remaining Values: Compare the remaining values to determine the relationship between the ratios.
For example, to compare 2:3 and 4:5 by making the antecedents the same:
- Multiply 2:3 by 2 to get 4:6.
- Now, compare 4:6 and 4:5. Since the antecedents are the same, compare the consequents.
- Since 6 > 5, the ratio 4:5 is greater than 4:6, meaning 4:5 is greater than 2:3.
4. Common Pitfalls and How to Avoid Them
While comparing ratios may seem straightforward, several common pitfalls can lead to errors. Here’s how to avoid them:
4.1. Misinterpreting the Order of Ratios
The order of quantities in a ratio is crucial. Reversing the order changes the meaning of the ratio. Always ensure you understand what each quantity represents.
- Example: The ratio of apples to oranges is 3:2. This is different from the ratio of oranges to apples, which is 2:3. Always double-check the question and the context to ensure you have the quantities in the correct order.
4.2. Not Simplifying Ratios
Comparing ratios in their simplest form makes the process easier and reduces the chance of errors. Always simplify ratios before comparing them.
- Example: Comparing 12:16 and 9:12 is easier if you simplify them first to 3:4 and 3:4, respectively. In this simplified form, it’s clear that the ratios are equal.
4.3. Incorrectly Applying Cross-Multiplication
Cross-multiplication is a powerful tool, but it must be applied correctly. Ensure you multiply the correct terms and interpret the results accurately.
- Example: When comparing a/b and c/d, you should multiply ad and bc. If ad > bc, then a/b > c/d. Make sure you don’t mix up the terms during multiplication.
4.4. Ignoring Units
When comparing ratios involving different units, make sure to convert them to the same unit before comparing. Ignoring units can lead to incorrect comparisons.
- Example: If you’re comparing 2 meters to 50 centimeters, first convert both to the same unit (e.g., 200 cm to 50 cm) before forming the ratio.
4.5. Assuming Proportionality without Verification
Just because two scenarios involve ratios doesn’t mean they are proportional. Always verify whether the ratios are equivalent before assuming proportionality.
- Example: If 2 workers can complete a task in 6 hours, it doesn’t necessarily mean that 4 workers can complete the same task in 3 hours. The relationship might not be directly proportional due to other factors.
5. Advanced Techniques and Applications
Beyond the basic methods, several advanced techniques and applications can further enhance your ability to compare ratios effectively.
5.1. Working with Three or More Ratios
When comparing three or more ratios, the same principles apply, but the process can be more complex. The goal is still to find a common basis for comparison.
- Method: Convert all ratios to fractions with a common denominator. This allows you to compare all the numerators directly.
- Example: Compare 1:2, 2:3, and 3:4. Convert them to fractions 1/2, 2/3, and 3/4. The LCD of 2, 3, and 4 is 12.
- 1/2 = 6/12
- 2/3 = 8/12
- 3/4 = 9/12
- Now, you can easily compare the ratios: 1:2 < 2:3 < 3:4.
5.2. Using Ratios in Scale Drawings and Models
Scale drawings and models use ratios to represent real-world objects accurately. Understanding how to manipulate and compare these ratios is essential for accurate interpretations.
- Method: Use the scale ratio to convert measurements from the drawing or model to the actual object, or vice versa.
- Example: A map has a scale of 1:50000. If two cities are 4 cm apart on the map, the actual distance between them is 4 cm * 50000 = 200000 cm = 2 kilometers.
5.3. Applying Ratios to Financial Analysis
Financial ratios provide insights into a company’s performance and financial health. Comparing these ratios over time or with industry benchmarks is crucial for making informed investment decisions.
- Common Ratios:
- Debt-to-Equity Ratio: Total Debt / Total Equity
- Current Ratio: Current Assets / Current Liabilities
- Profit Margin: Net Income / Revenue
- Analysis: Compare these ratios to previous periods or to industry averages to identify trends and assess the company’s financial health.
6. Practical Examples and Case Studies
To further illustrate the concepts, let’s explore some practical examples and case studies:
6.1. Case Study: Comparing Fuel Efficiency of Cars
Suppose you’re comparing the fuel efficiency of two cars:
- Car A: Travels 350 miles on 10 gallons of gas.
- Car B: Travels 420 miles on 12 gallons of gas.
To compare their fuel efficiency, calculate the miles per gallon (MPG) for each car:
- Car A: 350 miles / 10 gallons = 35 MPG
- Car B: 420 miles / 12 gallons = 35 MPG
In this case, both cars have the same fuel efficiency.
6.2. Example: Adjusting a Recipe
A recipe calls for a ratio of 2 cups of flour to 1 cup of sugar. If you want to use 3 cups of sugar, how much flour do you need?
- Set up a proportion: 2/1 = x/3
- Cross-multiply: 1 x = 2 3
- Solve for x: x = 6
You need 6 cups of flour.
6.3. Practical Application: Comparing Investment Options
You’re considering two investment options:
- Option A: Returns $500 on a $10000 investment.
- Option B: Returns $750 on a $15000 investment.
To compare the return on investment (ROI):
- Option A: ($500 / $10000) * 100% = 5%
- Option B: ($750 / $15000) * 100% = 5%
Both options have the same ROI, so other factors might influence your decision.
7. How COMPARE.EDU.VN Can Help
Navigating the complexities of comparing ratios can be simplified with the right resources. COMPARE.EDU.VN offers a comprehensive platform to assist you in various comparative tasks.
7.1. Access to Detailed Comparisons
COMPARE.EDU.VN provides detailed comparisons across various domains. Whether you’re comparing products, services, or concepts, our platform offers structured and objective analyses to aid your decision-making process.
7.2. User-Friendly Interface
The website features an intuitive interface, making it easy to find the information you need. With clear navigation and search functionalities, users can quickly access relevant comparisons and insights.
7.3. Real-Time Data and Expert Insights
COMPARE.EDU.VN ensures that the information available is up-to-date and accurate. Real-time data and expert insights are integrated to provide users with the most current and reliable comparisons.
7.4. Customized Comparison Tools
Users can customize their comparisons based on specific criteria. This feature allows you to focus on the attributes that matter most to you, ensuring that the comparison aligns with your unique needs.
7.5. Comprehensive Guides and Tutorials
To support your understanding, COMPARE.EDU.VN offers comprehensive guides and tutorials. These resources provide step-by-step instructions and explanations, enhancing your ability to make informed decisions.
COMPARE.EDU.VN is your go-to resource for objective and detailed comparisons. Make your decisions with confidence, armed with the insights you need.
8. Conclusion: Mastering Ratio Comparison
Mastering “how to compare ratios in math” is a valuable skill that extends beyond the classroom. By understanding the different methods and avoiding common pitfalls, you can confidently apply these techniques to solve real-world problems and make informed decisions. Whether you’re adjusting a recipe, analyzing financial data, or comparing fuel efficiency, the ability to compare ratios effectively will serve you well.
Remember to focus on simplifying ratios, using common denominators or cross-multiplication, and always double-checking the order and units of the quantities. With practice and the right resources, you can become proficient in comparing ratios and unlocking the power of proportional relationships.
Ready to take your comparison skills to the next level? Visit COMPARE.EDU.VN today and explore our extensive collection of comparison guides and tools. Make informed decisions with confidence, knowing you have the best information at your fingertips.
9. Frequently Asked Questions (FAQs)
9.1. What is a Ratio?
A ratio is a comparison of two quantities, indicating how much of one thing there is compared to another. It can be expressed as a fraction, using a colon, or with the word “to.”
9.2. How Do You Simplify a Ratio?
To simplify a ratio, find the greatest common factor (GCF) of both numbers and divide both parts of the ratio by the GCF. This reduces the ratio to its simplest form.
9.3. What is Cross-Multiplication and How Do You Use It?
Cross-multiplication is a method to compare two ratios written as fractions. Multiply the numerator of the first fraction by the denominator of the second fraction, and the numerator of the second fraction by the denominator of the first fraction. Compare the products to determine which ratio is greater.
9.4. How Do You Compare Three or More Ratios?
To compare three or more ratios, convert them to fractions with a common denominator. This allows you to compare the numerators directly.
9.5. Why is the Order of Quantities Important in a Ratio?
The order of quantities in a ratio is crucial because it changes the meaning of the ratio. For example, the ratio of apples to oranges is different from the ratio of oranges to apples.
9.6. What Are Some Real-World Applications of Comparing Ratios?
Real-world applications of comparing ratios include cooking and baking, business and finance, science and engineering, healthcare, and sports and gaming.
9.7. How Can COMPARE.EDU.VN Help with Comparisons?
COMPARE.EDU.VN provides detailed comparisons across various domains, offers a user-friendly interface, ensures access to real-time data and expert insights, allows customized comparisons, and provides comprehensive guides and tutorials.
9.8. What Should I Do if I Encounter Different Units While Comparing Ratios?
Convert all quantities to the same unit before comparing ratios. Ignoring units can lead to incorrect comparisons.
9.9. How Do You Identify Proportional Relationships?
Two ratios are proportional if they are equivalent. You can verify this by simplifying the ratios or using cross-multiplication.
9.10. Can Ratios Be Used in Financial Analysis?
Yes, financial ratios provide insights into a company’s performance and financial health. Comparing these ratios over time or with industry benchmarks is crucial for making informed investment decisions.
For further assistance and detailed comparisons, visit compare.edu.vn at 333 Comparison Plaza, Choice City, CA 90210, United States, or contact us via Whatsapp at +1 (626) 555-9090. We are here to help you make the best decisions with confidence.