Comparing proportions is a crucial statistical task. How To Compare Proportions effectively? COMPARE.EDU.VN offers a comprehensive guide to understanding proportions, significance level, confidence intervals and hypothesis testing, along with practical examples for data analysis. This article dives deep into comparing population proportions, covering essential elements like hypothesis testing, confidence intervals, and practical examples, offering a robust understanding of comparative analysis, comparative statistics and decision making using proportions.
1. Understanding the Basics of Comparing Proportions
Comparing proportions involves determining whether the difference between two or more proportions is statistically significant. This concept is widely used in various fields, from healthcare to marketing, to draw meaningful conclusions from data.
1.1. What are Proportions?
A proportion is a fraction or ratio indicating the part of a whole represented by a specific attribute. It is calculated by dividing the number of occurrences of an event by the total number of observations. For example, if 50 out of 200 customers prefer product A, the proportion is 50/200 = 0.25 or 25%.
1.2. Why Compare Proportions?
Comparing proportions helps in:
- Identifying Differences: Determining if observed differences are real or due to chance.
- Making Informed Decisions: Supporting decisions based on data-driven insights.
- Validating Hypotheses: Testing assumptions about populations.
- Optimizing Strategies: Refining approaches based on comparative outcomes.
1.3. Key Assumptions for Comparing Proportions
When comparing two independent population proportions, several assumptions must hold true to ensure the validity of the results:
- Independent Random Samples: The data should come from two independent simple random samples. Independence means that the selection of one sample does not affect the selection of the other.
- Sufficient Successes and Failures: Each sample must have at least five successes (observations with the attribute of interest) and five failures (observations without the attribute of interest).
- Sample Size Relative to Population Size: The population size should be at least ten to twenty times larger than the sample size. This prevents over-sampling, which can skew results.
These conditions ensure the sampling distribution of the difference in proportions is approximately normal, allowing for accurate hypothesis testing and confidence interval estimation.
2. Hypothesis Testing for Comparing Proportions
Hypothesis testing assesses whether observed differences in sample proportions provide enough evidence to reject the null hypothesis, which typically states that the population proportions are equal.
2.1. Formulating Hypotheses
The first step is to define the null and alternative hypotheses:
- Null Hypothesis (H0): States that there is no difference between the population proportions ((p_A = p_B)).
- Alternative Hypothesis (Ha): States that there is a difference between the population proportions. This can be two-tailed ((p_A neq p_B)), left-tailed ((p_A < p_B)), or right-tailed ((p_A > p_B)), depending on the research question.
2.2. Calculating the Pooled Proportion
Since the null hypothesis assumes equal proportions, we use a pooled proportion ((p_c)) to estimate the common population proportion:
[p_{c} = dfrac{x_{A} + x_{B}}{n_{A} + n_{B}}]
Where:
- (x_A) and (x_B) are the number of successes in samples A and B, respectively.
- (n_A) and (n_B) are the sample sizes of samples A and B, respectively.
2.3. Determining the Test Statistic
The test statistic (z-score) measures how many standard errors the observed difference is from the null hypothesis:
[z = dfrac{( hat{p}_{A} – hat{p}_{B}) – (p_{A} – p_{B})}{sqrt{p_{c}(1 – p_{c})left(dfrac{1}{n_{A}} + dfrac{1}{n_{B}}right)}}]
Where:
- (hat{p}_{A}) and (hat{p}_{B}) are the sample proportions.
- (p_A – p_B) is the hypothesized difference (usually 0 under the null hypothesis).
2.4. Finding the P-value
The p-value is the probability of observing a test statistic as extreme as, or more extreme than, the one calculated if the null hypothesis is true. A small p-value suggests strong evidence against the null hypothesis.
2.5. Making a Decision
Compare the p-value to the significance level ((alpha)). If the p-value is less than (alpha), reject the null hypothesis. This indicates a statistically significant difference in proportions. If the p-value is greater than (alpha), do not reject the null hypothesis.
3. Confidence Intervals for Comparing Proportions
Confidence intervals provide a range within which the true difference in population proportions is likely to fall. They are useful for estimating the magnitude of the difference.
3.1. Formula for Confidence Interval
The confidence interval for the difference between two independent population proportions is:
[hat{p}_A – hat{p}_B pm z_{frac{alpha}{2}}sqrt{frac{hat{p}_A(1-hat{p}_A)}{n_A}+frac{hat{p}_B(1-hat{p}_B)}{n_B}}]
Where:
- (hat{p}_A) and (hat{p}_B) are the sample proportions.
- (z_{frac{alpha}{2}}) is the critical value from the standard normal distribution corresponding to the desired confidence level.
- (n_A) and (n_B) are the sample sizes.
3.2. Interpreting the Confidence Interval
If the confidence interval contains zero, it suggests no significant difference between the population proportions at the given confidence level. If the interval does not contain zero, it suggests a significant difference. The sign of the interval indicates the direction of the difference (positive or negative).
4. Practical Examples of Comparing Proportions
Let’s explore some practical examples to illustrate the concepts.
4.1. Example 1: Medication Effectiveness
Two types of medication for hives are tested to determine if there is a difference in the proportions of adult patient reactions. Twenty out of a random sample of 200 adults given medication A still had hives 30 minutes after taking the medication. Twelve out of another random sample of 200 adults given medication B still had hives 30 minutes after taking the medication. Test at a 1% level of significance.
-
Step 1: Define Hypotheses
- (H_{0}: p_{A} = p_{B}) (There is no difference in proportions)
- (H_{a}: p_{A} neq p_{B}) (There is a difference in proportions)
-
Step 2: Calculate Sample Proportions
- (hat{p}_{A} = dfrac{20}{200} = 0.1)
- (hat{p}_{B} = dfrac{12}{200} = 0.06)
-
Step 3: Calculate Pooled Proportion
- [p_{c} = dfrac{20 + 12}{200 + 200} = dfrac{32}{400} = 0.08]
-
Step 4: Calculate Test Statistic
- [z = dfrac{(0.1 – 0.06) – 0}{sqrt{0.08(1 – 0.08)left(dfrac{1}{200} + dfrac{1}{200}right)}} = dfrac{0.04}{sqrt{0.0736 cdot dfrac{2}{200}}} = dfrac{0.04}{sqrt{0.000736}} approx 1.47]
-
Step 5: Calculate P-value
- For a two-tailed test, (ptext{-value} = 2 cdot P(Z > 1.47) = 2 cdot (1 – P(Z < 1.47)) = 2 cdot (1 – 0.9292) = 2 cdot 0.0708 = 0.1416)
-
Step 6: Make a Decision
- Since (alpha = 0.01) and (ptext{-value} = 0.1416), (alpha < ptext{-value}).
- Do not reject the null hypothesis.
-
Conclusion: At a 1% level of significance, there is not sufficient evidence to conclude that there is a difference in the proportions of adult patients who did not react after 30 minutes to medication A and medication B.
4.2. Example 2: Valve Pressure Tolerance
Two types of valves are tested to determine if there is a difference in pressure tolerances. Fifteen out of a random sample of 100 of Valve A cracked under 4,500 psi. Six out of a random sample of 100 of Valve B cracked under 4,500 psi. Test at a 5% level of significance.
-
Step 1: Define Hypotheses
- (H_{0}: p_{A} = p_{B})
- (H_{a}: p_{A} neq p_{B})
-
Step 2: Calculate Sample Proportions
- (hat{p}_{A} = dfrac{15}{100} = 0.15)
- (hat{p}_{B} = dfrac{6}{100} = 0.06)
-
Step 3: Calculate Pooled Proportion
- [p_{c} = dfrac{15 + 6}{100 + 100} = dfrac{21}{200} = 0.105]
-
Step 4: Calculate Test Statistic
- [z = dfrac{(0.15 – 0.06) – 0}{sqrt{0.105(1 – 0.105)left(dfrac{1}{100} + dfrac{1}{100}right)}} = dfrac{0.09}{sqrt{0.0940 cdot dfrac{2}{100}}} = dfrac{0.09}{sqrt{0.00188}} approx 2.07]
-
Step 5: Calculate P-value
- For a two-tailed test, (ptext{-value} = 2 cdot P(Z > 2.07) = 2 cdot (1 – P(Z < 2.07)) = 2 cdot (1 – 0.9808) = 2 cdot 0.0192 = 0.0384)
-
Step 6: Make a Decision
- Since (alpha = 0.05) and (ptext{-value} = 0.0384), (alpha > ptext{-value}).
- Reject the null hypothesis.
-
Conclusion: At the 5% significance level, the data support that there is a difference in the pressure tolerances between the two valves.
4.3. Example 3: Sexting Among Students
A researcher investigates gender differences in “sexting.” They hypothesize that the proportion of girls involved in “sexting” is less than the proportion of boys. Data collected in 2010 from middle and high school students shows that 156 out of 2169 girls and 183 out of 2231 boys reported sending “sexts.” Test at a 1% level of significance.
| Males | Females | |
|---|---|---|
| Sent “sexts” | 183 | 156 |
| Total number surveyed | 2231 | 2169 |
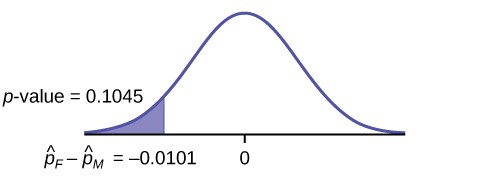


-
Step 1: Define Hypotheses
- (H_{0}: p_{F} = p_{M}) or (H_{0}: p_{F} – p_{M} = 0)
- (H_{a}: p_{F} < p_{M}) or (H_{a}: p_{F} – p_{M} < 0)
-
Step 2: Calculate Sample Proportions
- (hat{p}_{F} = dfrac{156}{2169} approx 0.0719)
- (hat{p}_{M} = dfrac{183}{2231} approx 0.0820)
-
Step 3: Calculate Pooled Proportion
- [p_{C} = dfrac{156 + 183}{2169 + 2231} = dfrac{339}{4400} approx 0.077]
-
Step 4: Calculate Test Statistic
- [z = dfrac{(0.0719 – 0.0820) – 0}{sqrt{(0.077)(0.923)left(dfrac{1}{2169} + dfrac{1}{2231}right)}} approx -1.256]
-
Step 5: Calculate P-value
- For a left-tailed test, (ptext{-value} = P(Z < -1.256) approx 0.1045)
-
Step 6: Make a Decision
- Since (alpha = 0.01) and (ptext{-value} = 0.1045), (alpha < ptext{-value}).
- Do not reject the null hypothesis.
-
Conclusion: At the 1% level of significance, there is not sufficient evidence to conclude that the proportion of girls sending “sexts” is less than the proportion of boys sending “sexts.”
4.4. Example 4: Smartphone Use Among Adults
A cell phone company claims that iPhone smartphones are more popular with whites (non-Hispanic) than with African Americans. A survey shows that 5% of 232 African American cell phone owners have an iPhone, while 10% of 1,343 white cell phone owners own an iPhone. Test at the 5% level of significance to see if the proportion of white iPhone owners is greater than the proportion of African American iPhone owners.
-
Step 1: Define Hypotheses
- (H_{0}: p_{W} = p_{A}) or (H_{0}: p_{W} – p_{A} = 0)
- (H_{a}: p_{W} > p_{A}) or ( H_{a}: p_{W} – p_{A} > 0)
-
Step 2: Calculate Sample Proportions
- (hat{p}_{W} = 0.10)
- (hat{p}_{A} = 0.05)
-
Step 3: Calculate Pooled Proportion
- First, find the number of iPhone owners in each group:
- Whites: (0.10 cdot 1343 = 134.3 approx 134)
- African Americans: (0.05 cdot 232 = 11.6 approx 12)
- [p_{C} = dfrac{134 + 12}{1343 + 232} = dfrac{146}{1575} approx 0.0927]
- First, find the number of iPhone owners in each group:
-
Step 4: Calculate Test Statistic
- [z = dfrac{(0.10 – 0.05) – 0}{sqrt{(0.0927)(0.9073)left(dfrac{1}{1343} + dfrac{1}{232}right)}} approx 2.33]
-
Step 5: Calculate P-value
- For a right-tailed test, (ptext{-value} = P(Z > 2.33) approx 0.0099)
-
Step 6: Make a Decision
- Since (alpha = 0.05) and (ptext{-value} = 0.0099), (alpha > ptext{-value}).
- Reject the (H_{0}).
-
Conclusion: At the 5% level of significance, there is sufficient evidence to conclude that a larger proportion of white cell phone owners use iPhones than African Americans.
4.5. Example 5: Forcible Rapes in Texas
A group wants to know if the proportion of forcible rapes in Texas differed between 2010 and 2011. In 2010, out of 113,231 violent crimes, 7,622 were forcible rapes. In 2011, out of 104,873 violent crimes, 7,439 were forcible rapes. Test at a 5% significance level.
-
Step 1: Define Hypotheses
- (H_{0}: p_{1} = p_{2}) or ( H_{0}: p_{1} − p_{2} = 0)
- (H_{a}: p_{1} neq p_{2}) or ( H_{a}: p_{1} − p_{2} neq 0)
-
Step 2: Calculate Sample Proportions
- (hat{p}_{1} = dfrac{7622}{113231} approx 0.0673)
- (hat{p}_{2} = dfrac{7439}{104873} approx 0.0709)
-
Step 3: Calculate Pooled Proportion
- [p_{C} = dfrac{7622 + 7439}{113231 + 104873} = dfrac{15061}{218104} approx 0.0691]
-
Step 4: Calculate Test Statistic
- [z = dfrac{(0.0673 – 0.0709) – 0}{sqrt{(0.0691)(0.9309)left(dfrac{1}{113231} + dfrac{1}{104873}right)}} approx -3.35]
-
Step 5: Calculate P-value
- For a two-tailed test, (ptext{-value} = 2 cdot P(Z < -3.35) approx 0.0008)
-
Step 6: Make a Decision
- Since (alpha = 0.05) and (ptext{-value} = 0.0008), (alpha > ptext{-value}).
-
Conclusion: At the 5% significance level, there is sufficient evidence to conclude that there is a difference between the proportion of forcible rapes in 2011 and 2010.
5. Confidence Intervals for the Difference Between Two Independent Population Proportions
Confidence intervals estimate how much larger one population proportion is than another. The interval’s center is the difference between the sample proportions, and the margin of error is the product of the z-score and the standard error.
5.1. Formula Review
The confidence interval is calculated as:
(hat{p}_A – hat{p}_B pm z_{frac{alpha}{2}}sqrt{frac{hat{p}_A(1-hat{p}_A)}{n_A}+frac{hat{p}_B(1-hat{p}_B)}{n_B}})
5.2. Practical Example 6: Puppy Adoption Rates
How much more likely are puppies to be adopted in their first week compared to older dogs? In a sample, 278 of 321 puppies were adopted in the first week, while 472 of 649 older dogs were adopted in the same period. Calculate a 95% confidence interval for the difference.
-
Step 1: Identify the Sample Proportions
- Proportion of puppies adopted: (hat{p}_{puppies} = frac{278}{321} approx 0.866)
- Proportion of older dogs adopted: (hat{p}_{dogs} = frac{472}{649} approx 0.727)
-
Step 2: Calculate the Difference in Sample Proportions
- (hat{p}_{puppies} – hat{p}_{dogs} = 0.866 – 0.727 = 0.139)
-
Step 3: Find the Critical Value
- For a 95% confidence level, (alpha = 0.05), so (frac{alpha}{2} = 0.025). The z-score for 0.025 in the tail is (z = 1.96).
-
Step 4: Calculate the Standard Error
- Standard Error = (sqrt{frac{hat{p}_{puppies}(1-hat{p}_{puppies})}{n_{puppies}} + frac{hat{p}_{dogs}(1-hat{p}_{dogs})}{n_{dogs}}})
- Standard Error = (sqrt{frac{0.866(1-0.866)}{321} + frac{0.727(1-0.727)}{649}})
- Standard Error = (sqrt{frac{0.866(0.134)}{321} + frac{0.727(0.273)}{649}})
- Standard Error = (sqrt{frac{0.116}{321} + frac{0.199}{649}})
- Standard Error = (sqrt{0.00036 + 0.00031})
- Standard Error = (sqrt{0.00067})
- Standard Error ≈ 0.0259
-
Step 5: Calculate the Margin of Error
- Margin of Error = (z cdot) Standard Error
- Margin of Error = (1.96 cdot 0.0259)
- Margin of Error ≈ 0.0508
-
Step 6: Calculate the Confidence Interval
- Confidence Interval = (Difference in Sample Proportions) ± Margin of Error
- Confidence Interval = (0.139 pm 0.0508)
- Lower bound: (0.139 – 0.0508 = 0.0882)
- Upper bound: (0.139 + 0.0508 = 0.1898)
-
Result
- With 95% confidence, puppies are between 8.8% and 19.0% more likely to be adopted in their first week compared to older dogs.
5.3. Practical Example 7: Alzheimer’s in Men and Women
How much more likely are women than men over 65 to develop Alzheimer’s? Among 893 men, 96 developed Alzheimer’s, and among 1129 women, 238 developed the disease. Calculate a 95% confidence interval.
-
Step 1: Calculate the Sample Proportions
- (hat{p}_{men} = frac{96}{893} approx 0.1075)
- (hat{p}_{women} = frac{238}{1129} approx 0.2108)
-
Step 2: Calculate the Difference in Sample Proportions
- (hat{p}_{women} – hat{p}_{men} = 0.2108 – 0.1075 = 0.1033)
-
Step 3: Determine the Critical Value
- For a 95% confidence level, the critical value (z = 1.96).
-
Step 4: Calculate the Standard Error
- Standard Error = (sqrt{frac{hat{p}_{men}(1-hat{p}_{men})}{n_{men}} + frac{hat{p}_{women}(1-hat{p}_{women})}{n_{women}}})
- Standard Error = (sqrt{frac{0.1075(1-0.1075)}{893} + frac{0.2108(1-0.2108)}{1129}})
- Standard Error = (sqrt{frac{0.1075(0.8925)}{893} + frac{0.2108(0.7892)}{1129}})
- Standard Error = (sqrt{frac{0.0959}{893} + frac{0.1664}{1129}})
- Standard Error = (sqrt{0.000107 + 0.000147})
- Standard Error = (sqrt{0.000254})
- Standard Error ≈ 0.0159
-
Step 5: Calculate the Margin of Error
- Margin of Error = (z cdot) Standard Error
- Margin of Error = (1.96 cdot 0.0159)
- Margin of Error ≈ 0.0312
-
Step 6: Calculate the Confidence Interval
- Confidence Interval = (Difference in Sample Proportions) ± Margin of Error
- Confidence Interval = (0.1033 pm 0.0312)
- Lower bound: (0.1033 – 0.0312 = 0.0721)
- Upper bound: (0.1033 + 0.0312 = 0.1345)
-
Result
- With 95% confidence, women over 65 are between 7.2% and 13.5% more likely to develop Alzheimer’s than men over 65.
6. Common Pitfalls and How to Avoid Them
6.1. Sample Size Issues
Small sample sizes can lead to unreliable results. Ensure that your samples are large enough to provide sufficient statistical power.
6.2. Non-Random Sampling
Using non-random samples can introduce bias. Always use random sampling techniques to ensure that your sample is representative of the population.
6.3. Violation of Independence
If the samples are not independent, the assumptions of the test are violated. Ensure that the two samples do not influence each other.
6.4. Misinterpreting P-values
A small p-value does not necessarily mean the effect is large or important, only that it is statistically significant. Consider the practical significance of the results.
6.5. Ignoring Confidence Intervals
Relying solely on hypothesis tests can be misleading. Confidence intervals provide valuable information about the range of possible values for the true difference in proportions.
7. Leveraging Technology for Comparing Proportions
Statistical software packages and online calculators can greatly simplify the process of comparing proportions. These tools automate calculations, provide accurate p-values, and generate confidence intervals, allowing you to focus on interpreting the results.
7.1. Using Statistical Software
Programs like SPSS, R, and SAS offer functions for performing hypothesis tests and constructing confidence intervals for proportions. These packages provide detailed output and diagnostic tools.
7.2. Online Calculators
Many websites offer free online calculators for comparing proportions. These tools are easy to use and require only basic input data.
8. Case Studies: Real-World Applications
8.1. Marketing Campaign Effectiveness
A company runs two different marketing campaigns to promote a new product. Campaign A results in a 15% conversion rate from website visits to sales, while Campaign B results in a 12% conversion rate. By comparing these proportions, the company can determine which campaign is more effective and allocate resources accordingly.
8.2. Healthcare Outcomes
A hospital compares the proportion of patients who develop infections after surgery under two different protocols. Protocol X results in a 5% infection rate, while Protocol Y results in a 3% infection rate. Comparing these proportions helps the hospital identify the better protocol and improve patient outcomes.
8.3. Educational Interventions
A school district compares the proportion of students who pass a standardized test after implementing two different teaching methods. Method 1 results in a 70% pass rate, while Method 2 results in an 80% pass rate. Comparing these proportions helps the district identify the more effective teaching method.
9. The Role of COMPARE.EDU.VN in Comparative Analysis
COMPARE.EDU.VN serves as a valuable resource for individuals and professionals seeking to make informed decisions through comparative analysis. It provides comprehensive comparisons across various domains, including:
- Product Comparisons: Detailed analyses of different products, highlighting their features, advantages, and disadvantages.
- Service Evaluations: Assessments of various services, helping users choose the best option based on their needs.
- Educational Resources: Comparisons of different educational programs, courses, and institutions.
By leveraging COMPARE.EDU.VN, users can gain access to reliable, data-driven insights that facilitate better decision-making.
Alternative Text: Comparison of features between educational programs, showing key differences in curriculum and outcomes.
10. FAQs About Comparing Proportions
10.1. What does comparing proportions mean?
Comparing proportions involves statistically assessing whether the differences observed between two or more proportions are significant, indicating a real difference in the populations from which the samples were drawn.
10.2. Why is comparing proportions important in data analysis?
Comparing proportions helps in making informed decisions, validating hypotheses, optimizing strategies, and identifying meaningful differences that are not due to chance.
10.3. What are the assumptions that must be met when comparing proportions?
The assumptions include having independent random samples, sufficient successes and failures in each sample, and a population size that is at least ten to twenty times larger than the sample size.
10.4. How is the pooled proportion calculated?
The pooled proportion is calculated by adding the number of successes in both samples and dividing by the total number of observations in both samples, providing an estimate of the common population proportion.
10.5. What does the test statistic (z-score) indicate in comparing proportions?
The test statistic (z-score) measures how many standard errors the observed difference between sample proportions is from the null hypothesis, helping to determine the statistical significance of the difference.
10.6. What does the p-value tell us in hypothesis testing for proportions?
The p-value indicates the probability of observing a test statistic as extreme as, or more extreme than, the one calculated, assuming the null hypothesis is true. A small p-value suggests strong evidence against the null hypothesis.
10.7. How is the confidence interval for the difference between two proportions interpreted?
If the confidence interval contains zero, it suggests no significant difference between the population proportions. If it does not contain zero, it suggests a significant difference, with the sign indicating the direction of the difference.
10.8. What are common pitfalls to avoid when comparing proportions?
Common pitfalls include sample size issues, non-random sampling, violation of independence, misinterpreting p-values, and ignoring confidence intervals.
10.9. How can technology assist in comparing proportions?
Statistical software packages and online calculators automate calculations, provide accurate p-values, and generate confidence intervals, making the process more efficient and reliable.
10.10. Where can I find reliable comparisons and detailed analyses to help with decision-making?
COMPARE.EDU.VN offers comprehensive comparisons across various domains, including product comparisons, service evaluations, and educational resources, providing reliable, data-driven insights.
11. Conclusion: Making Informed Decisions with Proportions
Comparing proportions is a powerful tool for making informed decisions across various fields. By understanding the underlying principles, applying appropriate statistical techniques, and avoiding common pitfalls, you can draw meaningful conclusions from data and optimize your strategies.
Ready to make more informed decisions? Visit COMPARE.EDU.VN today to access comprehensive comparisons and detailed analyses across a wide range of products, services, and educational resources. Our platform provides the data-driven insights you need to choose the best options for your specific needs and goals.
Contact us at:
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
WhatsApp: +1 (626) 555-9090
Website: COMPARE.EDU.VN
Start making smarter choices with compare.edu.vn.