How to Compare Numbers in Scientific Notation Easily

Comparing numbers in scientific notation can seem daunting, but it’s a straightforward process once you understand the basics. COMPARE.EDU.VN is here to simplify this task, offering clear explanations and practical examples to help you master the skill. With our comprehensive guide, you’ll learn how to quickly determine which number is larger or smaller, regardless of the exponent or coefficient. Whether you are dealing with positive or negative numbers, standard or scientific notation, we have got you covered with techniques that allow for efficient number comparison and magnitude estimation.

1. Understanding Scientific Notation

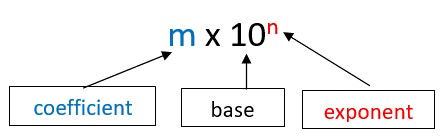
Scientific notation, also known as standard form or standard index form, is a method of expressing very large or very small numbers in a compact and manageable way. It is widely used in science, engineering, and mathematics to simplify calculations and comparisons. The general form of a number in scientific notation is:

m x 10ⁿ

Where:

• m is the coefficient (or significand), which is a real number with an absolute value between 1 (inclusive) and 10 (exclusive), meaning 1 ≤ |m| < 10.
• 10 is the base.
• n is the exponent (or power of 10), which is an integer. It can be positive, negative, or zero.

This notation helps in handling numbers that would otherwise be cumbersome to write out in full.

1.1. Components of Scientific Notation

Let’s break down the components of a scientific notation expression.

• Coefficient (m): The coefficient is a number between 1 and 10 (excluding 10). It provides the significant digits of the number. For example, in 3.14 x 10⁵, the coefficient is 3.14.
• Base (10): The base is always 10 in scientific notation. It indicates that the number is expressed as a power of 10.
• Exponent (n): The exponent is an integer that determines the magnitude of the number. A positive exponent indicates a large number, while a negative exponent indicates a small number. For example, in 2.7 x 10⁴, the exponent is 4, meaning the number is 2.7 multiplied by 10,000.

1.2. Examples of Numbers in Scientific Notation

Here are some examples of numbers correctly written in scientific notation:

• 2.7 x 10⁴
• -8.2 x 10^-2
• 5.1274 x 10⁰
• 9 x 10¹⁵
• -8.7 x 10^-8

And here are some examples of numbers that are not written in scientific notation:

• 273 x 10⁷ (Coefficient is greater than 10)
• 0.7 x 10³ (Coefficient is less than 1)
• 8 x 2⁹ (Base needs to be 10)
• 7.328 x 1000 (Needs an exponent on the base 10)
• -0.3 x 10^-2 (Coefficient is less than 1)

2. Why Use Scientific Notation?

Scientific notation offers several advantages, especially when dealing with very large or very small numbers:

• Conciseness: It simplifies the representation of numbers, making them easier to write and read. For example, the number 3,000,000,000 can be written as 3 x 10⁹.
• Clarity: It clearly indicates the magnitude of a number. The exponent tells you how many places to move the decimal point to get the number in standard notation.
• Ease of Comparison: It makes it easier to compare numbers of different magnitudes. By comparing the exponents, you can quickly determine which number is larger or smaller.
• Simplified Calculations: It simplifies calculations involving very large or very small numbers. Multiplication and division become easier when numbers are expressed in scientific notation.
• Standardization: It provides a standard format for expressing numbers, which is universally recognized in scientific and technical fields.

3. Steps to Compare Numbers in Scientific Notation

To effectively compare numbers in scientific notation, follow these steps:

1. Compare the Exponents: First, compare the exponents (the powers of 10). The number with the larger exponent is generally the larger number.
2. If Exponents Are Equal, Compare the Coefficients: If the exponents are the same, compare the coefficients (the numbers in front of the powers of 10). The number with the larger coefficient is the larger number.
3. Consider Negative Signs: If one or both numbers are negative, remember that the number closer to zero is larger.

Let’s explore these steps with examples to illustrate how they work in practice.

4. Comparing Positive Numbers in Scientific Notation

Comparing positive numbers in scientific notation is relatively straightforward. The key is to first look at the exponents and then, if necessary, compare the coefficients.

4.1. Case 1: Different Exponents

When comparing two positive numbers in scientific notation, if the exponents are different, the number with the larger exponent is the larger number. This holds true whether the exponents are positive or negative.

• If b > d, then a x 10^b > c x 10^d
• If b < d, then a x 10^b < c x 10^d

Examples:

• 1. 48 x 10³ is smaller than 4.82 x 10⁵ because the first number has an exponent of 3, and the second number has a larger exponent of 5.
• 2. 02 x 10¹² is larger than 9.1 x 10⁸ because the first number has an exponent of 12, and the second number has a smaller exponent of 8.
• 3. 2 x 10^-2 is larger than 1.78 x 10^-4 because when comparing the exponents, -2 > -4.
• 4. 45 x 10^-2 is smaller than 2.8 x 10⁰ because when comparing the exponents, -2 < 0.

4.2. Case 2: Same Exponents

If both numbers have the same exponent, the number with the larger coefficient is the larger number.

• If b = d, then if a > c, a x 10^b > c x 10^d

Example:

• 3.2 x 10⁵ is larger than 2.9 x 10⁵ because both numbers have the same exponent, and 3.2 > 2.9.

5. Comparing Negative Numbers in Scientific Notation

When comparing negative numbers, remember that the number closest to zero is the larger number. This principle applies to numbers in scientific notation as well.

5.1. Case 1: Different Exponents

When comparing two negative numbers in scientific notation, the number with the smaller exponent is the larger number because it is the least negative. This is true whether the exponents are positive or negative.

Examples:

• -1.48 x 10³ is larger than -4.82 x 10⁵ because the first number has a smaller exponent of 3, and the second number has an exponent of 5.
• -3.02 x 10¹² is smaller than -9.1 x 10⁸ because the first number has an exponent of 12, and the second number has a smaller exponent of 8.
• -5.2 x 10^-2 is smaller than -1.78 x 10^-4 because when comparing the exponents, -2 > -4.
• -8.45 x 10^-2 is larger than -2.8 x 10⁰ because when comparing the exponents, -2 < 0.

5.2. Case 2: Same Exponents

If both numbers have the same exponent, the negative number with the smaller coefficient is the larger number.

Example:

• -3.2 x 10⁵ is smaller than -2.9 x 10⁵ because both numbers have the same exponent, and -3.2 < -2.9.

6. Comparing Negative and Positive Numbers in Scientific Notation

The rule here is simple: any positive number is always larger than any negative number. This applies regardless of the exponents or coefficients.

Examples:

• -2.6 x 10³ is smaller than 1.2 x 10² because a positive number is always greater than a negative number.
• 5.8 x 10^-4 is larger than -7 x 10⁵ because a positive number is always greater than a negative number.
• -2.6 x 10^-2 is smaller than 1.4 x 10^-8 because a positive number is always greater than a negative number.

7. Comparing Numbers in Scientific Notation with Numbers in Standard Notation

When comparing a number in scientific notation to a number in standard notation, you have two options:

1. Convert the number in scientific notation to standard notation.
2. Convert the number in standard notation to scientific notation.

The best approach depends on the specific numbers you’re comparing. For very large or very small numbers, converting to scientific notation is often easier due to the compact representation.

Examples:

• Example 1:
  • Compare 3.4 x 10³ and 3,000.
  • Convert 3.4 x 10³ to standard notation: 3.4 x 1000 = 3,400.
  • Since 3,400 > 3,000, 3.4 x 10³ is larger than 3,000.
• Example 2:
  • Compare 5.8 x 10^-2 and 0.06.
  • Convert 5.8 x 10^-2 to standard notation: 5.8 ÷ 100 = 0.058.
  • Since 0.058 < 0.06, 5.8 x 10^-2 is smaller than 0.06.
• Example 3:
  • Compare 2.6 x 10⁹ and 300,000,000.
  • Convert 300,000,000 to scientific notation: 3 x 10⁸.
  • Since 2.6 x 10⁹ has a larger exponent than 3 x 10⁸, 2.6 x 10⁹ is larger than 300,000,000.

8. Worked Examples

Let’s go through some worked examples to solidify your understanding of comparing numbers in scientific notation.

8.1. Example 1

Problem: Which of these numbers is larger: 4.8 x 10⁵ or 8.2 x 10³?

Solution:

1. Identify the exponents:
   • 4.8 x 10⁵ has an exponent of 5.
   • 8.2 x 10³ has an exponent of 3.
2. Compare the exponents:
   • Since 5 > 3, 4.8 x 10⁵ is larger than 8.2 x 10³.

Answer: 4.8 x 10⁵ > 8.2 x 10³

8.2. Example 2

Problem: Put these three numbers in order from smallest to largest: 3.4 x 10^-1, 1.7 x 10¹, and 7.8 x 10^-2.

Solution:

1. Identify the exponents:
   • 3.4 x 10^-1 has an exponent of -1.
   • 1.7 x 10¹ has an exponent of 1.
   • 7.8 x 10^-2 has an exponent of -2.
2. Order the exponents from smallest to largest:
   • The correct order for the exponents is: -2, -1, 1.
3. Arrange the numbers according to the order of their exponents:
   • The correct order from smallest to largest is: 7.8 x 10^-2, 3.4 x 10^-1, and 1.7 x 10¹.

Answer: 7.8 x 10^-2 < 3.4 x 10^-1 < 1.7 x 10¹

8.3. Example 3

Problem: Put these three numbers in order from smallest to largest: -9.3 x 10^-1, -3.1 x 10⁶, and -2.5 x 10³.

Solution:

1. Identify the exponents:
   • -9.3 x 10^-1 has an exponent of -1.
   • -3.1 x 10⁶ has an exponent of 6.
   • -2.5 x 10³ has an exponent of 3.
2. Order the exponents from smallest to largest:
   • The correct order for the exponents is: -1, 3, 6.
3. Remember the rule for negative numbers:
   • With negative numbers, the smaller the absolute value, the larger the number. Therefore, the number with the smallest exponent is the largest.
4. Arrange the numbers accordingly:
   • The correct order from smallest to largest is: -3.1 x 10⁶, -2.5 x 10³, and -9.3 x 10^-1.

Answer: -3.1 x 10⁶ < -2.5 x 10³ < -9.3 x 10^-1

8.4. Example 4

Problem: Put these three numbers in order from smallest to largest: 2.8 x 10^-2, -4 x 10^-3, and -6.5 x 10^-1.

Solution:

1. Identify the positive and negative numbers:
   • 2.8 x 10^-2 is positive.
   • -4 x 10^-3 is negative.
   • -6.5 x 10^-1 is negative.
2. Remember the rule:
   • The positive number will always be the largest.
3. Order the negative numbers:
   • -4 x 10^-3 has an exponent of -3.
   • -6.5 x 10^-1 has an exponent of -1.
4. Apply the rule for negative numbers:
   • The smaller the absolute value, the bigger the number.
   • Therefore, -4 x 10^-3 is larger than -6.5 x 10^-1.
5. Arrange all the numbers accordingly:
   • The correct order from smallest to largest is: -6.5 x 10^-1, -4 x 10^-3, and 2.8 x 10^-2.

Answer: -6.5 x 10^-1 < -4 x 10^-3 < 2.8 x 10^-2

9. Practice Worksheets

To help you further practice comparing numbers in scientific notation, here are some types of worksheets you can use:

9.1. Comparing Two Numbers in Scientific Notation

These worksheets focus on comparing two numbers at a time, helping you practice the basic skill of determining which number is larger or smaller.

• Worksheet 1: Comparing positive numbers in scientific notation with positive exponents only.
• Worksheet 2: Comparing positive numbers in scientific notation with both positive and negative exponents.
• Worksheet 3: Comparing both positive and negative numbers with positive and negative exponents.

9.2. Ordering Numbers in Scientific Notation

These worksheets require you to order a set of numbers from smallest to largest, reinforcing your understanding of relative magnitudes.

• Worksheet 1A: Ordering positive numbers in scientific notation with positive exponents only.
• Worksheet 2A: Ordering positive numbers in scientific notation with both positive and negative exponents.
• Worksheet 3A: Ordering both positive and negative numbers with positive and negative exponents.

9.3. Ordering Numbers in Scientific Notation and Standard Notation

These worksheets combine numbers in both scientific and standard notation, challenging you to convert between the two forms and compare them effectively.

• Worksheet 1B: Ordering positive numbers in both standard and scientific notation with positive exponents only.
• Worksheet 2B: Ordering positive numbers in both standard and scientific notation with both positive and negative exponents.
• Worksheet 3B: Ordering both positive and negative numbers in standard and scientific notation with positive and negative exponents.

10. Additional Resources

To further enhance your understanding and skills in scientific notation, consider exploring these additional resources.

10.1. Standard Notation and Scientific Notation Support Pages

Dedicated support pages that provide detailed explanations and worked examples can be invaluable. These pages often include practice worksheets to test your knowledge.

10.2. Convert Scientific to Standard Notation Calculators

Online calculators can quickly convert numbers between scientific and standard notation. These tools are particularly useful for checking your work and handling complex conversions.

10.3. Number System Converters

Understanding different number systems (binary, octal, hexadecimal) can provide a broader perspective on numerical representation. Number system converters can help you explore these systems and their relationships to decimal notation.

10.4. Online Quizzes

Online quizzes offer a fun and interactive way to test your skills in comparing numbers in scientific notation. These quizzes provide instant feedback and can help you identify areas where you need more practice.

11. Common Mistakes to Avoid

When comparing numbers in scientific notation, be aware of these common mistakes:

• Forgetting the Rules for Negative Numbers: When comparing negative numbers, remember that the number closer to zero is larger. This is especially important when the numbers are in scientific notation.
• Ignoring the Exponents: Always start by comparing the exponents. The exponent determines the magnitude of the number, so it is the most important factor in the comparison.
• Not Converting to the Same Notation: When comparing a number in scientific notation to a number in standard notation, make sure to convert both numbers to the same notation before comparing them.
• Misinterpreting Negative Exponents: A negative exponent indicates a small number (a number between 0 and 1), not a negative number. Make sure you understand the meaning of negative exponents before comparing numbers.
• Comparing Coefficients Before Exponents: Always compare the exponents first. If the exponents are different, you don’t need to compare the coefficients.

12. Tips for Mastering Scientific Notation Comparisons

Here are some tips to help you master comparing numbers in scientific notation:

• Practice Regularly: The more you practice, the more comfortable you will become with comparing numbers in scientific notation. Use worksheets, online quizzes, and real-world examples to hone your skills.
• Understand the Basics: Make sure you have a solid understanding of what scientific notation is and how it works. Review the definitions of the coefficient, base, and exponent.
• Follow a Systematic Approach: Use a step-by-step approach when comparing numbers. Start by comparing the exponents, then compare the coefficients if necessary.
• Use Real-World Examples: Look for examples of scientific notation in real-world contexts, such as scientific measurements, engineering calculations, and financial data. This will help you see the practical applications of the concept.
• Check Your Work: Always check your work to make sure you have not made any mistakes. Use a calculator or online converter to verify your answers.

13. Real-World Applications of Comparing Numbers in Scientific Notation

Comparing numbers in scientific notation is not just an academic exercise. It has many practical applications in various fields:

• Science: Scientists use scientific notation to express and compare measurements of very large and very small quantities, such as the distances between stars, the sizes of atoms, and the masses of subatomic particles.
• Engineering: Engineers use scientific notation to express and compare values in their calculations, such as the strength of materials, the speed of light, and the power output of engines.
• Computer Science: Computer scientists use scientific notation to express and compare the sizes of data sets, the speeds of processors, and the capacities of storage devices.
• Finance: Financial analysts use scientific notation to express and compare large sums of money, such as the national debt, the market capitalization of companies, and the value of investments.
• Everyday Life: Even in everyday life, scientific notation can be useful for understanding and comparing large numbers, such as population statistics, distances on maps, and the costs of major projects.

14. Addressing Customer Challenges

Many individuals face challenges when comparing different options objectively and comprehensively. They often lack detailed, reliable information to make informed decisions. The abundance of information can be overwhelming, making it difficult to focus on essential factors. Visual comparisons and insights from experienced users are highly valued.

COMPARE.EDU.VN aims to address these challenges by providing detailed, unbiased comparisons of various products, services, and ideas. Our platform clearly outlines the advantages and disadvantages of each option, compares features, specifications, prices, and other critical factors. We also offer user reviews and expert opinions to help users make informed decisions that best suit their needs and budgets.

15. COMPARE.EDU.VN: Your Partner in Informed Decision-Making

At COMPARE.EDU.VN, we understand the importance of making informed decisions. Whether you are comparing academic programs, consumer products, or professional methodologies, our platform offers the comprehensive, objective comparisons you need.

We strive to provide:

• Detailed Comparisons: Comprehensive analyses of various options.
• Objective Evaluations: Unbiased assessments of pros and cons.
• User Reviews: Real-world insights from other users.
• Expert Opinions: Professional analysis to guide your choices.

16. Frequently Asked Questions (FAQ)

Here are some frequently asked questions about comparing numbers in scientific notation:

1. What is scientific notation?
   • Scientific notation is a way of expressing very large or very small numbers in a compact form, using a coefficient and a power of 10.
2. Why use scientific notation?
   • It simplifies the representation, comparison, and calculation of very large or very small numbers.
3. How do you write a number in scientific notation?
   • Write the number as a coefficient between 1 and 10, multiplied by a power of 10.
4. How do you compare two numbers in scientific notation?
   • First, compare the exponents. If the exponents are the same, compare the coefficients.
5. What if the exponents are negative?
   • For positive numbers, the larger the exponent, the larger the number. For negative numbers, the smaller the exponent, the larger the number (closer to zero).
6. How do you compare a number in scientific notation with a number in standard notation?
   • Convert both numbers to the same notation before comparing them.
7. What is the significance of the coefficient in scientific notation?
   • The coefficient provides the significant digits of the number.
8. Can the exponent be zero?
   • Yes, an exponent of zero means the number is equal to the coefficient.
9. How do you handle negative numbers in scientific notation?
   • The same rules apply, but remember that the negative number closer to zero is larger.
10. Where can I find more resources to practice comparing numbers in scientific notation?
    • COMPARE.EDU.VN offers detailed guides, practice worksheets, and external links to further enhance your understanding.

17. Call to Action

Ready to make informed decisions with confidence? Visit COMPARE.EDU.VN today to explore our comprehensive comparisons and discover the best choices for your needs. Whether you’re evaluating educational programs, products, or services, COMPARE.EDU.VN is your trusted resource for objective and detailed comparisons. Don’t struggle with overwhelming information – let us help you make the right choice.

Contact Us:

• Address: 333 Comparison Plaza, Choice City, CA 90210, United States
• WhatsApp: +1 (626) 555-9090
• Website: COMPARE.EDU.VN

18. Conclusion

Comparing numbers in scientific notation is a valuable skill with applications in various fields. By understanding the basic principles and following a systematic approach, you can easily compare numbers of any magnitude. Whether you are a student, a professional, or simply someone who wants to make informed decisions, compare.edu.vn is here to provide the resources and support you need. Visit our website today to explore our comprehensive comparisons and discover the best choices for your needs.