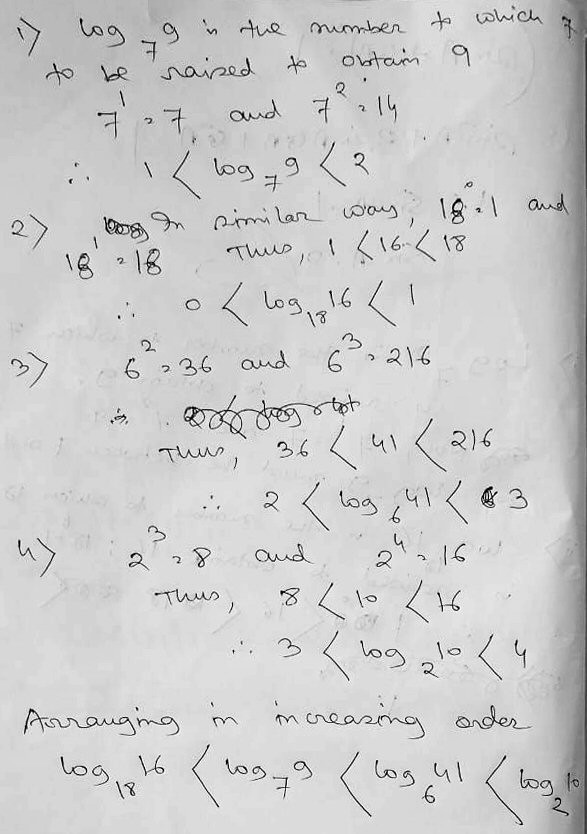Comparing logarithms with different bases can be challenging. This guide provides various strategies and examples to help you master this skill. We will explore techniques like estimation, the change of base formula, and visualization through graphs.
Estimating Logarithms Using Integer Bounds
A simple yet effective method for comparing logarithms is to estimate their values by finding the integers they lie between. Consider log₇(9). Since 7¹ = 7 and 7² = 49, and 7 < 9 < 49, we know that 1 < log₇(9) < 2. This technique allows for quick comparison when numbers are strategically chosen. For instance, to estimate log₁₈(16), recognize that 18⁰ = 1 and 18¹ = 18, and 1 < 16 < 18, meaning 0 < log₁₈(16) < 1. This clarifies that log₁₈(16) < log₇(9).
Utilizing the Change of Base Formula
The change of base formula, logb(x) = loga(x) / loga(b), offers a powerful way to compare logarithms. By converting logarithms to a common base, comparisons become straightforward. For example, to compare log1/2(4/3) and log2(1/3), we can rewrite them using base 10:
- log1/2(4/3) = log(4/3) / log(1/2) = log(4/3) / -log(2)
- log2(1/3) = log(1/3) / log(2) = -log(3) / log(2)
Since log(4/3) and log(2) are positive, log1/2(4/3) is negative. Similarly, log2(1/3) is also negative. To determine which is larger, further analysis or different techniques might be needed.
Visualizing Logarithms with Graphs
Understanding the graphical representation of logarithmic functions can provide valuable insights for comparison. Logarithms with bases greater than 1 have increasing curves, while those with bases between 0 and 1 have decreasing curves.
This visualization aids in quickly determining the sign of a logarithm and comparing magnitudes. For example, log1/2(4/3) falls on a decreasing curve, and since 4/3 > 1, the result is negative. log2/3(0.8) also falls on a decreasing curve, but since 0.8 < 1, the result is positive.
Comparing Fractional Logarithms
Consider the challenge of comparing log1/2(2/3) and log2/3(1/2). Using the change of base formula with base 2:
- log1/2(2/3) = (log2(2) – log2(3)) / -log2(2) = log2(3) – 1
- log2/3(1/2) = -log2(2) / (log2(2) – log2(3)) = 1 / (1 – log2(3))
Since 1 < log2(3) < 2, then 0 < log2(3) – 1 < 1. Consequently, log2/3(1/2) > 1, making it larger than log1/2(2/3).
Conclusion
Comparing logarithms can be approached through various techniques. By understanding estimation, utilizing the change of base formula, and visualizing logarithmic graphs, you can effectively compare logarithms with different bases and solve complex logarithmic problems. Remember to carefully consider the properties of logarithms and choose the method that best suits the problem at hand.