Comparing inequalities can be tricky, but COMPARE.EDU.VN offers solutions. Discover the strategies, methods, and practical examples for comparing inequalities effectively. Explore techniques for visualizing inequality, understanding different inequality metrics, and applying these concepts in real-world scenarios, with a focus on promoting fair comparisons and informed decision-making.
1. Understanding the Basics of Inequalities
Inequalities are mathematical expressions that show the relative order of two values. They use symbols like < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to). Grasping these symbols and their meanings is the first step in understanding How To Compare Inequalities effectively. Inequalities play a crucial role in various fields, from economics to engineering, making their comparison a valuable skill.
1.1. Defining Inequality and Its Significance
Inequality, in a broad sense, represents an uneven distribution or disparity. In mathematics, it refers to a statement that two values are not equal. In economics, it can refer to the distribution of income or wealth. Understanding different types of inequalities is vital when considering inequality assessment.
1.2. Different Types of Inequalities
There are several types of inequalities, each with its own nuances. These include:
-
Strict Inequalities: Use < or > to indicate that one value is strictly less than or greater than another.
-
Non-Strict Inequalities: Use ≤ or ≥ to indicate that one value is less than or equal to, or greater than or equal to, another.
-
Absolute Value Inequalities: Involve absolute values, requiring careful consideration of both positive and negative cases.
-
Compound Inequalities: Combine two or more inequalities using “and” or “or.”
1.3. Properties of Inequalities
Understanding the properties of inequalities is essential for manipulating and comparing them. Key properties include:
-
Addition Property: Adding the same value to both sides of an inequality preserves the inequality.
-
Subtraction Property: Subtracting the same value from both sides of an inequality preserves the inequality.
-
Multiplication Property: Multiplying both sides of an inequality by a positive value preserves the inequality. Multiplying by a negative value reverses the inequality.
-
Division Property: Dividing both sides of an inequality by a positive value preserves the inequality. Dividing by a negative value reverses the inequality.
-
Transitive Property: If a > b and b > c, then a > c.
2. Methods for Comparing Inequalities
Several methods can be employed when considering how to compare inequalities. These range from graphical approaches to analytical techniques, each offering unique insights.
2.1. Graphical Methods
Graphical methods provide a visual way to compare inequalities. This approach is particularly useful when dealing with linear inequalities or systems of inequalities.
2.1.1. Plotting Inequalities on a Number Line
For single-variable inequalities, plotting the solution set on a number line can be very effective. This involves:
- Drawing a number line.
- Identifying the boundary point (the value where the inequality becomes an equality).
- Using an open circle for strict inequalities (< or >) and a closed circle for non-strict inequalities (≤ or ≥).
- Shading the region that satisfies the inequality.
2.1.2. Graphing Linear Inequalities
For two-variable linear inequalities, graphing involves:
- Treating the inequality as an equation and graphing the corresponding line.
- Using a solid line for non-strict inequalities (≤ or ≥) and a dashed line for strict inequalities (< or >).
- Shading the region that satisfies the inequality. To determine which region to shade, test a point (e.g., (0,0)) in the original inequality.
2.2. Analytical Methods
Analytical methods involve using algebraic techniques to compare inequalities. These methods are more suitable for complex inequalities or when a precise comparison is needed.
2.2.1. Using Transitive Property for Comparisons
The transitive property is a powerful tool for comparing multiple inequalities. If you know that a > b and b > c, you can conclude that a > c without needing to directly compare a and c.
2.2.2. Algebraic Manipulation to Simplify Inequalities
Simplifying inequalities through algebraic manipulation can make comparisons easier. This might involve:
- Combining like terms.
- Factoring expressions.
- Using properties of inequalities to isolate variables.
2.2.3. Case-by-Case Analysis for Absolute Value Inequalities
Absolute value inequalities require careful consideration of different cases:
- If |x| < a, then -a < x < a.
- If |x| > a, then x < -a or x > a.
By analyzing each case separately, you can determine the solution set and compare it with other inequalities.
2.3. Using Technology for Comparing Inequalities
Various software tools and online calculators can assist in comparing inequalities, especially when dealing with complex expressions or large datasets.
2.3.1. Software Tools for Graphing and Analysis
Software like Mathematica, MATLAB, and GeoGebra can be used to graph inequalities, solve systems of inequalities, and perform complex analytical calculations.
2.3.2. Online Calculators and Solvers
Many online calculators and solvers are available for solving inequalities. These tools can quickly provide solutions and graphical representations, making comparisons more efficient.
3. Factors Affecting Inequality Comparisons
Several factors can influence how inequalities are compared. These include the context of the inequality, the data being used, and the metrics being considered.
3.1. Contextual Factors
The context in which inequalities are being compared is crucial. For example, comparing income inequality in different countries requires understanding their economic systems, social policies, and historical backgrounds.
3.1.1. Economic Systems and Policies
Different economic systems and policies can significantly impact inequality levels. Comparing inequalities between countries with different systems requires careful consideration of these factors.
3.1.2. Social and Historical Backgrounds
Social and historical factors can also influence inequality. Historical events, cultural norms, and social structures can shape the distribution of resources and opportunities.
3.2. Data Quality and Availability
The quality and availability of data can greatly affect inequality comparisons. Data from different sources may have varying levels of accuracy and completeness, which can impact the reliability of the comparisons.
3.2.1. Sources of Data
Common sources of data for inequality comparisons include:
-
Household surveys
-
Tax records
-
National accounts
Each of these sources has its own strengths and limitations, which should be considered when interpreting the results.
3.2.2. Accuracy and Completeness
The accuracy and completeness of data are critical for reliable comparisons. Inaccurate or incomplete data can lead to biased results and misleading conclusions.
3.3. Choosing the Right Metrics
Selecting the appropriate metrics is essential for comparing inequalities effectively. Different metrics capture different aspects of inequality, and the choice of metric can influence the results.
3.3.1. Common Inequality Metrics
Some common inequality metrics include:
-
Gini Coefficient: Measures the extent to which the distribution of income or wealth among individuals or households within an economy deviates from a perfectly equal distribution.
-
Income or Wealth Ratios (e.g., 90/10 ratio): Compares the income or wealth of the top 10% to the bottom 10% of the population.
-
Palma Ratio: Compares the income share of the top 10% to the bottom 40% of the population.
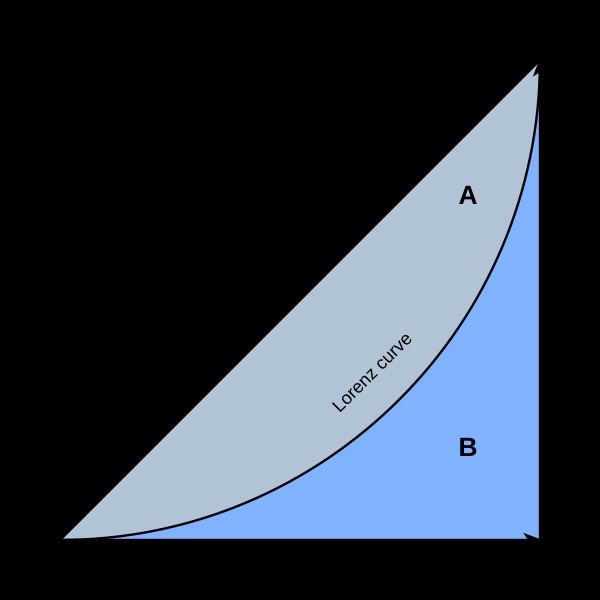Visual representation of the Gini coefficient on a Lorenz curve
3.3.2. Advantages and Disadvantages of Each Metric
Each inequality metric has its own advantages and disadvantages. For example, the Gini coefficient is sensitive to changes in the middle of the distribution but less sensitive to changes at the extremes. Income ratios, on the other hand, focus on the extremes but may not capture changes in the middle.
4. Real-World Applications of Inequality Comparisons
Comparing inequalities has numerous real-world applications, ranging from policy-making to investment decisions. Understanding these applications can highlight the importance of effective inequality comparison.
4.1. Policy-Making
Inequality comparisons are essential for policy-making. Governments use these comparisons to assess the impact of policies, identify areas where intervention is needed, and design policies to promote greater equality.
4.1.1. Assessing the Impact of Policies
By comparing inequality levels before and after the implementation of a policy, governments can assess the policy’s impact and make adjustments as needed.
4.1.2. Identifying Areas Where Intervention Is Needed
Inequality comparisons can help identify specific areas or groups where intervention is most needed. For example, if a particular region or demographic group has significantly higher inequality levels, targeted policies can be designed to address the issue.
4.2. Investment Decisions
Investors also use inequality comparisons to inform their decisions. Understanding inequality trends can help investors identify potential risks and opportunities in different markets.
4.2.1. Identifying Potential Risks and Opportunities
High levels of inequality can indicate social and economic instability, which can pose risks for investors. On the other hand, growing middle classes in some countries can create opportunities for investment in consumer goods and services.
4.2.2. Understanding Market Dynamics
Inequality can also affect market dynamics. For example, in highly unequal societies, consumer demand may be concentrated among a small elite, which can impact the types of products and services that are successful.
4.3. Social and Economic Research
Inequality comparisons are fundamental to social and economic research. Researchers use these comparisons to study the causes and consequences of inequality, and to develop theories and models to explain inequality trends.
4.3.1. Studying the Causes and Consequences of Inequality
By comparing inequality levels across different countries, regions, and time periods, researchers can identify factors that contribute to inequality and understand its effects on various social and economic outcomes.
4.3.2. Developing Theories and Models
Inequality comparisons can also inform the development of theories and models to explain inequality trends. These theories and models can then be used to make predictions about future inequality levels and to evaluate the potential impact of policies and interventions.
5. Common Pitfalls in Comparing Inequalities
Despite the importance of comparing inequalities, there are several common pitfalls to avoid. Being aware of these pitfalls can help ensure that comparisons are accurate and meaningful.
5.1. Using Incompatible Data Sets
Using incompatible data sets is a common pitfall in inequality comparisons. Data sets may differ in terms of their definitions, methodologies, and coverage, which can lead to misleading results.
5.1.1. Differences in Definitions and Methodologies
Different data sets may use different definitions of income, wealth, and other key variables. They may also employ different methodologies for data collection and processing. These differences can make it difficult to compare inequality levels across data sets.
5.1.2. Inconsistent Coverage
Data sets may also have inconsistent coverage. For example, some data sets may only cover certain regions or demographic groups, while others may have broader coverage. Comparing inequality levels across data sets with inconsistent coverage can lead to biased results.
5.2. Ignoring Contextual Differences
Ignoring contextual differences is another common pitfall in inequality comparisons. As discussed earlier, economic systems, social policies, and historical backgrounds can all influence inequality levels. Failing to account for these factors can lead to inaccurate comparisons.
5.2.1. Economic Systems
Different economic systems have different implications for inequality. For example, market-based economies may tend to have higher levels of inequality than centrally planned economies, although this is not always the case.
5.2.2. Social Policies
Social policies, such as progressive taxation and social welfare programs, can also affect inequality levels. Countries with more generous social policies tend to have lower levels of inequality.
5.3. Misinterpreting Inequality Metrics
Misinterpreting inequality metrics is another common pitfall. Each metric has its own strengths and limitations, and it is important to understand these when interpreting the results.
5.3.1. Understanding the Strengths and Limitations of Each Metric
As discussed earlier, different inequality metrics capture different aspects of inequality. For example, the Gini coefficient is sensitive to changes in the middle of the distribution, while income ratios focus on the extremes. Understanding these strengths and limitations is essential for interpreting the results accurately.
5.3.2. Avoiding Over-Reliance on a Single Metric
Relying too heavily on a single metric can also be misleading. It is often more informative to consider multiple metrics and to look for consistent patterns across different measures.
6. Advanced Techniques for Inequality Comparisons
For more in-depth analysis, several advanced techniques can be used to compare inequalities. These techniques provide more nuanced insights and can help address some of the limitations of simpler methods.
6.1. Decomposition Analysis
Decomposition analysis involves breaking down overall inequality into its component parts. This can help identify the factors that contribute most to inequality and can inform the design of targeted policies.
6.1.1. Decomposing Inequality by Income Source
One common approach is to decompose inequality by income source. This involves determining how much of overall inequality is due to differences in wages, salaries, profits, rents, and other sources of income.
6.1.2. Decomposing Inequality by Population Group
Another approach is to decompose inequality by population group. This involves determining how much of overall inequality is due to differences between groups (e.g., men vs. women, different racial or ethnic groups, different education levels) and how much is due to inequality within groups.
6.2. Counterfactual Analysis
Counterfactual analysis involves comparing actual inequality levels to what they would have been under different scenarios. This can help assess the impact of specific policies or events on inequality.
6.2.1. Simulating the Impact of Policy Changes
One application of counterfactual analysis is to simulate the impact of policy changes. For example, one could compare actual inequality levels to what they would have been if a different tax system had been in place.
6.2.2. Assessing the Impact of Economic Shocks
Counterfactual analysis can also be used to assess the impact of economic shocks, such as recessions or financial crises, on inequality.
6.3. Statistical Modeling
Statistical modeling involves using statistical techniques to analyze inequality trends and to identify the factors that are most strongly associated with inequality.
6.3.1. Regression Analysis
Regression analysis is a common statistical technique used to analyze the relationship between inequality and other variables. This can help identify the factors that are most strongly associated with inequality.
6.3.2. Time Series Analysis
Time series analysis involves analyzing inequality trends over time. This can help identify patterns and cycles in inequality levels and can inform predictions about future inequality trends.
7. Visualizing Inequality: Tools and Techniques
Visualizing inequality is crucial for understanding and communicating complex data. Effective visualizations can reveal patterns and trends that might be missed in numerical data alone.
7.1. Lorenz Curves
Lorenz curves are a graphical representation of income or wealth distribution. They plot the cumulative percentage of total income or wealth held by the bottom x% of the population. The further the curve sags away from the line of perfect equality, the greater the inequality.
7.1.1. Constructing Lorenz Curves
To construct a Lorenz curve:
- Rank the population from lowest to highest income or wealth.
- Calculate the cumulative percentage of the population.
- Calculate the cumulative percentage of total income or wealth.
- Plot the cumulative percentage of the population on the x-axis and the cumulative percentage of income or wealth on the y-axis.
7.1.2. Interpreting Lorenz Curves
The closer the Lorenz curve is to the line of perfect equality, the more equal the distribution. The area between the Lorenz curve and the line of perfect equality represents the extent of inequality. This area is used to calculate the Gini coefficient.
7.2. Histograms and Density Plots
Histograms and density plots can be used to visualize the distribution of income or wealth. These plots show the frequency or density of different income or wealth levels.
7.2.1. Creating Histograms and Density Plots
To create histograms and density plots, divide the income or wealth range into intervals and count the number of individuals or households in each interval. Plot the intervals on the x-axis and the frequency or density on the y-axis.
7.2.2. Analyzing the Shape of Distributions
The shape of the distribution can provide insights into inequality. A more skewed distribution indicates higher inequality, with a longer tail on the right side representing higher incomes or wealth.
7.3. Interactive Data Visualization Tools
Interactive data visualization tools allow users to explore inequality data in a more dynamic and engaging way. These tools often provide features such as zooming, filtering, and customizable charts and graphs.
7.3.1. Tableau
Tableau is a powerful data visualization tool that allows users to create interactive dashboards and reports. It supports a wide range of chart types and data sources.
7.3.2. D3.js
D3.js is a JavaScript library for creating interactive data visualizations. It provides a high degree of flexibility and customization.
8. Case Studies: Comparing Inequalities Across Different Contexts
Examining case studies can provide practical insights into how to compare inequalities in different contexts. These examples illustrate the challenges and opportunities in comparing inequalities across countries, regions, and time periods.
8.1. Comparing Income Inequality in Developed vs. Developing Countries
Comparing income inequality in developed vs. developing countries reveals significant differences. Developed countries often have lower levels of income inequality due to more robust social safety nets and progressive taxation policies.
8.1.1. Factors Contributing to Differences
Factors contributing to differences include:
-
Economic Structures: Developed countries tend to have more diversified economies with higher-paying jobs.
-
Social Policies: Developed countries often have more generous social welfare programs and progressive taxation policies.
-
Education Levels: Developed countries typically have higher education levels, leading to better job opportunities and higher incomes.
8.1.2. Implications for Policy
Implications for policy include the need for developing countries to focus on economic diversification, strengthening social safety nets, and improving education levels to reduce income inequality.
8.2. Comparing Wealth Inequality Across Regions
Comparing wealth inequality across regions also reveals significant differences. Some regions have much higher levels of wealth inequality due to historical factors, economic policies, and social structures.
8.2.1. Historical Factors
Historical factors, such as colonialism and slavery, have had a lasting impact on wealth inequality in many regions.
8.2.2. Economic Policies
Economic policies, such as tax policies and regulations, can also affect wealth inequality.
8.2.3. Social Structures
Social structures, such as inheritance laws and social norms, can also influence wealth inequality.
8.3. Analyzing Trends in Inequality Over Time
Analyzing trends in inequality over time can provide insights into the factors that drive inequality and the impact of policies and events.
8.3.1. Long-Term Trends
Long-term trends in inequality reveal periods of increasing and decreasing inequality. These trends can be influenced by factors such as technological change, globalization, and policy changes.
8.3.2. Short-Term Fluctuations
Short-term fluctuations in inequality can be caused by economic shocks, such as recessions or financial crises.
9. The Role of COMPARE.EDU.VN in Facilitating Inequality Comparisons
COMPARE.EDU.VN is dedicated to providing comprehensive and objective comparisons of various topics, including inequality. Our platform offers a range of tools and resources to help users compare inequalities effectively.
9.1. Providing Access to Reliable Data
COMPARE.EDU.VN provides access to reliable data from various sources. We carefully vet our data sources to ensure accuracy and completeness.
9.2. Offering Tools for Visualization and Analysis
We offer a range of tools for visualizing and analyzing inequality data. Our interactive charts and graphs allow users to explore data in a dynamic and engaging way.
9.3. Promoting Informed Decision-Making
Our goal is to promote informed decision-making by providing users with the information and tools they need to compare inequalities effectively.
10. Future Directions in Inequality Comparisons
The field of inequality comparisons is constantly evolving. New data sources, methods, and tools are being developed to improve our understanding of inequality.
10.1. Incorporating New Data Sources
New data sources, such as satellite imagery and social media data, are being used to study inequality. These data sources can provide insights into aspects of inequality that are not captured by traditional data sources.
10.2. Developing New Methods
New methods, such as machine learning and artificial intelligence, are being developed to analyze inequality data. These methods can help identify patterns and relationships that are difficult to detect using traditional statistical techniques.
10.3. Addressing Data Gaps
Addressing data gaps is a critical challenge in inequality comparisons. Many countries lack reliable data on income and wealth, making it difficult to compare inequality levels across countries.
FAQ: Frequently Asked Questions About Comparing Inequalities
1. What is the Gini coefficient, and how is it used to compare inequalities?
The Gini coefficient is a measure of statistical dispersion intended to represent the income inequality or the wealth inequality within a nation or any group of people. It ranges from 0 to 1, where 0 expresses perfect equality and 1 expresses maximal inequality.
2. How do you compare income inequality between two different countries?
To compare income inequality between two countries, use standardized metrics like the Gini coefficient, income ratios (e.g., 90/10), and data from reliable sources such as the World Bank and the OECD. Consider economic policies, social structures, and historical factors.
3. What are some common data sources for comparing inequalities?
Common data sources include household surveys, tax records, and national accounts data. International organizations like the World Bank, the OECD, and the United Nations also provide valuable data.
4. Why is it important to use compatible data sets when comparing inequalities?
Using compatible data sets ensures that the comparisons are accurate and meaningful. Differences in definitions, methodologies, and coverage can lead to misleading results.
5. How do economic policies affect inequality levels?
Economic policies such as taxation, social welfare programs, and labor market regulations can significantly impact inequality levels. Progressive taxation and strong social safety nets tend to reduce inequality.
6. What are some common pitfalls to avoid when comparing inequalities?
Common pitfalls include using incompatible data sets, ignoring contextual differences, misinterpreting inequality metrics, and over-relying on a single metric.
7. How can decomposition analysis be used to understand inequality?
Decomposition analysis breaks down overall inequality into its component parts, such as income source and population group, helping to identify the factors that contribute most to inequality.
8. What role does COMPARE.EDU.VN play in facilitating inequality comparisons?
COMPARE.EDU.VN provides access to reliable data, offers tools for visualization and analysis, and promotes informed decision-making by providing users with the resources they need to compare inequalities effectively.
9. How can visualizing inequality data help in understanding inequality trends?
Visualizing inequality data through tools like Lorenz curves, histograms, and interactive data visualization platforms can reveal patterns and trends that might be missed in numerical data alone.
10. What are some future directions in inequality comparisons?
Future directions include incorporating new data sources, developing new methods for analyzing inequality data, and addressing data gaps in developing countries.
Conclusion
Comparing inequalities is a complex but essential task. By understanding the basics of inequalities, using appropriate methods, and avoiding common pitfalls, it is possible to make meaningful comparisons that can inform policy-making, investment decisions, and social and economic research. COMPARE.EDU.VN is here to help you navigate this complex landscape by providing reliable data, powerful tools, and expert analysis.
Ready to make informed decisions based on comprehensive comparisons? Visit COMPARE.EDU.VN today to explore our resources and tools. Make the smart choice with COMPARE.EDU.VN. Our team is located at 333 Comparison Plaza, Choice City, CA 90210, United States. Contact us via Whatsapp at +1 (626) 555-9090. For more information, visit our website at compare.edu.vn.
