Comparing fractions with unlike denominators can seem daunting, but it’s a fundamental skill in mathematics. COMPARE.EDU.VN is here to provide a comprehensive guide, exploring various methods to simplify and master this essential concept, ensuring clarity and precision in your comparisons. We’ll delve into finding common denominators, utilizing decimal conversions, and applying cross-multiplication, offering clear steps and examples to improve your understanding.
1. Understanding the Basics of Fractions
Before diving into comparing fractions with unlike denominators, let’s solidify our understanding of what fractions are and their components. A fraction represents a part of a whole and consists of two main parts: the numerator and the denominator. The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
- Numerator: The top number in a fraction, indicating how many parts of the whole are being considered.
- Denominator: The bottom number in a fraction, indicating the total number of equal parts the whole is divided into.
Understanding these basic components is crucial for effectively comparing fractions. Without a solid grasp of numerators and denominators, the comparison process can become confusing and lead to errors. Thus, ensuring a clear understanding of these fundamental concepts is the first step towards mastering fraction comparisons.
2. Identifying Unlike Denominators
The first step in comparing fractions is identifying whether they have the same or different denominators. Fractions with the same denominators are straightforward to compare, as you only need to compare their numerators. However, when fractions have unlike denominators, a bit more work is required.
What are Unlike Denominators?
Unlike denominators are different numbers in the bottom part of fractions. For instance, in the fractions 1/3 and 1/4, the denominators 3 and 4 are different, making them unlike denominators. These fractions cannot be directly compared until their denominators are made the same.
Why is it important to identify unlike denominators?
Identifying unlike denominators is crucial because it determines the method you will use to compare the fractions. Recognizing that the denominators are different signals that you need to find a common denominator before making a meaningful comparison. This foundational step ensures that the fractions are expressed in comparable terms.
3. The Importance of Finding a Common Denominator
Finding a common denominator is a fundamental step when comparing fractions with unlike denominators. It involves converting the fractions into equivalent forms that share the same denominator. This process allows for a direct comparison of the numerators, making it easier to determine which fraction is larger or smaller.
Why is it necessary to find a common denominator?
When fractions have different denominators, they represent parts of wholes that are divided into different numbers of pieces. Comparing them directly would be like comparing apples and oranges. Finding a common denominator essentially re-slices the wholes into the same number of pieces, allowing for a fair comparison of the number of pieces each fraction represents.
How does a common denominator help in comparing fractions?
A common denominator provides a standardized unit for comparison. Once the fractions have the same denominator, you can simply compare their numerators. The fraction with the larger numerator is the larger fraction. This method simplifies the comparison process and ensures accuracy.
4. Methods for Finding a Common Denominator
There are several methods for finding a common denominator, each with its own advantages. Here are some of the most commonly used techniques:
4.1. Listing Multiples
One straightforward method for finding a common denominator is by listing the multiples of each denominator until you find a common multiple.
- Step 1: List the multiples of each denominator. For example, to compare 1/4 and 2/6, list the multiples of 4 and 6:
- Multiples of 4: 4, 8, 12, 16, 20, 24, …
- Multiples of 6: 6, 12, 18, 24, 30, …
- Step 2: Identify the common multiples. Look for numbers that appear in both lists. In this case, 12 and 24 are common multiples of 4 and 6.
- Step 3: Choose the least common multiple (LCM). The LCM is the smallest number that is a multiple of both denominators. In this example, the LCM of 4 and 6 is 12.
Using the LCM as the common denominator makes the subsequent calculations simpler, but any common multiple will work.
4.2. Prime Factorization
Prime factorization is another effective method for finding the least common multiple (LCM) and, consequently, the common denominator.
- Step 1: Find the prime factorization of each denominator. For example, to compare 3/8 and 5/12:
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Step 2: Identify the highest power of each prime factor. In this case, the highest power of 2 is 2³ and the highest power of 3 is 3¹.
- Step 3: Multiply the highest powers together. LCM (8, 12) = 2³ x 3¹ = 8 x 3 = 24.
The LCM, 24, is the common denominator for the fractions 3/8 and 5/12.
4.3. Using the Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest multiple that two or more numbers share. Using the LCM as the common denominator simplifies the process and ensures that the resulting fractions are in their simplest form.
- Step 1: Determine the denominators of the fractions. For example, let’s compare 1/3 and 1/5. The denominators are 3 and 5.
- Step 2: Find the LCM of the denominators. The LCM of 3 and 5 is 15 because 15 is the smallest number that both 3 and 5 divide into evenly.
- Step 3: Use the LCM as the common denominator. Convert each fraction to an equivalent fraction with the LCM as the denominator.
4.4. Butterfly Method
The Butterfly Method is a visual and quick way to compare two fractions. It doesn’t directly find a common denominator, but it provides a shortcut to determine which fraction is larger.
- Step 1: Draw a butterfly shape connecting the numerators and denominators. For example, to compare 2/5 and 3/7, draw a curved line from the numerator of the first fraction (2) to the denominator of the second fraction (7), forming one wing. Then, draw another curved line from the numerator of the second fraction (3) to the denominator of the first fraction (5), forming the other wing.
- Step 2: Multiply along each wing.
- For the first wing: 2 x 7 = 14
- For the second wing: 3 x 5 = 15
- Step 3: Compare the products. The side with the larger product represents the larger fraction. In this case, 15 is greater than 14, so 3/7 is greater than 2/5.
This method is particularly useful for quick comparisons and doesn’t require finding a common denominator explicitly.
5. Converting Fractions to Equivalent Forms
Once you have identified the common denominator, the next step is to convert each fraction to an equivalent form with that denominator. This involves multiplying both the numerator and the denominator of each fraction by a factor that will result in the common denominator.
Why is this step necessary?
This step is essential because it ensures that each fraction represents the same proportion of the whole, but with a common unit of measurement. Converting fractions to equivalent forms allows for a direct and accurate comparison of their values.
How to convert fractions to equivalent forms:
- Step 1: Determine the factor needed for each fraction. To do this, divide the common denominator by the original denominator of each fraction.
- Step 2: Multiply both the numerator and the denominator of each fraction by its respective factor. This will result in equivalent fractions that share the common denominator.
For example, let’s convert 1/3 and 1/5 to equivalent fractions with a common denominator of 15:
- For 1/3: 15 ÷ 3 = 5. Multiply both the numerator and the denominator by 5: (1 x 5) / (3 x 5) = 5/15
- For 1/5: 15 ÷ 5 = 3. Multiply both the numerator and the denominator by 3: (1 x 3) / (5 x 3) = 3/15
Now, the fractions 1/3 and 1/5 have been converted to their equivalent forms, 5/15 and 3/15, respectively, with a common denominator of 15.
6. Comparing Numerators
With the fractions now having a common denominator, the next step is to compare their numerators. This is a straightforward process: simply look at the numerators of the equivalent fractions and determine which is larger or smaller.
How to compare the numerators:
- Step 1: Identify the numerators of the equivalent fractions. These are the numbers on the top of each fraction after they have been converted to have a common denominator.
- Step 2: Compare the numerators. Determine which numerator is larger, smaller, or if they are equal.
For example, after converting 1/3 and 1/5 to equivalent fractions with a common denominator of 15, we have 5/15 and 3/15. The numerators are 5 and 3. Since 5 is greater than 3, we can conclude that 5/15 is greater than 3/15.
What does the comparison of numerators tell us?
The comparison of numerators directly indicates the relative size of the fractions. The fraction with the larger numerator is the larger fraction, as it represents more parts of the whole when the whole is divided into the same number of parts (the common denominator).
7. Determining the Larger or Smaller Fraction
After comparing the numerators, determining the larger or smaller fraction is straightforward. The fraction with the larger numerator is the larger fraction, and the fraction with the smaller numerator is the smaller fraction.
How to determine the larger or smaller fraction:
- Step 1: Recall the numerators of the equivalent fractions. These are the numbers on top of each fraction after conversion to a common denominator.
- Step 2: Compare the numerators. Identify which numerator is larger or smaller.
- Step 3: Conclude which fraction is larger or smaller. The fraction with the larger numerator is the larger fraction, and the fraction with the smaller numerator is the smaller fraction.
For example, after converting 1/3 and 1/5 to equivalent fractions with a common denominator of 15, we have 5/15 and 3/15. Since 5 is greater than 3, we conclude that 5/15 is greater than 3/15, and therefore, 1/3 is greater than 1/5.
8. Decimal Method for Comparing Fractions
Another effective method for comparing fractions, especially those with unlike denominators, is to convert them into decimal form. This approach simplifies the comparison process by expressing each fraction as a decimal number, allowing for a direct comparison using decimal values.
How to convert fractions to decimals:
- Step 1: Divide the numerator by the denominator. Perform the division for each fraction to convert it into its decimal equivalent.
- Step 2: Compare the decimal values. Once the fractions are in decimal form, compare their values to determine which is larger or smaller.
For example, let’s compare 3/8 and 5/12 using the decimal method:
- Convert 3/8 to a decimal: 3 ÷ 8 = 0.375
- Convert 5/12 to a decimal: 5 ÷ 12 = 0.4166… (approximately 0.417)
Comparing the decimal values, we see that 0.417 is greater than 0.375. Therefore, 5/12 is greater than 3/8.
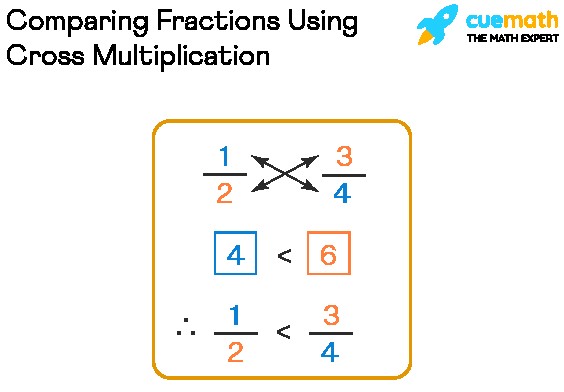
9. Cross Multiplication Method for Comparing Fractions
Cross multiplication is a quick and efficient method for comparing two fractions, especially when you need a fast comparison without finding a common denominator. This method involves multiplying the numerator of one fraction by the denominator of the other fraction and comparing the results.
How to use cross multiplication:
- Step 1: Write down the two fractions you want to compare. For example, let’s compare 2/5 and 3/7.
- Step 2: Cross multiply. Multiply the numerator of the first fraction by the denominator of the second fraction, and multiply the numerator of the second fraction by the denominator of the first fraction.
- 2 x 7 = 14
- 3 x 5 = 15
- Step 3: Compare the results. The fraction that corresponds to the larger product is the larger fraction.
- Since 15 is greater than 14, 3/7 is greater than 2/5.
This method provides a straightforward way to determine which fraction is larger or smaller without explicitly finding a common denominator.
10. Visual Aids for Comparing Fractions
Visual aids are powerful tools for understanding and comparing fractions, especially for those who learn best through visual representations. Using diagrams, charts, and models can make the abstract concept of fractions more concrete and easier to grasp.
Types of Visual Aids:
- Fraction Bars: Fraction bars are rectangular bars divided into equal parts, with each part representing a fraction of the whole. By comparing the shaded portions of different fraction bars, you can easily see which fraction is larger or smaller.
- Circle Diagrams: Circle diagrams, also known as pie charts, divide a circle into equal sectors, with each sector representing a fraction of the whole. Comparing the sizes of the sectors helps visualize the relative sizes of the fractions.
- Number Lines: Number lines provide a linear representation of fractions, allowing you to compare their positions and determine which fraction is larger or smaller.
How to use visual aids:
- Step 1: Represent each fraction visually. Use fraction bars, circle diagrams, or number lines to represent each fraction you want to compare.
- Step 2: Compare the visual representations. Observe the diagrams or models to determine which fraction represents a larger or smaller portion of the whole.
For example, if you want to compare 1/4 and 1/2 using fraction bars, you would create two bars of equal length, one divided into four equal parts and the other into two equal parts. Shading one part of each bar, you can visually see that 1/2 covers a larger portion of the bar than 1/4, indicating that 1/2 is greater than 1/4.
11. Real-World Applications of Comparing Fractions
Comparing fractions isn’t just a theoretical exercise; it has numerous practical applications in everyday life. From cooking and baking to finance and construction, the ability to compare fractions is essential for making informed decisions and solving problems.
Examples of Real-World Applications:
- Cooking and Baking: Recipes often involve fractions of ingredients. Comparing fractions helps you adjust recipes, scale them up or down, and ensure the correct proportions of ingredients.
- Finance: In personal finance, comparing fractions is useful for understanding discounts, calculating interest rates, and determining the best deals.
- Construction: In construction and carpentry, fractions are used for measuring lengths, calculating areas, and ensuring precise cuts.
- Time Management: When planning your day, you might allocate fractional amounts of time to different tasks. Comparing these fractions helps you prioritize and manage your schedule effectively.
12. Common Mistakes to Avoid When Comparing Fractions
When comparing fractions, especially those with unlike denominators, it’s easy to make mistakes if you’re not careful. Here are some common errors to avoid:
Common Mistakes:
- Comparing numerators directly without a common denominator: This is a fundamental mistake that leads to incorrect comparisons. You must find a common denominator before comparing numerators.
- Incorrectly finding the least common multiple (LCM): An incorrect LCM will result in inaccurate equivalent fractions and lead to wrong comparisons.
- Forgetting to multiply both the numerator and denominator: When converting fractions to equivalent forms, it’s crucial to multiply both the numerator and denominator by the same factor. Failing to do so changes the value of the fraction.
- Making arithmetic errors: Simple arithmetic mistakes can lead to incorrect calculations and wrong comparisons.
How to Avoid These Mistakes:
- Always find a common denominator before comparing numerators.
- Double-check your LCM calculations.
- Ensure you multiply both the numerator and denominator by the same factor when converting fractions.
- Take your time and double-check your arithmetic.
13. Practice Problems and Solutions
To solidify your understanding of comparing fractions with unlike denominators, here are some practice problems with detailed solutions:
Problem 1: Compare 2/5 and 3/8.
- Solution:
- Find the LCM of 5 and 8: LCM (5, 8) = 40
- Convert 2/5 to an equivalent fraction: (2 x 8) / (5 x 8) = 16/40
- Convert 3/8 to an equivalent fraction: (3 x 5) / (8 x 5) = 15/40
- Compare the numerators: 16 > 15
- Therefore, 2/5 > 3/8
Problem 2: Compare 1/4 and 2/7.
- Solution:
- Find the LCM of 4 and 7: LCM (4, 7) = 28
- Convert 1/4 to an equivalent fraction: (1 x 7) / (4 x 7) = 7/28
- Convert 2/7 to an equivalent fraction: (2 x 4) / (7 x 4) = 8/28
- Compare the numerators: 8 > 7
- Therefore, 2/7 > 1/4
Problem 3: Compare 4/9 and 5/11.
- Solution:
- Find the LCM of 9 and 11: LCM (9, 11) = 99
- Convert 4/9 to an equivalent fraction: (4 x 11) / (9 x 11) = 44/99
- Convert 5/11 to an equivalent fraction: (5 x 9) / (11 x 9) = 45/99
- Compare the numerators: 45 > 44
- Therefore, 5/11 > 4/9
14. Advanced Techniques and Strategies
For those looking to deepen their understanding of comparing fractions, here are some advanced techniques and strategies that can be helpful:
- Benchmarking: Compare each fraction to a common benchmark, such as 1/2 or 1. This can help quickly determine the relative size of the fractions without finding a common denominator.
- Estimating: Estimate the value of each fraction and compare the estimates. This can be useful for quickly approximating which fraction is larger or smaller.
- Using Properties of Fractions: Understand and apply properties such as the fact that if two fractions have the same numerator, the fraction with the smaller denominator is larger.
15. Frequently Asked Questions (FAQs)
Q1: What does comparing fractions mean?
Comparing fractions means determining which fraction is larger, smaller, or if they are equal in value. This is essential for various mathematical operations and real-world applications.
Q2: Why is it important to find a common denominator when comparing fractions?
Finding a common denominator ensures that the fractions are expressed in terms of the same unit, allowing for a direct and accurate comparison of their values.
Q3: What is the easiest way to compare fractions with unlike denominators?
One of the easiest ways is to convert the fractions to decimals and then compare the decimal values. Alternatively, you can use cross multiplication for a quick comparison.
Q4: What is the butterfly method for comparing fractions?
The butterfly method involves cross multiplying the numerator of one fraction by the denominator of the other fraction, and then comparing the results to determine which fraction is larger.
Q5: How can visual aids help in comparing fractions?
Visual aids such as fraction bars, circle diagrams, and number lines provide a visual representation of fractions, making it easier to compare their relative sizes.
Q6: What is the least common multiple (LCM) and how is it used in comparing fractions?
The least common multiple (LCM) is the smallest multiple that two or more numbers share. It is used as the common denominator when converting fractions to equivalent forms for comparison.
Q7: What are some common mistakes to avoid when comparing fractions?
Common mistakes include comparing numerators directly without a common denominator, incorrectly finding the LCM, and forgetting to multiply both the numerator and denominator when converting fractions.
Q8: How can I improve my skills in comparing fractions?
Practice regularly, use visual aids, and apply different methods to compare fractions. Understanding the underlying concepts and avoiding common mistakes will also help improve your skills.
Q9: Can I always use the decimal method to compare fractions?
Yes, you can always use the decimal method to compare fractions. It provides a straightforward and accurate way to compare the values of fractions by converting them to decimal form.
Q10: Is there a shortcut to comparing fractions without finding a common denominator?
Yes, the butterfly method and benchmarking are shortcuts that allow you to compare fractions without explicitly finding a common denominator.
16. Conclusion: Mastering Fraction Comparisons
Comparing fractions with unlike denominators is a crucial skill with numerous practical applications. By understanding the fundamental concepts, mastering the various methods, and avoiding common mistakes, you can confidently compare fractions and solve related problems. Whether you prefer finding a common denominator, converting to decimals, or using visual aids, the key is to practice regularly and apply the techniques that work best for you.
Ready to put your fraction comparison skills to the test? Visit COMPARE.EDU.VN today to explore more resources, practice problems, and in-depth guides that will help you master this essential mathematical concept. Whether you are a student, a professional, or simply someone looking to brush up on your math skills, COMPARE.EDU.VN provides the tools and support you need to succeed. Don’t wait—start your journey to mathematical mastery with us today!
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
WhatsApp: +1 (626) 555-9090
Website: compare.edu.vn