Comparing fractions with like denominators is a fundamental skill in mathematics, crucial for various real-life applications. This guide, brought to you by COMPARE.EDU.VN, simplifies the process of fraction comparison, enabling you to effortlessly determine which fraction is larger or smaller when they share a common denominator. Understand fraction magnitude, equivalent fractions and apply this knowledge to solve problems accurately.
1. Understanding the Basics of Fractions
Before diving into the comparison methods, let’s ensure we have a firm grasp on what fractions are and their components.
1.1. Defining a Fraction
A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The number above the fraction bar, indicating how many parts of the whole we have.
- Denominator: The number below the fraction bar, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator, and 4 is the denominator. It signifies that we have 3 parts out of a total of 4.
1.2. Types of Fractions
Understanding the different types of fractions is essential for comparison and other mathematical operations. Here are the main types:
- Proper Fractions: The numerator is less than the denominator (e.g., 2/5).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 7/3).
- Mixed Numbers: A whole number combined with a proper fraction (e.g., 1 1/2).
- Equivalent Fractions: Fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 and 2/4).
2. Comparing Fractions with Like Denominators: The Simple Rule
When fractions share the same denominator, the comparison becomes straightforward. The rule is simple: the fraction with the larger numerator is the larger fraction.
2.1. The Core Principle
If two fractions have the same denominator, they are dividing the whole into the same number of equal parts. Therefore, the fraction with more of those parts is the larger one.
2.2. Step-by-Step Comparison
Here’s How To Compare Fractions With Like Denominators:
- Identify the Denominators: Ensure that the denominators of the fractions you want to compare are the same.
- Compare the Numerators: Look at the numerators of the fractions.
- Determine the Larger Fraction: The fraction with the larger numerator is the larger fraction.
2.3. Example 1: Comparing 3/8 and 5/8
Both fractions have a denominator of 8, meaning the whole is divided into 8 equal parts. Since 5 is greater than 3, the fraction 5/8 is larger than 3/8.
Therefore, 5/8 > 3/8.
2.4. Example 2: Comparing 7/10 and 2/10
Both fractions have a denominator of 10. Comparing the numerators, 7 is greater than 2. Thus, 7/10 is larger than 2/10.
Therefore, 7/10 > 2/10.
3. Visual Aids for Comparing Fractions
Visual aids can make the concept of comparing fractions more intuitive, especially for learners who benefit from visual representation.
3.1. Using Fraction Bars
Fraction bars are rectangular bars divided into equal parts to represent fractions. To compare fractions with like denominators, you can use fraction bars to visually represent each fraction and compare the shaded areas.
3.1.1. Example: Comparing 1/4 and 3/4 with Fraction Bars
Draw two identical bars. Divide each into four equal parts. Shade one part of the first bar to represent 1/4, and shade three parts of the second bar to represent 3/4. Visually, you can see that 3/4 covers a larger area than 1/4.
3.2. Using Pie Charts
Pie charts (or circles) can also be used to represent fractions. Divide a circle into equal sectors, with each sector representing a fraction of the whole.
3.2.1. Example: Comparing 2/6 and 5/6 with Pie Charts
Draw two identical circles. Divide each into six equal sectors. Shade two sectors of the first circle to represent 2/6, and shade five sectors of the second circle to represent 5/6. The pie chart representing 5/6 will have a larger shaded area, illustrating that 5/6 is greater than 2/6.
4. Real-World Applications of Comparing Fractions
Understanding how to compare fractions is not just a mathematical exercise; it has practical applications in everyday life.
4.1. Cooking and Baking
In cooking, recipes often require you to measure ingredients in fractions. Knowing how to compare fractions helps you adjust recipes and understand proportions.
4.1.1. Example: Adjusting a Recipe
Suppose a recipe calls for 1/3 cup of flour and 2/3 cup of sugar. Comparing these fractions allows you to understand that you need twice as much sugar as flour.
4.2. Measuring and Construction
In construction and DIY projects, measurements are often in fractions. Comparing these fractions ensures accuracy.
4.2.1. Example: Cutting Wood
If you need to cut a piece of wood to be 3/8 inch thick and another to be 5/8 inch thick, knowing that 5/8 is greater than 3/8 helps you identify which piece should be thicker.
4.3. Time Management
Fractions can represent portions of time. Comparing these fractions helps you manage your schedule effectively.
4.3.1. Example: Allocating Time
If you spend 1/4 of your day working and 3/4 of your day on other activities, comparing these fractions shows that you spend more time on non-work activities.
5. Comparing More Than Two Fractions
The same principles apply when comparing more than two fractions with like denominators. Arrange the fractions in ascending or descending order based on their numerators.
5.1. Ascending Order
Arrange the fractions from smallest to largest.
5.1.1. Example: Ordering 1/5, 3/5, and 2/5
All fractions have the same denominator of 5. Comparing the numerators, we have 1 < 2 < 3. Therefore, the fractions in ascending order are 1/5, 2/5, and 3/5.
5.2. Descending Order
Arrange the fractions from largest to smallest.
5.2.1. Example: Ordering 4/7, 2/7, and 6/7
All fractions have the same denominator of 7. Comparing the numerators, we have 6 > 4 > 2. Therefore, the fractions in descending order are 6/7, 4/7, and 2/7.
6. Common Mistakes to Avoid
While comparing fractions with like denominators is straightforward, it’s essential to avoid common mistakes that can lead to incorrect comparisons.
6.1. Ignoring the Denominator
Always ensure that the denominators are the same before comparing numerators. If the denominators are different, you cannot directly compare the numerators.
6.2. Misinterpreting the Numerator
The numerator represents the number of parts you have, not the size of the parts. If the denominators are the same, a larger numerator means you have more parts of the same size, hence a larger fraction.
6.3. Not Simplifying Fractions
Sometimes, fractions can be simplified. Simplifying fractions before comparing them can make the comparison easier.
6.3.1. Example: Comparing 4/8 and 1/2
4/8 can be simplified to 1/2. Therefore, 4/8 and 1/2 are equal.
7. Advanced Concepts: Equivalent Fractions
Understanding equivalent fractions can help simplify the comparison process, especially when dealing with fractions that can be reduced or scaled.
7.1. What are Equivalent Fractions?
Equivalent fractions are fractions that represent the same value but have different numerators and denominators. For example, 1/2, 2/4, and 3/6 are equivalent fractions.
7.2. Finding Equivalent Fractions
To find equivalent fractions, multiply or divide both the numerator and the denominator by the same non-zero number.
7.2.1. Example: Finding Equivalent Fractions of 2/3
- Multiply by 2: (2/3) * (2/2) = 4/6
- Multiply by 3: (2/3) * (3/3) = 6/9
Therefore, 4/6 and 6/9 are equivalent to 2/3.
7.3. Using Equivalent Fractions for Comparison
When comparing fractions with unlike denominators, finding equivalent fractions with a common denominator is a crucial step.
8. Practical Exercises for Mastering Fraction Comparison
Practice is key to mastering any mathematical concept. Here are some exercises to help you solidify your understanding of comparing fractions with like denominators.
8.1. Exercise 1: Basic Comparison
Compare the following pairs of fractions:
- 2/7 and 5/7
- 1/9 and 4/9
- 3/11 and 8/11
- 6/13 and 5/13
- 9/15 and 7/15
8.2. Exercise 2: Ordering Fractions
Arrange the following sets of fractions in ascending order:
- 1/6, 4/6, 2/6
- 3/8, 1/8, 5/8
- 2/9, 7/9, 4/9
8.3. Exercise 3: Real-World Problems
- John ate 2/5 of a pizza, and Mary ate 3/5 of the same pizza. Who ate more?
- Sarah ran 1/4 of a mile, and Tom ran 3/4 of a mile. Who ran farther?
- A recipe calls for 2/7 cup of sugar and 4/7 cup of flour. Which ingredient is needed more?
9. How COMPARE.EDU.VN Can Help You Further
COMPARE.EDU.VN offers a comprehensive suite of tools and resources to deepen your understanding of fractions and other mathematical concepts.
9.1. Detailed Comparison Guides
Access in-depth guides that break down complex topics into easy-to-understand steps.
9.2. Interactive Tools
Use our interactive tools to practice comparing fractions and test your knowledge.
9.3. Expert Insights
Benefit from expert insights and tips to improve your understanding and problem-solving skills.
9.4. Real-World Examples
Explore real-world examples that demonstrate how fractions are used in various scenarios.
10. Conclusion: Mastering Fraction Comparison
Comparing fractions with like denominators is a foundational skill that opens the door to more complex mathematical concepts. By understanding the basic principles, using visual aids, and practicing regularly, you can master this skill and apply it in various real-world situations. Rely on COMPARE.EDU.VN for comprehensive guides, interactive tools, and expert insights to enhance your learning experience.
11. Call to Action
Ready to take your understanding of fractions to the next level? Visit COMPARE.EDU.VN today to explore our resources and tools. Whether you’re a student, a professional, or simply someone looking to improve your math skills, we have something for everyone. Don’t let fractions intimidate you; empower yourself with the knowledge and confidence you need to succeed.
Take the next step and visit COMPARE.EDU.VN now!
12. FAQs About Comparing Fractions
12.1. What does it mean to compare fractions?
Comparing fractions means determining which fraction is larger or smaller in value. This is a fundamental skill in mathematics that helps in various real-life scenarios, such as cooking, measuring, and time management.
12.2. What is the rule for comparing fractions with the same denominator?
When fractions have the same denominator, the fraction with the larger numerator is the larger fraction. The denominator represents the total number of equal parts, and the numerator represents how many of those parts you have.
12.3. How do you compare fractions with different denominators?
To compare fractions with different denominators, you first need to find a common denominator. This is usually the least common multiple (LCM) of the denominators. Once you have a common denominator, you can compare the numerators as you would with fractions that have the same denominator.
12.4. What are equivalent fractions?
Equivalent fractions are fractions that represent the same value but have different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions because they both represent half of a whole.
12.5. Why is comparing fractions important?
Comparing fractions is important because it helps us understand the relative sizes of different quantities. This skill is used in many areas of life, from cooking and baking to construction and finance.
12.6. Can you use decimals to compare fractions?
Yes, you can convert fractions to decimals and then compare the decimal values. This method is particularly useful when the fractions have different denominators and finding a common denominator is difficult.
12.7. How can visual aids help in comparing fractions?
Visual aids like fraction bars and pie charts can make the concept of comparing fractions more intuitive. These tools provide a visual representation of the fractions, making it easier to see which one is larger.
12.8. What is the biggest mistake people make when comparing fractions?
The biggest mistake is ignoring the denominator and directly comparing the numerators when the denominators are different. Always ensure the denominators are the same before comparing the numerators.
12.9. Are there any shortcuts for comparing fractions?
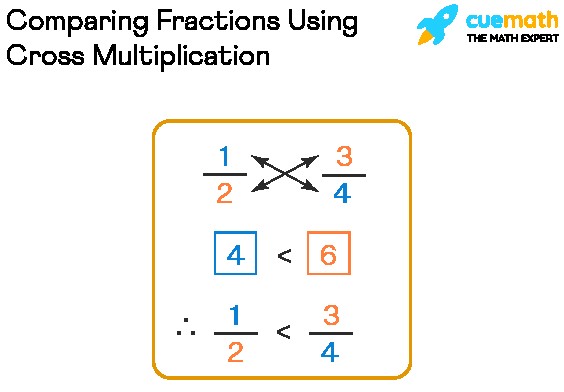
One shortcut is to cross-multiply the fractions. If you have two fractions, a/b and c/d, multiply a by d and b by c. Compare the products: if ad > bc, then a/b > c/d; if ad < bc, then a/b < c/d; and if ad = bc, then a/b = c/d.
12.10. How can I practice comparing fractions?
You can practice by working through exercises, using online tools and resources, and applying the concept in real-life situations. Regularly practicing will help you build confidence and master the skill.
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
Whatsapp: +1 (626) 555-9090
Website: compare.edu.vn