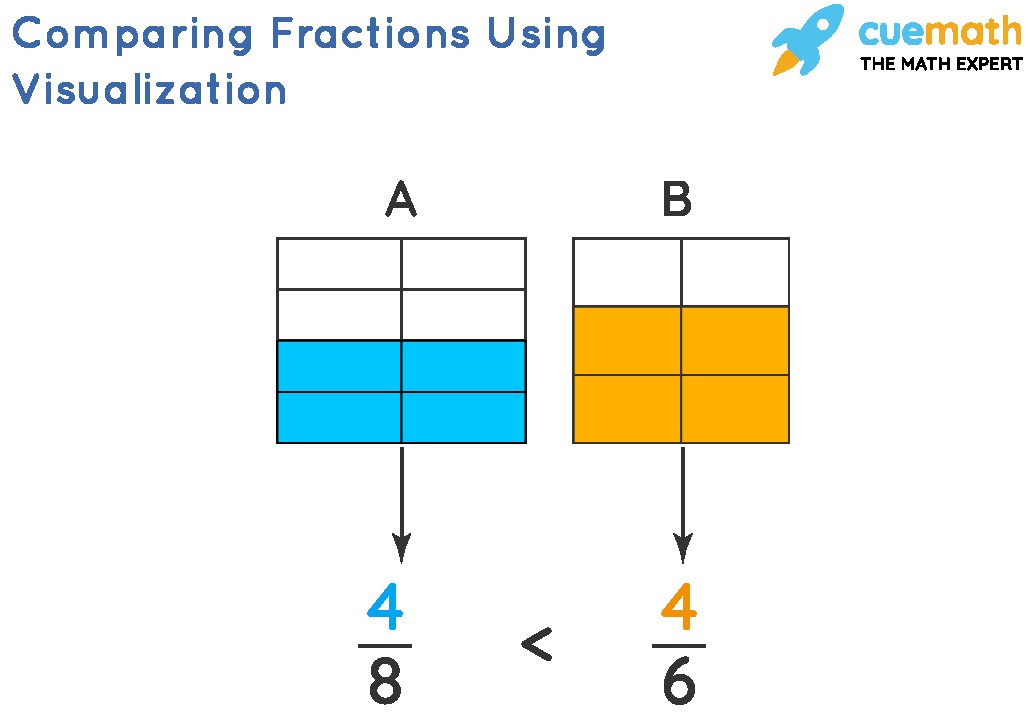
Comparing fractions involves determining which fraction is larger or smaller. This guide provides a step-by-step approach to comparing fractions, regardless of whether they have the same or different denominators.
Comparing Fractions with the Same Denominator
When two fractions share the same denominator, comparing them is straightforward. Simply compare the numerators:
- Identify the denominators: Ensure both fractions have identical denominators.
- Compare the numerators: The fraction with the larger numerator is the larger fraction. If the numerators are equal, the fractions are equal.
Example: Compare 3/5 and 2/5. Both have a denominator of 5. Since 3 > 2, then 3/5 > 2/5.
Comparing Fractions with Different Denominators
Comparing fractions with unlike denominators requires finding a common denominator:
- Find the Least Common Multiple (LCM): Determine the LCM of the two denominators. This will be the new common denominator.
- Create Equivalent Fractions: Multiply each fraction by a value (numerator and denominator) that results in the LCM as the new denominator.
- Compare the Numerators: Now that the denominators are the same, compare the numerators as described in the previous section.
Example: Compare 1/2 and 2/3.
- The LCM of 2 and 3 is 6.
- Multiply 1/2 by 3/3: (1 x 3) / (2 x 3) = 3/6
- Multiply 2/3 by 2/2: (2 x 2) / (3 x 2) = 4/6
- Since 4 > 3, then 4/6 > 3/6, and therefore, 2/3 > 1/2.
Using Decimal Equivalents for Comparison
Another method involves converting fractions to decimals:
- Divide the numerator by the denominator: For each fraction, perform the division to obtain its decimal equivalent.
- Compare the decimals: Compare the resulting decimal values. The larger decimal represents the larger fraction.
Example: Compare 3/4 and 5/8.
- 3/4 = 0.75
- 5/8 = 0.625
- Since 0.75 > 0.625, then 3/4 > 5/8.
Cross-Multiplication Method
Cross-multiplication offers a quick way to compare fractions:
- Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction. Write the product above the first fraction.
- Multiply: Multiply the numerator of the second fraction by the denominator of the first fraction. Write the product above the second fraction.
- Compare the Products: The larger product indicates the larger fraction.
Example: Compare 2/5 and 3/7.
- 2 x 7 = 14 (above 2/5)
- 3 x 5 = 15 (above 3/7)
- Since 15 > 14, then 3/7 > 2/5.
Conclusion
Comparing fractions is a fundamental math skill. By understanding these step-by-step methods – finding common denominators, converting to decimals, or using cross-multiplication – you can confidently compare any two fractions. Choose the method that works best for you and practice regularly to master this essential skill.