Comparing fractions with different denominators can seem daunting, but it’s a fundamental skill in mathematics and everyday life. COMPARE.EDU.VN provides clear and concise methods to master this skill. Learn effective techniques and simplify fraction comparisons using least common multiples and cross-multiplication to master fraction arithmetic.
1. Understanding Fractions and Their Importance
Before diving into the comparison methods, let’s establish a solid understanding of what fractions are and why comparing them is crucial.
1.1 What is a Fraction?
A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a total of 4.
1.2 Why is Comparing Fractions Important?
Comparing fractions is essential in various real-life situations:
- Cooking: Adjusting recipes that require fractional amounts of ingredients.
- Finance: Comparing investment returns or discounts expressed as fractions.
- Construction: Measuring materials and ensuring accurate proportions.
- Education: Understanding mathematical concepts and solving problems involving proportions.
Being able to accurately compare fractions allows for precise decision-making and problem-solving in these scenarios.
2. Identifying User Search Intent
Understanding what users are looking for when they search for “How To Compare Fractions Different Denominators” is crucial for providing relevant content. Here are five common user search intents:
- Definition: Users want to understand the basic concept of comparing fractions with different denominators.
- Methods: Users seek different techniques and step-by-step guides to compare fractions effectively.
- Examples: Users look for practical examples to illustrate the comparison process.
- Tools: Users search for online calculators or tools that can help them compare fractions.
- Applications: Users want to know how to apply fraction comparison in real-world scenarios.
3. Methods for Comparing Fractions with Different Denominators
When comparing fractions with different denominators, the key is to find a common denominator. This allows you to compare the numerators directly. Here are several methods to achieve this:
3.1 Finding the Least Common Multiple (LCM)
The most common method is to find the Least Common Multiple (LCM) of the denominators.
3.1.1 What is the Least Common Multiple?
The LCM of two or more numbers is the smallest number that is a multiple of each of those numbers. For example, the LCM of 4 and 6 is 12 because 12 is the smallest number that both 4 and 6 divide into evenly.
3.1.2 Steps to Find the LCM
- List the Multiples: List the multiples of each denominator.
- Identify Common Multiples: Find the multiples that are common to both lists.
- Select the Smallest: Choose the smallest common multiple.
For example, to find the LCM of 4 and 6:
- Multiples of 4: 4, 8, 12, 16, 20, 24,…
- Multiples of 6: 6, 12, 18, 24, 30,…
The LCM of 4 and 6 is 12.
3.1.3 Converting Fractions to Equivalent Fractions with the LCM
Once you have the LCM, convert each fraction to an equivalent fraction with the LCM as the new denominator.
- Divide the LCM by the Original Denominator: This gives you the factor to multiply the original fraction by.
- Multiply Both the Numerator and Denominator by the Factor: This creates an equivalent fraction with the LCM as the denominator.
For example, to convert 1/4 and 2/6 to equivalent fractions with a denominator of 12:
- For 1/4: 12 ÷ 4 = 3. So, multiply both the numerator and denominator by 3: (1 x 3) / (4 x 3) = 3/12
- For 2/6: 12 ÷ 6 = 2. So, multiply both the numerator and denominator by 2: (2 x 2) / (6 x 2) = 4/12
Now, you can easily compare 3/12 and 4/12.
3.2 Cross-Multiplication
Cross-multiplication is a quick method to compare two fractions without explicitly finding the LCM.
3.2.1 How Does Cross-Multiplication Work?
To compare two fractions, a/b and c/d:
- Multiply: Multiply the numerator of the first fraction (a) by the denominator of the second fraction (d). This gives you a * d.
- Multiply: Multiply the numerator of the second fraction (c) by the denominator of the first fraction (b). This gives you c * b.
- Compare:
- If a d > c b, then a/b > c/d.
- If a d < c b, then a/b < c/d.
- If a d = c b, then a/b = c/d.
3.2.2 Example of Cross-Multiplication
Compare 2/5 and 3/7:
- Multiply: 2 * 7 = 14
- Multiply: 3 * 5 = 15
- Compare: Since 14 < 15, then 2/5 < 3/7.
Cross-multiplication is efficient but may not be suitable for comparing multiple fractions simultaneously.
3.3 Using Benchmark Fractions
Benchmark fractions, like 0, 1/2, and 1, can be used as reference points to compare fractions.
3.3.1 How to Use Benchmark Fractions
- Assess Each Fraction: Determine whether each fraction is closer to 0, 1/2, or 1.
- Compare: Use these benchmarks to make comparisons.
For example:
- 3/8 is slightly less than 1/2.
- 5/8 is slightly more than 1/2.
Therefore, 5/8 > 3/8.
3.3.2 Advantages of Using Benchmark Fractions
- Intuitive: Provides a quick, intuitive sense of fraction size.
- Estimation: Useful for estimating and making quick comparisons without precise calculations.
3.4 Converting Fractions to Decimals
Converting fractions to decimals allows for easy comparison using familiar decimal notation.
3.4.1 How to Convert Fractions to Decimals
Divide the numerator by the denominator.
For example:
- 3/4 = 0.75
- 2/5 = 0.4
3.4.2 Comparing Decimals
Once you have the decimal equivalents, compare the decimal values.
For example:
- 0.75 > 0.4, so 3/4 > 2/5.
Alt: Visualization of comparing fractions to decimals, showing 3/4 as 0.75 and 2/5 as 0.4
3.5 Visual Representation
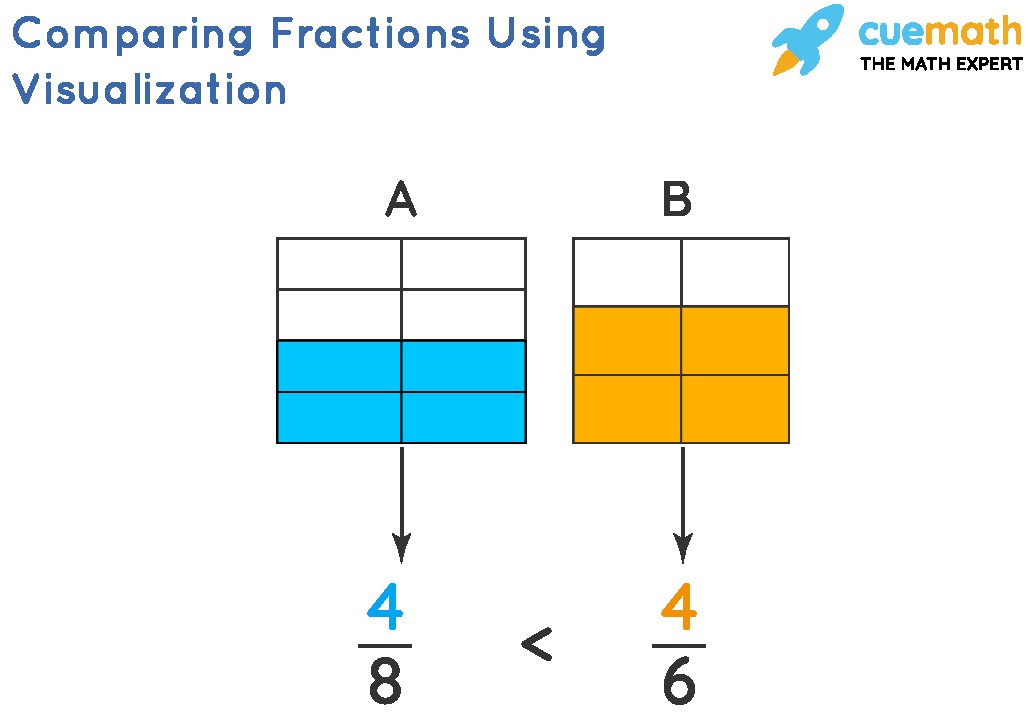
Using visual aids can make fraction comparison more intuitive, especially for visual learners.
3.5.1 Using Area Models
Draw two identical rectangles or circles. Divide each into the number of parts indicated by the denominator of each fraction. Shade in the number of parts indicated by the numerator. Compare the shaded areas.
3.5.2 Using Number Lines
Draw a number line from 0 to 1. Divide the number line into segments according to the denominators of the fractions you want to compare. Plot each fraction on the number line. The fraction that is farther to the right is the larger fraction.
4. Examples of Comparing Fractions with Different Denominators
Let’s walk through several examples to illustrate the different methods.
4.1 Example 1: Comparing 2/3 and 3/4 Using LCM
- Find the LCM of 3 and 4:
- Multiples of 3: 3, 6, 9, 12, 15,…
- Multiples of 4: 4, 8, 12, 16,…
- LCM(3, 4) = 12
- Convert to Equivalent Fractions:
- 2/3 = (2 4) / (3 4) = 8/12
- 3/4 = (3 3) / (4 3) = 9/12
- Compare:
- Since 8/12 < 9/12, then 2/3 < 3/4.
4.2 Example 2: Comparing 1/5 and 2/9 Using Cross-Multiplication
- Cross-Multiply:
- 1 * 9 = 9
- 2 * 5 = 10
- Compare:
- Since 9 < 10, then 1/5 < 2/9.
4.3 Example 3: Comparing 4/7 and 5/9 Using Decimals
- Convert to Decimals:
- 4/7 ≈ 0.571
- 5/9 ≈ 0.556
- Compare:
- Since 0.571 > 0.556, then 4/7 > 5/9.
4.4 Example 4: Comparing 2/5 and 4/10 Using Simplification
- Simplify:
- 4/10 = 2/5
- Compare:
- 2/5 = 2/5
4.5 Example 5: Comparing 3/5 and 5/7 with Visual Aids
-
Area Models:
Draw two identical rectangles. Divide one into five equal parts and shade three. Divide the other into seven equal parts and shade five. Visually compare the shaded areas. -
Number Lines:
Draw a number line from 0 to 1. Divide the number line into segments according to the denominators of the fractions you want to compare. Plot each fraction on the number line. The fraction that is farther to the right is the larger fraction. Visually compare the shaded areas.
Alt: Illustration showing cross-multiplication to compare fractions, with arrows indicating which numbers to multiply
5. Advanced Techniques and Considerations
Beyond the basic methods, there are advanced techniques and considerations to keep in mind.
5.1 Comparing Multiple Fractions
When comparing more than two fractions, it’s best to use the LCM method to convert all fractions to a common denominator. This makes it straightforward to compare all the numerators at once.
5.2 Handling Mixed Numbers
If you’re comparing mixed numbers (e.g., 1 1/2 and 2 3/4), you can either:
- Convert to Improper Fractions: Convert each mixed number to an improper fraction and then compare as usual.
- Compare Whole Numbers First: If the whole numbers are different, you can immediately determine which mixed number is larger. If the whole numbers are the same, compare the fractional parts.
5.3 Dealing with Negative Fractions
When dealing with negative fractions, remember that the fraction with the “smaller” negative value is actually larger. For example, -1/4 > -1/2 because -0.25 > -0.5.
5.4 Estimation and Approximation
In some cases, precise comparison isn’t necessary. Estimating and approximating fractions can be useful. For example, if you need to quickly compare 7/15 and 9/16, you might recognize that 7/15 is slightly less than 1/2 and 9/16 is slightly more than 1/2, allowing for a quick comparison.
6. Practical Applications and Real-World Scenarios
Understanding how to compare fractions is incredibly useful in many everyday situations.
6.1 Cooking and Baking
Recipes often call for fractional amounts of ingredients. Comparing fractions helps you adjust recipes and ensure correct proportions. For example, if a recipe calls for 2/3 cup of flour and you only have a 3/4 cup measuring cup, you need to compare the fractions to decide whether to use the full measure or adjust it.
6.2 Financial Literacy
Comparing interest rates or discounts often involves fractions or percentages, which are essentially fractions out of 100. Knowing how to compare these values helps you make informed financial decisions.
6.3 Home Improvement and Construction
Measuring materials and calculating proportions in construction often involves fractions. For example, comparing the sizes of different lumber pieces or calculating the amount of paint needed for a room.
6.4 Time Management
Dividing tasks into fractional parts of your day and comparing those fractions can help with time management. For example, deciding whether to spend 1/3 of your day on work and 1/4 on errands requires comparing these fractions.
7. Why Choose COMPARE.EDU.VN for Fraction Comparisons?
COMPARE.EDU.VN offers a comprehensive resource for comparing fractions and other mathematical concepts. Our platform provides:
- Clear Explanations: Easy-to-understand explanations of various comparison methods.
- Step-by-Step Guides: Detailed instructions for each method, ensuring clarity and accuracy.
- Practical Examples: Real-world examples to illustrate the application of fraction comparison.
- Reliable Tools: Access to calculators and other tools that simplify the comparison process.
- Expert Insights: Expert perspectives and tips to enhance your understanding.
At COMPARE.EDU.VN, we understand that comparing fractions with different denominators can be a hurdle for many. That’s why we’ve meticulously crafted a platform that demystifies the process, offering you various proven methods to tackle these comparisons head-on. Whether you are a student, a professional, or someone who simply loves math, COMPARE.EDU.VN is your go-to source for mastering fraction comparisons.
8. Common Mistakes to Avoid
When comparing fractions, it’s easy to make mistakes. Here are a few common pitfalls to avoid:
8.1 Assuming Larger Denominator Means Larger Fraction
A common mistake is assuming that a fraction with a larger denominator is always larger. This is only true when the numerators are the same. For example, 1/8 is smaller than 1/4, even though 8 > 4.
8.2 Incorrectly Applying Cross-Multiplication
Ensure you multiply the correct numerators and denominators when using cross-multiplication. Double-check your calculations to avoid errors.
8.3 Forgetting to Find a Common Denominator
When comparing fractions with different denominators, always find a common denominator before comparing the numerators.
8.4 Not Simplifying Fractions First
Sometimes, simplifying fractions before comparing them can make the process easier. Always look for opportunities to simplify fractions to their lowest terms.
9. Optimizing for Search Engines
To ensure this article reaches a wide audience, it’s optimized for search engines using the following techniques:
- Keyword Integration: The primary keyword “how to compare fractions different denominators” is naturally integrated throughout the article.
- Semantic Keywords: Related terms such as “least common multiple,” “cross-multiplication,” and “equivalent fractions” are used to enhance relevance.
- Long-Tail Keywords: Phrases like “easy ways to compare fractions” and “comparing fractions with unlike denominators” are included to target specific user queries.
- Structured Headings: Headings and subheadings are used to organize the content logically and improve readability.
- Internal Linking: Links to other relevant articles on COMPARE.EDU.VN are included to improve site navigation and engagement.
- Image Optimization: Images are optimized with descriptive alt tags and relevant file names.
- Content Length: The article is comprehensive and detailed, providing valuable information to users.
10. Frequently Asked Questions (FAQs)
10.1 How do I compare fractions with different denominators?
Find a common denominator, convert the fractions to equivalent fractions with the common denominator, and then compare the numerators.
10.2 What is the easiest way to compare fractions?
Converting fractions to decimals is often the easiest way to compare them, especially if you have a calculator.
10.3 Can I use cross-multiplication to compare fractions?
Yes, cross-multiplication is a quick method to compare two fractions.
10.4 What is the LCM method for comparing fractions?
The LCM method involves finding the least common multiple of the denominators and converting the fractions to equivalent fractions with the LCM as the denominator.
10.5 How do I compare multiple fractions with different denominators?
Find the LCM of all the denominators and convert each fraction to an equivalent fraction with the LCM as the denominator. Then, compare the numerators.
10.6 What are benchmark fractions and how do I use them?
Benchmark fractions like 0, 1/2, and 1 can be used as reference points to compare fractions. Assess whether each fraction is closer to 0, 1/2, or 1 and use these benchmarks to make comparisons.
10.7 How do I compare mixed numbers?
Convert the mixed numbers to improper fractions and then compare as usual, or compare the whole numbers first and then the fractional parts if the whole numbers are the same.
10.8 How do I deal with negative fractions when comparing?
Remember that the fraction with the “smaller” negative value is actually larger. For example, -1/4 > -1/2.
10.9 What are some common mistakes to avoid when comparing fractions?
Avoid assuming that a larger denominator means a larger fraction, incorrectly applying cross-multiplication, forgetting to find a common denominator, and not simplifying fractions first.
10.10 Why is comparing fractions important in real life?
Comparing fractions is essential in various real-life situations, such as cooking, finance, construction, and education.
11. Conclusion: Mastering Fraction Comparison with COMPARE.EDU.VN
Comparing fractions with different denominators doesn’t have to be a daunting task. With the right methods and a bit of practice, you can confidently compare fractions and apply this skill in various real-world scenarios. At COMPARE.EDU.VN, we’re dedicated to providing you with the resources and guidance you need to excel in mathematics.
Ready to take your fraction comparison skills to the next level? Explore COMPARE.EDU.VN today and discover more tools, examples, and expert advice to help you master this essential concept.
For more information, visit our website at COMPARE.EDU.VN or contact us at 333 Comparison Plaza, Choice City, CA 90210, United States. You can also reach us via WhatsApp at +1 (626) 555-9090. Let compare.edu.vn be your trusted resource for making informed decisions and mastering essential skills.