How Does The Mean Compare To The Median in statistical analysis, and why is understanding this difference crucial for data interpretation? COMPARE.EDU.VN offers comprehensive comparisons to help you make informed decisions. Dive into this detailed examination to uncover the nuances between these two measures of central tendency and learn when to use each effectively, exploring central tendency measures, data distribution, and statistical analysis.
1. Understanding Mean and Median: Core Concepts
The mean and median are both measures of central tendency used to summarize a dataset. While they both aim to represent the “typical” value, they do so in fundamentally different ways. Understanding these differences is crucial for accurate data interpretation.
1.1. What is the Mean?
The mean, often referred to as the average, is calculated by summing all the values in a dataset and dividing by the number of values.
Formula:
Mean = (Sum of all values) / (Number of values)
Example:
Consider the dataset: 2, 4, 6, 8, 10
Mean = (2 + 4 + 6 + 8 + 10) / 5 = 30 / 5 = 6
The mean is sensitive to every value in the dataset, making it susceptible to outliers (extreme values).
1.2. What is the Median?
The median is the middle value in a dataset when the values are arranged in ascending or descending order.
How to Find the Median:
- Order the data: Arrange the dataset from smallest to largest.
- Odd number of values: If there is an odd number of values, the median is the middle value.
- Even number of values: If there is an even number of values, the median is the average of the two middle values.
Example 1 (Odd Number of Values):
Consider the dataset: 2, 4, 6, 8, 10
Ordered dataset: 2, 4, 6, 8, 10
Median = 6
Example 2 (Even Number of Values):
Consider the dataset: 2, 4, 6, 8
Ordered dataset: 2, 4, 6, 8
Median = (4 + 6) / 2 = 5
The median is not affected by extreme values, making it a more robust measure of central tendency for skewed distributions.
1.3. Key Differences Summarized
| Feature | Mean | Median |
|---|---|---|
| Calculation | Sum of values divided by the number of values | Middle value in an ordered dataset |
| Sensitivity | Sensitive to all values, including outliers | Not sensitive to extreme values or outliers |
| Best Used For | Symmetrical distributions | Skewed distributions |
| Interpretation | Average value | Middle value |


2. Understanding Data Distributions
Data distribution plays a critical role in determining whether the mean or median is a more appropriate measure of central tendency. Different types of distributions can significantly impact the relationship between the mean and the median.
2.1. Symmetrical Distributions
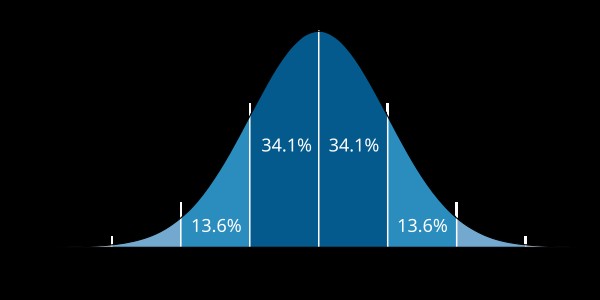
In a symmetrical distribution, the data is evenly distributed around the center. The left and right sides of the distribution are mirror images of each other.
Characteristics of Symmetrical Distributions:
- Mean ≈ Median: In a perfectly symmetrical distribution, the mean and median are equal.
- Bell-shaped curve: Many symmetrical distributions follow a bell-shaped curve, also known as a normal distribution.
Examples:
- Height of adults
- IQ scores
Alt text: Normal distribution bell curve with mean and median at center.
In symmetrical distributions, the mean is a good representation of the central tendency because it accurately reflects the balance of the data.
2.2. Skewed Distributions
A skewed distribution is asymmetrical, meaning the data is concentrated on one side of the distribution.
Types of Skewness:
- Right Skew (Positive Skew): The tail extends to the right, indicating a few high values. The mean is greater than the median.
- Left Skew (Negative Skew): The tail extends to the left, indicating a few low values. The mean is less than the median.
Right Skew (Positive Skew):
Alt text: Right-skewed distribution graph showing the tail extending to the right.
- Mean > Median
- Examples: Income distribution (a few high earners pull the mean upward), house prices (a few expensive houses inflate the mean)
Left Skew (Negative Skew):
Alt text: Left-skewed distribution graph illustrating the tail extending to the left.
- Mean < Median
- Examples: Age at death (most people live to old age, with fewer dying young), exam scores (if an exam is easy, most students score high, with fewer scoring low)
2.3. Impact of Outliers
Outliers are extreme values that lie far from the other values in a dataset. They can significantly affect the mean but have little impact on the median.
Effect on the Mean:
Outliers pull the mean towards their direction. In a right-skewed distribution, high outliers increase the mean. In a left-skewed distribution, low outliers decrease the mean.
Effect on the Median:
The median is resistant to outliers because it only considers the middle value(s). Extreme values do not change the position of the median.
Example:
Consider the dataset: 10, 12, 14, 16, 100
- Mean = (10 + 12 + 14 + 16 + 100) / 5 = 152 / 5 = 30.4
- Median = 14
In this case, the outlier (100) significantly inflates the mean, while the median remains a more representative measure of central tendency.
2.4. Choosing the Right Measure
When choosing between the mean and median, consider the shape of the distribution and the presence of outliers:
- Symmetrical Distribution: Use the mean, as it accurately reflects the central tendency.
- Skewed Distribution: Use the median, as it is less affected by extreme values and provides a more robust measure of the typical value.
- Outliers Present: Use the median to avoid distortion caused by extreme values.
Understanding data distributions and the impact of outliers is essential for selecting the most appropriate measure of central tendency. COMPARE.EDU.VN provides tools and resources to help you analyze and interpret data effectively.
3. Practical Examples: Mean vs. Median
To further illustrate the differences between the mean and median, let’s explore practical examples across various fields.
3.1. Income Distribution
Income distribution is often right-skewed, with a few high earners and many people earning less.
Example:
Consider a small company with the following salaries:
- Employee 1: $40,000
- Employee 2: $45,000
- Employee 3: $50,000
- Employee 4: $55,000
- CEO: $500,000
Calculations:
- Mean = ($40,000 + $45,000 + $50,000 + $55,000 + $500,000) / 5 = $138,000
- Median = $50,000
Interpretation:
The mean salary is $138,000, which is significantly higher than most employees’ salaries. The median salary is $50,000, which better represents the typical salary in the company. In this case, the median is a more appropriate measure of central tendency due to the influence of the CEO’s high salary.
3.2. Real Estate Prices
Real estate prices can also be right-skewed, with a few very expensive properties and many moderately priced homes.
Example:
Consider the prices of houses in a neighborhood:
- House 1: $200,000
- House 2: $250,000
- House 3: $300,000
- House 4: $350,000
- House 5: $1,000,000
Calculations:
- Mean = ($200,000 + $250,000 + $300,000 + $350,000 + $1,000,000) / 5 = $420,000
- Median = $300,000
Interpretation:
The mean house price is $420,000, which is higher than most of the houses in the neighborhood. The median house price is $300,000, which provides a more accurate representation of the typical house price. Again, the median is a better measure due to the presence of a high-priced outlier.
3.3. Exam Scores
Exam scores can be either symmetrical or skewed, depending on the difficulty of the exam.
Example 1 (Symmetrical Distribution):
Consider exam scores: 70, 75, 80, 85, 90
Calculations:
- Mean = (70 + 75 + 80 + 85 + 90) / 5 = 80
- Median = 80
Interpretation:
The mean and median are both 80, indicating a symmetrical distribution. In this case, the mean is an appropriate measure of central tendency.
Example 2 (Left-Skewed Distribution):
Consider exam scores: 90, 92, 95, 98, 98
Calculations:
- Mean = (90 + 92 + 95 + 98 + 98) / 5 = 94.6
- Median = 95
Interpretation:
The mean is 94.6, and the median is 95. The mean is slightly lower than the median due to the left-skewed distribution (most scores are high, with a few lower scores). The median may be a slightly better representation in this case.
3.4. Waiting Times
Waiting times in service industries can often be right-skewed, with most customers waiting a short time and a few waiting much longer.
Example:
Consider waiting times (in minutes) at a customer service call center:
- 2, 3, 4, 5, 30
Calculations:
- Mean = (2 + 3 + 4 + 5 + 30) / 5 = 44 / 5 = 8.8 minutes
- Median = 4 minutes
Interpretation:
The mean waiting time is 8.8 minutes, which is skewed upward by the one customer who waited 30 minutes. The median waiting time is 4 minutes, which gives a better indication of how long a typical customer waits.
3.5. Summary Table of Examples
| Scenario | Distribution | Mean | Median | Best Measure |
|---|---|---|---|---|
| Income Distribution | Right-Skewed | $138,000 | $50,000 | Median |
| Real Estate Prices | Right-Skewed | $420,000 | $300,000 | Median |
| Exam Scores (1) | Symmetrical | 80 | 80 | Mean |
| Exam Scores (2) | Left-Skewed | 94.6 | 95 | Median |
| Waiting Times | Right-Skewed | 8.8 minutes | 4 minutes | Median |
These practical examples illustrate how the choice between the mean and median depends on the shape of the data distribution and the presence of outliers. Use COMPARE.EDU.VN to analyze your data and make informed decisions.
4. Advantages and Disadvantages
Choosing between the mean and median involves weighing their respective advantages and disadvantages in the context of the specific dataset.
4.1. Advantages of the Mean
- Uses all data values: The mean incorporates every value in the dataset, providing a comprehensive summary.
- Familiar and widely understood: The mean is a commonly used and easily understood measure of central tendency.
- Useful for further statistical analysis: The mean is often used in more advanced statistical calculations and models.
4.2. Disadvantages of the Mean
- Sensitive to outliers: The mean can be significantly affected by extreme values, leading to a distorted representation of the typical value.
- Not suitable for skewed distributions: In skewed distributions, the mean can be misleading and not accurately reflect the center of the data.
4.3. Advantages of the Median
- Resistant to outliers: The median is not affected by extreme values, making it a robust measure of central tendency.
- Suitable for skewed distributions: The median provides a more accurate representation of the typical value in skewed distributions.
- Easy to understand and calculate: The median is simple to calculate and interpret, especially for small datasets.
4.4. Disadvantages of the Median
- Ignores some data values: The median only considers the middle value(s) and ignores the rest of the data, potentially losing some information.
- Less useful for further statistical analysis: The median is not as commonly used as the mean in advanced statistical calculations.
- May not be representative in symmetrical distributions: In symmetrical distributions, the mean is often a better representation of the central tendency.
4.5. Summary Table of Advantages and Disadvantages
| Feature | Mean | Median |
|---|---|---|
| Advantages | Uses all data values, familiar, useful for further analysis | Resistant to outliers, suitable for skewed distributions, easy to understand |
| Disadvantages | Sensitive to outliers, not suitable for skewed distributions | Ignores some data values, less useful for further analysis, may not be representative in symmetrical distributions |
Consider these advantages and disadvantages when deciding whether to use the mean or median for your data analysis. COMPARE.EDU.VN offers resources to help you evaluate the best measure for your specific needs.
5. Formulas and Calculations
Understanding the formulas and calculations for the mean and median is essential for accurate data analysis.
5.1. Mean Formula
The formula for the mean is straightforward:
Mean = (Sum of all values) / (Number of values)
Mathematical Notation:
μ = (∑ xᵢ) / n
Where:
- μ = Mean
- ∑ xᵢ = Sum of all values in the dataset
- n = Number of values in the dataset
Example:
Consider the dataset: 3, 5, 7, 9, 11
- Sum of values = 3 + 5 + 7 + 9 + 11 = 35
- Number of values = 5
- Mean = 35 / 5 = 7
5.2. Median Calculation
The method for calculating the median depends on whether the dataset has an odd or even number of values.
Odd Number of Values:
- Order the data: Arrange the dataset from smallest to largest.
- Identify the middle value: The median is the middle value.
Example:
Consider the dataset: 3, 5, 7, 9, 11
Ordered dataset: 3, 5, 7, 9, 11
Median = 7
Even Number of Values:
- Order the data: Arrange the dataset from smallest to largest.
- Identify the two middle values: The median is the average of the two middle values.
Example:
Consider the dataset: 3, 5, 7, 9
Ordered dataset: 3, 5, 7, 9
Median = (5 + 7) / 2 = 6
5.3. Weighted Mean
In some cases, each value in a dataset may have a different weight or importance. The weighted mean takes these weights into account.
Formula:
Weighted Mean = (∑ (wᵢ * xᵢ)) / (∑ wᵢ)
Where:
- wᵢ = Weight of each value
- xᵢ = Value
- ∑ (wᵢ * xᵢ) = Sum of the product of weights and values
- ∑ wᵢ = Sum of the weights
Example:
Consider a student’s grades:
- Homework: 90 (weight = 20%)
- Midterm: 80 (weight = 30%)
- Final Exam: 95 (weight = 50%)
Weighted Mean = (0.20 * 90) + (0.30 * 80) + (0.50 * 95) = 18 + 24 + 47.5 = 89.5
5.4. Geometric Mean
The geometric mean is used to find the average rate of change over multiple periods.
Formula:
Geometric Mean = (x₁ * x₂ * … * xₙ)^(1/n)
Where:
- x₁, x₂, …, xₙ = Values
- n = Number of values
Example:
Consider investment returns over three years: 5%, 10%, 15%
Geometric Mean = (1.05 * 1.10 * 1.15)^(1/3) – 1 = (1.32975)^(1/3) – 1 ≈ 1.097 – 1 = 0.097 = 9.7%
The geometric mean provides a more accurate representation of average growth rates than the arithmetic mean (simple average).
5.5. Harmonic Mean
The harmonic mean is used to find the average of rates or ratios.
Formula:
Harmonic Mean = n / (∑ (1 / xᵢ))
Where:
- n = Number of values
- xᵢ = Value
Example:
Consider a car traveling 120 miles at 40 mph and returning at 60 mph.
Harmonic Mean = 2 / ((1/40) + (1/60)) = 2 / (0.025 + 0.0167) = 2 / 0.0417 ≈ 48 mph
The harmonic mean provides a more accurate average speed than the arithmetic mean.
Understanding these formulas and calculations allows you to apply the mean and median effectively in various statistical analyses. Visit COMPARE.EDU.VN for additional tools and resources to enhance your data interpretation skills.
6. Use Cases: When to Use Mean and Median
The choice between the mean and median depends on the context of the data and the goals of the analysis. Here are several use cases to guide your decision.
6.1. Finance and Economics
- Income Analysis: Use the median to represent typical income levels, as income distributions are often right-skewed due to high earners.
- Real Estate Valuation: Use the median to represent typical house prices, as real estate prices can be skewed by expensive properties.
- Investment Returns: Use the geometric mean to calculate average investment returns over multiple periods, providing a more accurate representation of growth rates.
6.2. Healthcare
- Patient Wait Times: Use the median to represent typical wait times in clinics or hospitals, as wait times can be skewed by a few long waits.
- Medical Test Results: If test results are normally distributed, the mean can be used. If skewed, the median provides a better representation.
- Survival Analysis: Use the median survival time to indicate the time at which half of the patients have survived, particularly useful when survival times are skewed.
6.3. Education
- Exam Scores: If exam scores are symmetrical, use the mean to represent the average performance. If skewed (e.g., an easy exam with mostly high scores), the median is more appropriate.
- Student Demographics: Use the median to represent typical age or grade levels, especially in diverse populations.
- Teacher Evaluations: Use the median to summarize teacher evaluation scores, as outliers (very high or very low scores) can distort the mean.
6.4. Marketing and Sales
- Customer Spending: Use the median to represent typical customer spending, as spending can be skewed by a few high-value customers.
- Website Traffic: Use the median to represent typical page views or session durations, as outliers (popular pages or long sessions) can distort the mean.
- Sales Performance: Use the median to represent typical sales performance across a team, as sales figures can be skewed by a few top performers.
6.5. Environmental Science
- Pollution Levels: Use the median to represent typical pollution levels, as extreme pollution events can skew the mean.
- Rainfall Data: Use the median to represent typical rainfall amounts, as occasional heavy rains can distort the mean.
- Temperature Readings: If temperature data is normally distributed, the mean can be used. If skewed, the median provides a better representation.
6.6. Summary Table of Use Cases
| Field | Scenario | Use Case | Measure | Justification |
|---|---|---|---|---|
| Finance and Economics | Income Analysis | Represent typical income levels | Median | Income distributions are often right-skewed due to high earners. |
| Finance and Economics | Real Estate Valuation | Represent typical house prices | Median | Real estate prices can be skewed by expensive properties. |
| Healthcare | Patient Wait Times | Represent typical wait times in clinics or hospitals | Median | Wait times can be skewed by a few long waits. |
| Healthcare | Medical Test Results | Represent central tendency of test results | Mean/Median | Use mean if normally distributed; use median if skewed. |
| Education | Exam Scores | Represent average performance on exams | Mean/Median | Use mean if scores are symmetrical; use median if skewed (e.g., easy exam). |
| Marketing and Sales | Customer Spending | Represent typical customer spending | Median | Spending can be skewed by a few high-value customers. |
| Environmental Science | Pollution Levels | Represent typical pollution levels | Median | Extreme pollution events can skew the mean. |
| General | Data with Outliers | Summarize data where extreme values are present | Median | The median is resistant to outliers, providing a more robust measure of central tendency. |
| General | Symmetrical Data | Summarize data with a balanced distribution | Mean | The mean accurately reflects the central tendency in symmetrical distributions. |
| General | Skewed Data | Summarize data where values are concentrated on one side | Median | The median provides a more accurate representation of the typical value in skewed distributions. |
These use cases illustrate how to select the appropriate measure of central tendency based on the data’s characteristics and the goals of the analysis. Rely on COMPARE.EDU.VN to help you analyze and interpret your data effectively.
7. Visualizing Mean and Median
Visualizing the mean and median can provide valuable insights into the distribution of data.
7.1. Histograms
Histograms are a common way to visualize data distributions. They display the frequency of values within specific ranges or bins.
Symmetrical Distribution:
In a symmetrical histogram, the mean and median are located at the center of the distribution.
Alt text: Symmetrical histogram showing the mean and median at the center.
Skewed Distribution:
In a right-skewed histogram, the mean is pulled to the right by the tail, while the median remains closer to the peak.
Alt text: Right-skewed histogram showing the mean to the right of the median.
In a left-skewed histogram, the mean is pulled to the left by the tail, while the median remains closer to the peak.
Alt text: Left-skewed histogram illustrating the mean to the left of the median.
7.2. Box Plots
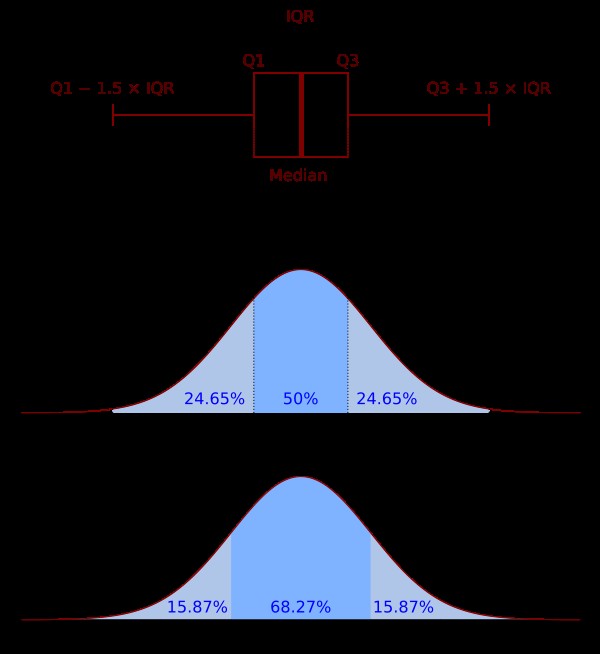
Box plots (also known as box-and-whisker plots) provide a visual summary of the data’s distribution, including the median, quartiles, and outliers.
Components of a Box Plot:
- Median: The line inside the box represents the median.
- Quartiles: The box represents the interquartile range (IQR), which contains the middle 50% of the data.
- Whiskers: The whiskers extend to the furthest data point within 1.5 times the IQR from the quartiles.
- Outliers: Points outside the whiskers are considered outliers.
Symmetrical Distribution:
In a symmetrical box plot, the median is centered in the box, and the whiskers are roughly equal in length.
Alt text: Symmetrical box plot displaying the median at the center.
Skewed Distribution:
In a skewed box plot, the median is not centered in the box, and the whiskers are unequal in length. Outliers may be present on one side of the box plot.
Alt text: Skewed box plot showing the median off-center and unequal whisker lengths.
7.3. Dot Plots
Dot plots display each data point as a dot along a number line. They are useful for visualizing the distribution of small datasets and identifying clusters and outliers.
Symmetrical Distribution:
In a symmetrical dot plot, the dots are evenly distributed around the center.
Alt text: Symmetrical dot plot with data points evenly distributed.
Skewed Distribution:
In a skewed dot plot, the dots are concentrated on one side, with a tail extending to the other side.
Alt text: Skewed dot plot showing data points concentrated on one side.
7.4. Comparing Visualizations
| Visualization | Symmetrical Distribution | Skewed Distribution |
|---|---|---|
| Histogram | Mean and median at the center | Mean pulled towards the tail; median closer to the peak |
| Box Plot | Median centered in the box; whiskers roughly equal | Median not centered; whiskers unequal; outliers may be present |
| Dot Plot | Dots evenly distributed around the center | Dots concentrated on one side with a tail extending to the other |
Visualizing the mean and median can help you understand the shape of the data distribution and choose the most appropriate measure of central tendency. COMPARE.EDU.VN provides tools for creating these visualizations and analyzing your data.
8. Advanced Considerations
Beyond the basics, there are advanced statistical concepts and techniques that can further refine your understanding of the mean and median.
8.1. Trimmed Mean
The trimmed mean is a modified version of the mean that excludes a certain percentage of the extreme values from both ends of the dataset. This reduces the impact of outliers while still utilizing most of the data.
Calculation:
- Determine the trim percentage: For example, a 10% trimmed mean excludes the top and bottom 10% of the values.
- Order the data: Arrange the dataset from smallest to largest.
- Remove the extreme values: Exclude the specified percentage of values from each end.
- Calculate the mean: Calculate the mean of the remaining values.
Example:
Consider the dataset: 2, 4, 6, 8, 10, 12, 14, 16, 18, 100 (10 values)
Calculate a 10% trimmed mean:
- Trim percentage: 10%
- Values to remove: 10% of 10 = 1 value from each end
- Trimmed dataset: 4, 6, 8, 10, 12, 14, 16, 18
- Trimmed mean = (4 + 6 + 8 + 10 + 12 + 14 + 16 + 18) / 8 = 88 / 8 = 11
The trimmed mean provides a balance between the sensitivity of the mean and the robustness of the median.
8.2. Winsorized Mean
The Winsorized mean is another modified version of the mean that replaces a certain percentage of the extreme values with the nearest remaining values. This also reduces the impact of outliers.
Calculation:
- Determine the Winsorize percentage: For example, a 10% Winsorized mean replaces the top and bottom 10% of the values.
- Order the data: Arrange the dataset from smallest to largest.
- Replace the extreme values: Replace the specified percentage of values from each end with the nearest remaining values.
- Calculate the mean: Calculate the mean of the modified values.
Example:
Consider the dataset: 2, 4, 6, 8, 10, 12, 14, 16, 18, 100 (10 values)
Calculate a 10% Winsorized mean:
- Winsorize percentage: 10%
- Values to replace: 10% of 10 = 1 value from each end
- Winsorized dataset: 4, 4, 6, 8, 10, 12, 14, 16, 18, 18
- Winsorized mean = (4 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 18) / 10 = 110 / 10 = 11
The Winsorized mean is less sensitive to outliers than the mean but still incorporates all data values.
8.3. Using Both Mean and Median
In some cases, it can be informative to report both the mean and median to provide a more complete picture of the data.
When to Use Both:
- Comparing Distributions: Reporting both measures allows for a comparison of the symmetry or skewness of the distribution.
- Highlighting Outliers: A large difference between the mean and median can indicate the presence of outliers and their impact on the mean.
- Communicating Results: Providing both measures can cater to different audiences and ensure that the information is accessible and understandable.
8.4. Statistical Software
Statistical software packages like R, Python (with libraries like NumPy and SciPy), and SPSS provide tools for calculating the mean, median, and other measures of central tendency. They also offer functions for creating visualizations and performing more advanced statistical analyses.
Example (Python with NumPy):
import numpy as np
data = [2, 4, 6, 8, 10, 12, 14, 16, 18, 100]
mean = np.mean(data)
median = np.median(data)
print("Mean:", mean)
print("Median:", median)8.5. Confidence Intervals
A confidence interval provides a range of values within which the true population mean or median is likely to fall. Confidence intervals can help you assess the precision of your estimates and make more informed decisions.
Calculating Confidence Intervals:
- Mean: Use the t-distribution to calculate the confidence interval for the mean, especially for small sample sizes.
- Median: Use bootstrapping or other non-parametric methods to calculate the confidence interval for the median.
These advanced considerations can further enhance your understanding of the mean and median and improve your data analysis skills. Visit compare.edu.vn for more advanced resources and tools.
9. Common Misconceptions
Several misconceptions surround the mean and median. Clearing these up will lead to a better understanding of when to use each.
9.1. The Mean is Always Better
Misconception: The mean is always the best measure of central tendency.
Reality: The mean is only the best measure for symmetrical distributions without significant outliers. In skewed distributions or when outliers are present, the median provides a more accurate representation of the typical value.
9.2. The Median is Just the “Middle Number”
Misconception: The median is simply the middle number in any dataset.
Reality: The median is the middle value only after the dataset has been ordered from smallest to largest. Ordering the data is a crucial step in finding the median.