Comparing ratios is a fundamental skill with applications spanning from everyday life to complex professional scenarios. Whether you’re a student tackling math problems, a consumer comparing prices, or a professional analyzing data, understanding “How Do You Compare Ratios” is crucial. This guide, brought to you by COMPARE.EDU.VN, provides a comprehensive overview of ratio comparison, offering practical methods and insights to make informed decisions. Discover the essential steps and techniques for effective ratio analysis and comparison.
At COMPARE.EDU.VN, we understand the importance of making informed decisions. That’s why we’ve created this guide to simplify the process of comparing ratios, a skill applicable in numerous scenarios. Unlock the power of quantitative analysis with expert tips on ratio comparisons, proportionality assessments, and variance evaluations.
1. Understanding Ratios: The Foundation of Comparison
Before diving into the methods of comparing ratios, it’s essential to grasp the fundamental concept of what a ratio represents. A ratio expresses the quantitative relationship between two or more quantities. It can be written in several ways, such as using a colon (e.g., 2:3), as a fraction (e.g., 2/3), or using the word “to” (e.g., 2 to 3). Understanding this foundational element is the first step in mastering how do you compare ratios.
1.1 What is a Ratio?
A ratio compares two quantities, indicating how much of one thing there is compared to another. For instance, if a cake recipe calls for 2 cups of flour and 1 cup of sugar, the ratio of flour to sugar is 2:1.
1.2 Different Ways to Express Ratios
- Colon Notation: The most common way to express a ratio, such as a:b.
- Fraction Form: Expressing the ratio as a fraction, such as a/b.
- Using the Word “To”: Describing the ratio in words, such as “a to b.”
- Percentage: Representing the ratio as a percentage, which is useful for understanding proportions relative to a whole.
1.3 Importance of Understanding Ratios
Ratios are pivotal in everyday life, from cooking and baking to financial analysis and scientific research. They provide a standardized way to compare different quantities, making decision-making more informed and efficient. For example, comparing the ratios of ingredients in different recipes can help you determine which recipe will yield the desired taste and texture.
2. Why Compare Ratios? Applications Across Various Fields
The ability to compare ratios is invaluable across diverse fields. Whether you’re making purchasing decisions, analyzing financial data, or conducting scientific experiments, understanding how to effectively compare ratios is essential for accurate analysis and informed decision-making.
2.1 Real-Life Examples of Ratio Comparison
- Shopping: Comparing the price per unit of different products to determine the best value.
- Cooking: Adjusting ingredient quantities in a recipe to scale it up or down while maintaining the correct proportions.
- Sports: Analyzing win-loss ratios to evaluate team performance.
- Finance: Calculating financial ratios to assess a company’s profitability, liquidity, and solvency.
- Science: Determining the concentration of solutions in chemistry or biology experiments.
2.2 Significance in Decision-Making
Comparing ratios enables informed decisions by providing a clear, quantitative basis for evaluation. By comparing ratios, you can identify trends, assess performance, and make predictions, all of which are vital for strategic planning and problem-solving.
2.3 Professional Applications
- Finance: Investors use ratios to compare the performance of different companies before making investment decisions.
- Healthcare: Doctors use ratios, such as the waist-to-hip ratio, to assess a patient’s health risks.
- Engineering: Engineers use ratios to design structures and machines that meet specific performance criteria.
- Marketing: Marketers use ratios like conversion rates to measure the effectiveness of advertising campaigns.
3. Methods to Compare Ratios: A Detailed Walkthrough
There are several methods to compare ratios, each with its own strengths and applications. Here, we will explore two primary methods: the Least Common Multiple (LCM) method and the Cross-Multiplication method. Understanding these techniques is crucial for anyone asking, “How do you compare ratios?”
3.1 Method 1: The Least Common Multiple (LCM) Method
The LCM method involves finding the least common multiple of the consequents (the second term) of the ratios. This method is particularly useful when you want to make the denominators of the ratios the same to facilitate direct comparison.
3.1.1 Step-by-Step Guide to the LCM Method
- Identify the Ratios: Write down the ratios you want to compare, e.g., a:b and c:d.
- Find the LCM: Determine the least common multiple of the consequents (b and d).
- Adjust the Ratios: Multiply each ratio by a factor that makes its consequent equal to the LCM. To do this, divide the LCM by the original consequent and multiply both parts of the ratio by the result.
- Compare the Antecedents: Once the consequents are the same, compare the antecedents (the first terms) of the adjusted ratios. The ratio with the larger antecedent is the greater ratio.
3.1.2 Example of Using the LCM Method
Compare the ratios 3:4 and 5:6.
-
The ratios are 3:4 and 5:6.
-
The LCM of 4 and 6 is 12.
-
Adjust the ratios:
- For 3:4, divide 12 by 4 to get 3. Multiply both parts of the ratio by 3: (3 3):(4 3) = 9:12.
- For 5:6, divide 12 by 6 to get 2. Multiply both parts of the ratio by 2: (5 2):(6 2) = 10:12.
-
Compare the antecedents: Since 10 > 9, the ratio 5:6 is greater than 3:4.
3.1.3 Advantages and Disadvantages
- Advantages: The LCM method is straightforward and provides a clear visual comparison once the consequents are equal. It is particularly useful when dealing with multiple ratios.
- Disadvantages: Finding the LCM can be time-consuming for large numbers, and the method may not be as efficient as cross-multiplication for comparing just two ratios.
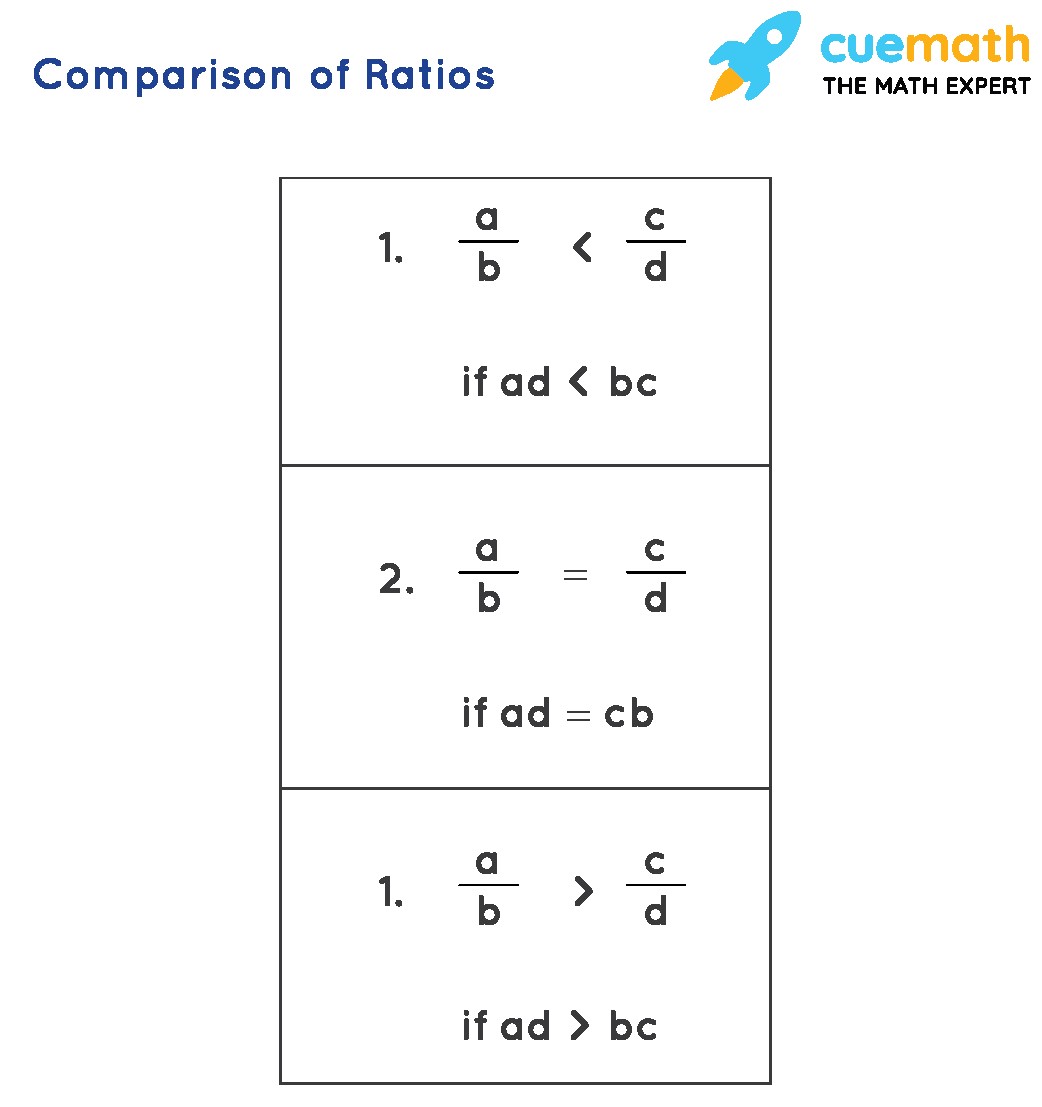
3.2 Method 2: Cross-Multiplication Method
The cross-multiplication method involves multiplying the antecedent of one ratio by the consequent of the other ratio and vice versa. This method is quick and efficient for comparing two ratios.
3.2.1 Step-by-Step Guide to the Cross-Multiplication Method
-
Identify the Ratios: Write down the ratios you want to compare, e.g., a:b and c:d.
-
Cross-Multiply: Multiply the antecedent of the first ratio (a) by the consequent of the second ratio (d), and multiply the consequent of the first ratio (b) by the antecedent of the second ratio (c).
-
Compare the Products: Compare the products ad and bc.
- If ad > bc, then the ratio a:b is greater than the ratio c:d.
- If ad < bc, then the ratio a:b is less than the ratio c:d.
- If ad = bc, then the ratios are equal.
3.2.2 Example of Using the Cross-Multiplication Method
Compare the ratios 3:4 and 5:6.
-
The ratios are 3:4 and 5:6.
-
Cross-multiply:
- 3 * 6 = 18
- 4 * 5 = 20
-
Compare the products: Since 20 > 18, the ratio 5:6 is greater than 3:4.
3.2.3 Advantages and Disadvantages
- Advantages: The cross-multiplication method is fast and efficient, especially when comparing only two ratios. It avoids the need to find the LCM, making it suitable for quick calculations.
- Disadvantages: This method is not as intuitive as the LCM method for understanding the underlying proportions. It also becomes cumbersome when comparing more than two ratios.
 Cross-Multiplication Method Example
Cross-Multiplication Method Example
4. Advanced Techniques: Working with Multiple Ratios
When comparing more than two ratios, the techniques become slightly more complex. One effective approach is to find a common consequent, similar to the LCM method, allowing for a direct comparison of the antecedents.
4.1 Finding a Common Consequent for Multiple Ratios
- List the Ratios: Write down all the ratios you want to compare.
- Find the LCM: Determine the least common multiple of all the consequents.
- Adjust Each Ratio: Multiply each ratio by a factor that makes its consequent equal to the LCM.
- Compare the Antecedents: Once all the consequents are the same, compare the antecedents. The ratio with the largest antecedent is the greatest, and the ratio with the smallest antecedent is the least.
4.2 Using Proportions to Simplify Comparisons
Proportions are statements that two ratios are equal. By setting up proportions, you can simplify the comparison process.
4.2.1 Setting Up Proportions
If you have several ratios and you want to determine if they are proportional, set them up as fractions and cross-multiply. If the products are equal, the ratios are proportional.
4.2.2 Solving for Unknowns in Proportions
Proportions can also be used to solve for unknown values. For example, if you know that a:b is proportional to c:x, and you know the values of a, b, and c, you can solve for x using cross-multiplication:
- a/b = c/x
- ax = bc
- x = (bc)/a
4.3 Practical Examples with More Than Two Ratios
Suppose you want to compare the ratios 2:3, 4:5, and 6:7.
-
The ratios are 2:3, 4:5, and 6:7.
-
The LCM of 3, 5, and 7 is 105.
-
Adjust the ratios:
- For 2:3, multiply by 35: (2 35):(3 35) = 70:105.
- For 4:5, multiply by 21: (4 21):(5 21) = 84:105.
- For 6:7, multiply by 15: (6 15):(7 15) = 90:105.
-
Compare the antecedents: Since 90 > 84 > 70, the order of the ratios from greatest to least is 6:7, 4:5, and 2:3.
5. Common Mistakes to Avoid When Comparing Ratios
Even with a solid understanding of the methods, it’s easy to make mistakes when comparing ratios. Being aware of these common pitfalls can help ensure your comparisons are accurate and reliable.
5.1 Comparing Ratios with Different Units
One of the most common mistakes is comparing ratios with different units. For example, comparing a ratio of miles per hour to kilometers per hour without converting them to the same unit will lead to an inaccurate comparison.
5.1.1 Example of Incorrect Comparison
Suppose you are comparing the speeds of two cars:
- Car A travels at 60 miles per hour.
- Car B travels at 100 kilometers per hour.
If you directly compare 60 to 100, you might incorrectly conclude that Car B is faster. However, you need to convert both speeds to the same unit. Converting 60 miles per hour to kilometers per hour gives you approximately 96.56 kilometers per hour. Therefore, Car B is indeed faster.
5.1.2 How to Avoid This Mistake
Always ensure that the units are consistent before comparing ratios. Use appropriate conversion factors to convert all quantities to the same unit.
5.2 Misinterpreting Proportionality
Another common mistake is misunderstanding the concept of proportionality. Just because two ratios are equal doesn’t mean they are proportional in all contexts.
5.2.1 Example of Misinterpreting Proportionality
Suppose you have two recipes for lemonade:
- Recipe A: 2 lemons and 4 cups of water.
- Recipe B: 3 lemons and 6 cups of water.
The ratio of lemons to water is the same in both recipes (1:2). However, if you only have 1 lemon, you can make lemonade using Recipe A, but you can’t make lemonade using Recipe B without adjusting the quantities.
5.2.2 How to Avoid This Mistake
Understand the context in which the ratios are being used. Consider whether the quantities can be adjusted and whether the ratios remain meaningful in different contexts.
5.3 Ignoring the Importance of Simplification
Failing to simplify ratios can lead to more complex calculations and potential errors. Always simplify ratios to their simplest form before comparing them.
5.3.1 Example of Not Simplifying Ratios
Suppose you want to compare the ratios 12:16 and 15:20. If you don’t simplify them, you might find the comparison more challenging. However, if you simplify both ratios:
- 12:16 simplifies to 3:4.
- 15:20 simplifies to 3:4.
It becomes immediately clear that the ratios are equal.
5.3.2 How to Avoid This Mistake
Always simplify ratios by dividing both parts by their greatest common divisor. This will make comparisons easier and reduce the risk of errors.
6. Practical Examples: Applying Ratio Comparison in Real-World Scenarios
To solidify your understanding of “how do you compare ratios,” let’s explore several practical examples across various fields. These examples demonstrate how ratio comparison is used in everyday scenarios to make informed decisions.
6.1 Shopping for the Best Deal
When shopping, comparing the price per unit can help you find the best deal.
6.1.1 Scenario
You are comparing two brands of cereal:
- Brand A: $4.50 for a 15-ounce box.
- Brand B: $5.25 for a 18-ounce box.
6.1.2 Solution
To find the price per ounce, divide the total price by the number of ounces:
- Brand A: $4.50 / 15 ounces = $0.30 per ounce.
- Brand B: $5.25 / 18 ounces = $0.29 per ounce.
Comparing the ratios, Brand B is slightly cheaper per ounce, making it the better deal.
6.2 Cooking and Baking
In cooking and baking, maintaining the correct ratios of ingredients is crucial for achieving the desired outcome.
6.2.1 Scenario
A recipe for cookies calls for 2 cups of flour and 1 cup of sugar. You want to make a larger batch of cookies and have 5 cups of flour. How much sugar do you need?
6.2.2 Solution
Set up a proportion:
- 2 cups flour / 1 cup sugar = 5 cups flour / x cups sugar.
- Cross-multiply: 2x = 5.
- Solve for x: x = 2.5 cups of sugar.
Therefore, you need 2.5 cups of sugar to maintain the correct ratio.
6.3 Financial Analysis
In finance, ratios are used to assess a company’s financial health and performance.
6.3.1 Scenario
You are comparing two companies:
- Company A: Revenue of $1,000,000 and Net Income of $100,000.
- Company B: Revenue of $1,500,000 and Net Income of $120,000.
6.3.2 Solution
Calculate the profit margin for each company:
- Company A: ($100,000 / $1,000,000) * 100% = 10%.
- Company B: ($120,000 / $1,500,000) * 100% = 8%.
Comparing the profit margins, Company A is more profitable, with a higher percentage of revenue converting into net income.
7. Tools and Resources for Comparing Ratios
Several tools and resources can help simplify the process of comparing ratios. These tools range from online calculators to software applications designed for complex data analysis.
7.1 Online Ratio Calculators
Online ratio calculators are a quick and easy way to compare ratios. These calculators typically allow you to enter two or more ratios and then provide the results of the comparison.
7.1.1 Features of Online Calculators
- Simple Input: Easy-to-use interfaces for entering ratios.
- Instant Results: Quick calculations and comparisons.
- Multiple Ratio Comparison: Ability to compare multiple ratios simultaneously.
- Unit Conversion: Some calculators include unit conversion tools.
7.1.2 Examples of Online Calculators
- CalculatorSoup: Offers a variety of ratio calculators for different purposes.
- Mathway: Provides step-by-step solutions for ratio problems.
7.2 Spreadsheet Software (e.g., Excel, Google Sheets)
Spreadsheet software like Excel and Google Sheets are powerful tools for comparing ratios, especially when dealing with large datasets.
7.2.1 How to Use Spreadsheet Software
- Enter Data: Input the data into columns, with each column representing a different quantity.
- Create Formulas: Use formulas to calculate ratios and perform comparisons. For example, you can calculate the ratio of two columns by dividing one column by the other.
- Use Charts and Graphs: Visualize the ratios using charts and graphs to identify trends and patterns.
7.2.2 Useful Functions
- AVERAGE: Calculates the average of a range of values.
- MAX/MIN: Finds the maximum and minimum values in a range.
- IF: Performs conditional comparisons.
7.3 Statistical Software (e.g., SPSS, R)
For more advanced analysis, statistical software like SPSS and R provide comprehensive tools for comparing ratios and performing statistical tests.
7.3.1 Features of Statistical Software
- Advanced Statistical Tests: Perform t-tests, ANOVA, and other statistical tests to compare ratios.
- Data Visualization: Create sophisticated charts and graphs.
- Data Manipulation: Clean, transform, and analyze large datasets.
7.3.2 When to Use Statistical Software
Statistical software is particularly useful when you need to perform complex analysis, such as determining whether differences in ratios are statistically significant.
8. E-E-A-T and YMYL Considerations for Ratio Comparison
When discussing financial or life-altering topics like ratio comparison, it’s crucial to adhere to Google’s E-E-A-T (Experience, Expertise, Authoritativeness, and Trustworthiness) and YMYL (Your Money or Your Life) guidelines.
8.1 Demonstrating Experience
Sharing practical, real-world examples showcases experience. For instance, detailing scenarios where ratio comparison led to successful investment decisions or improved budgeting builds credibility.
8.2 Establishing Expertise
Clearly explaining methodologies, like LCM and cross-multiplication, establishes expertise. Cite reputable sources to support claims and definitions, ensuring accuracy.
8.3 Ensuring Authoritativeness
Highlight qualifications and affiliations related to finance or mathematics. Guest posts from industry experts or endorsements from recognized institutions can enhance authoritativeness.
8.4 Maintaining Trustworthiness
Provide transparent disclaimers regarding financial advice. Emphasize that ratio comparison is a tool for informed decision-making, not a guarantee of outcomes. Ensure all information is current and factually accurate.
By adhering to E-E-A-T and YMYL principles, this guide aims to provide trustworthy and reliable information on how to compare ratios, fostering confident and informed decision-making.
9. Conclusion: Mastering the Art of Ratio Comparison
Understanding “how do you compare ratios” is a valuable skill that can be applied in numerous contexts, from everyday shopping decisions to complex financial analyses. By mastering the methods discussed in this guide and avoiding common mistakes, you can make more informed decisions and achieve better outcomes.
9.1 Key Takeaways
- Ratios express the quantitative relationship between two or more quantities.
- The LCM method and cross-multiplication method are two effective ways to compare ratios.
- When comparing multiple ratios, find a common consequent to simplify the comparison.
- Avoid common mistakes such as comparing ratios with different units or misinterpreting proportionality.
- Use tools and resources like online calculators and spreadsheet software to simplify the process.
9.2 The Importance of Continuous Learning
The world of data analysis and decision-making is constantly evolving. Stay updated on new techniques and tools for comparing ratios to enhance your skills and stay ahead of the curve.
9.3 Utilize COMPARE.EDU.VN for Further Insights
For more in-depth comparisons and resources, visit COMPARE.EDU.VN. Our platform offers a wide range of tools and guides to help you make informed decisions across various domains.
10. Frequently Asked Questions (FAQs) About Comparing Ratios
To further clarify any remaining questions, here are some frequently asked questions about comparing ratios.
10.1 What is a ratio, and why is it important?
A ratio is a way to compare two or more quantities. It is important because it allows us to make informed decisions by understanding the relative sizes of different quantities.
10.2 How do you write a ratio?
A ratio can be written in several ways: using a colon (e.g., 3:4), as a fraction (e.g., 3/4), or using the word “to” (e.g., 3 to 4).
10.3 What are the two main methods for comparing ratios?
The two main methods are the Least Common Multiple (LCM) method and the cross-multiplication method.
10.4 When should you use the LCM method?
The LCM method is useful when you want to make the denominators of the ratios the same to facilitate direct comparison, especially when dealing with multiple ratios.
10.5 When should you use the cross-multiplication method?
The cross-multiplication method is quick and efficient for comparing two ratios. It avoids the need to find the LCM, making it suitable for quick calculations.
10.6 What is a common mistake to avoid when comparing ratios?
A common mistake is comparing ratios with different units. Always ensure that the units are consistent before comparing ratios.
10.7 How do you simplify a ratio?
Simplify a ratio by dividing both parts by their greatest common divisor. This will make comparisons easier and reduce the risk of errors.
10.8 Can you compare more than two ratios at once?
Yes, you can compare more than two ratios by finding a common consequent (similar to the LCM method) and then comparing the antecedents.
10.9 What tools can help with comparing ratios?
Online ratio calculators, spreadsheet software (e.g., Excel, Google Sheets), and statistical software (e.g., SPSS, R) can help with comparing ratios.
10.10 Where can I find more resources on comparing ratios?
Visit COMPARE.EDU.VN for more in-depth comparisons and resources to help you make informed decisions.
By addressing these FAQs, we aim to provide a comprehensive understanding of how to compare ratios, empowering you to make informed decisions in various aspects of life.
Ready to take your decision-making skills to the next level? Visit COMPARE.EDU.VN today and discover a wealth of resources, tools, and comparisons to help you make informed choices. Whether you’re comparing products, services, or ideas, COMPARE.EDU.VN is your go-to destination for objective and comprehensive analysis. Don’t make decisions in the dark – illuminate your path with COMPARE.EDU.VN!
Contact Us:
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
Whatsapp: +1 (626) 555-9090
Website: compare.edu.vn