Comparing fractions can be tricky, but using a number line makes it visual and easier to understand. This article outlines four effective strategies for comparing fractions with unlike denominators using a number line. These methods help students visualize fraction comparisons, building a strong foundation for fraction understanding. They also address key Common Core State Standards for working with fractions in 3rd, 4th, and 5th grades.
Four Strategies for Comparing Fractions on a Number Line
Number lines offer a crucial visual representation of fractions as lengths or distances from zero, similar to whole numbers. This understanding is fundamental for comparing fractions effectively.
1. Equivalent Denominators (Same Size Pieces)
This strategy involves finding a common denominator for both fractions. Once the denominators are the same, the fraction with the larger numerator is the greater fraction. Thinking of denominators as “same size pieces” helps students visualize the comparison.
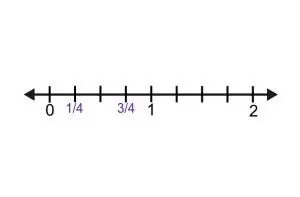
Example: Compare 1/4 and 3/4.
Both fractions are divided into fourths (same size pieces). Since 3 is greater than 1, 3/4 is greater than 1/4.
2. Same Numerator (Same Number of Pieces)
When fractions have the same numerator, focus on the denominators. The fraction with the smaller denominator represents larger pieces, making it the greater fraction.
Example: Compare 3/4 and 3/6.
Both fractions have 3 pieces. However, fourths are larger than sixths, so 3/4 is greater than 3/6.
3. Benchmark Fractions (Comparing to 1/2 or 1)
Compare each fraction to a benchmark fraction like 1/2 or 1. This helps quickly determine which fraction is larger or smaller.
Example: Compare 2/5 and 4/6.
2/5 is less than 1/2, while 4/6 is greater than 1/2. Therefore, 4/6 is greater than 2/5.
4. Missing Pieces (Distance from a Whole)
Analyze how far each fraction is from a whole number (usually 1). The fraction closer to the whole number is the greater fraction.
Example: Compare 3/4 and 7/8.
3/4 is 1/4 away from 1, while 7/8 is 1/8 away from 1. Since 1/8 is smaller than 1/4, 7/8 is closer to 1 and therefore greater than 3/4.
Conclusion
Utilizing number lines to compare fractions provides a concrete and visual way for students to grasp this essential math concept. By practicing these four strategies, students develop a deeper understanding of fractions and their relationships, solidifying their foundational math skills. This visual approach strengthens number sense and facilitates a more intuitive understanding of fraction comparisons.