Comparing and ordering numbers is a fundamental math skill used daily. This involves determining which number is larger, smaller, or equal to another, and then arranging them in a specific sequence. This article will guide you through the process of comparing and ordering numbers, from basic principles to comparing rational numbers.
Understanding Number Comparison
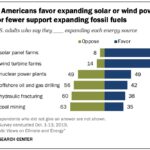
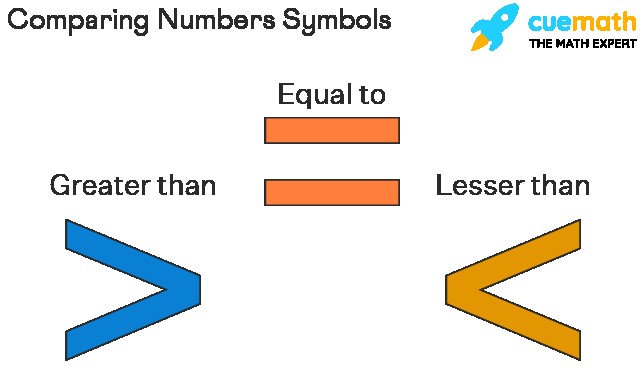
Comparing numbers means determining the relative size of two or more numbers. We use three symbols to represent these comparisons:
- > (Greater than): Indicates that the number on the left is larger than the number on the right (e.g., 5 > 3).
- < (Less than): Indicates that the number on the left is smaller than the number on the right (e.g., 2 < 9).
- = (Equal to): Indicates that both numbers have the same value (e.g., 4 = 4).
Remember, the wider part of the “>” and “<” symbols always faces the larger number, while the pointed end points towards the smaller number.
 comparing numbers symbols
comparing numbers symbols
Steps to Compare Numbers
Comparing numbers involves a straightforward process:
- Digit Count: If the numbers have a different number of digits, the number with more digits is larger.
- Place Value Comparison: If the numbers have the same number of digits, start comparing from the leftmost digit (highest place value).
- Continue Comparing: If the digits in the highest place value are the same, move to the next place value to the right and continue comparing until you find a difference. The number with the larger digit in that place value is the larger number.
Ordering Numbers: Ascending and Descending
Once you can compare numbers, ordering them is simple. There are two ways to order numbers:
- Ascending Order: Arranging numbers from smallest to largest (e.g., 1, 2, 3, 4, 5).
- Descending Order: Arranging numbers from largest to smallest (e.g., 5, 4, 3, 2, 1).
Comparing Rational Numbers
Rational numbers are numbers that can be expressed as a fraction of two integers. Comparing them requires a slightly different approach:
- Find the Least Common Multiple (LCM): Determine the LCM of the denominators of the fractions.
- Create Equivalent Fractions: Convert each fraction to an equivalent fraction with the LCM as the denominator.
- Compare Numerators: Compare the numerators of the equivalent fractions. The fraction with the larger numerator is the larger rational number.
Example: Compare 2/3 and 6/7.
- LCM(3, 7) = 21
- 2/3 = 14/21
- 6/7 = 18/21
Since 18 > 14, then 6/7 > 2/3.
Real-World Applications of Comparing and Ordering Numbers
Comparing and ordering numbers isn’t just a classroom exercise. We use it constantly in everyday life:
- Shopping: Comparing prices to find the best deals.
- Cooking: Measuring ingredients accurately.
- Time Management: Scheduling appointments and tasks.
- Sports: Ranking teams based on performance.
Understanding how to compare and order numbers empowers us to make informed decisions and navigate the world around us effectively.
Conclusion
Comparing and ordering numbers is a crucial foundational skill in mathematics with widespread applications in daily life. By mastering the steps outlined in this article, you can confidently compare and order any set of numbers, from whole numbers to rational numbers. This knowledge will not only enhance your mathematical abilities but also equip you to solve real-world problems efficiently.