How Do We Compare Numbers? Ultimate Guide To Numerical Analysis

How Do We Compare Numbers? This fundamental question is at the heart of mathematics, statistics, and everyday decision-making. COMPARE.EDU.VN offers an exhaustive guide to understanding numerical comparison, providing clarity and actionable insights. Learn how to compare, contrast, and evaluate numbers effectively, leveraging various comparison techniques for enhanced accuracy, comparison metrics, and a better understanding of numerical relationships.

1. Introduction: The Importance of Comparing Numbers

The ability to compare numbers is a cornerstone of logical reasoning and practical problem-solving. Whether you’re a student grappling with mathematical concepts, a consumer evaluating product prices, or a professional analyzing data trends, understanding how to compare numbers is essential. This article, brought to you by COMPARE.EDU.VN, will delve into the various methods and applications of numerical comparison, ensuring you can make informed decisions based on solid quantitative analysis using benchmarking practices and quantifiable data insights.

2. What Does it Mean to Compare Numbers?

Comparing numbers involves determining the relative size or value of two or more numerical quantities. This process allows us to establish relationships such as “greater than,” “less than,” or “equal to” between the numbers, thereby facilitating meaningful comparisons and informed judgments using analytical techniques and evaluative methodologies.

3. Basic Symbols and Terminology

Understanding the basic symbols and terminology is crucial for effective numerical comparison. Here’s a rundown:

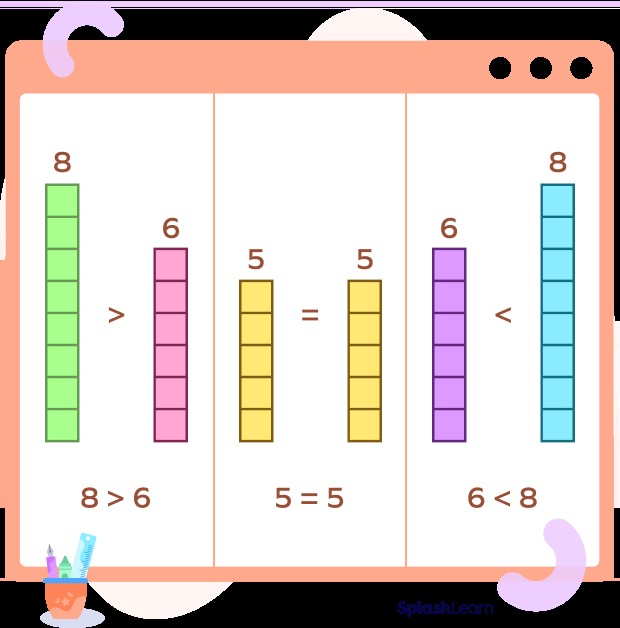
• Greater Than (>): Indicates that one number is larger than another. For example, 5 > 3 means 5 is greater than 3.
• Less Than (<): Indicates that one number is smaller than another. For example, 2 < 7 means 2 is less than 7.
• Equal To (=): Indicates that two numbers have the same value. For example, 4 = 4 means 4 is equal to 4.
• Greater Than or Equal To (≥): Indicates that one number is either larger than or equal to another. For example, x ≥ 5 means x can be 5 or any number greater than 5.
• Less Than or Equal To (≤): Indicates that one number is either smaller than or equal to another. For example, y ≤ 10 means y can be 10 or any number less than 10.
• Not Equal To (≠): Indicates that two numbers do not have the same value. For example, 6 ≠ 8 means 6 is not equal to 8.

These symbols are the building blocks of numerical comparison and are used extensively in mathematical expressions, equations, and inequalities using established mathematical conventions and notational systems.

4. Comparing Whole Numbers

Comparing whole numbers involves several straightforward steps:

4.1. Counting Digits

The first step in comparing whole numbers is to count the number of digits. A number with more digits is always greater.

Example:

• 1,234 (4 digits) vs. 12,345 (5 digits)
• 12,345 is greater than 1,234 because it has more digits.

4.2. Comparing Place Values

If the numbers have the same number of digits, compare the digits from left to right, starting with the highest place value (e.g., thousands, hundreds, tens, ones).

Example:

• 5,678 vs. 5,578
• Both numbers have the same number of digits, so start by comparing the thousands place (5 = 5).
• Next, compare the hundreds place (6 > 5). Therefore, 5,678 is greater than 5,578.

4.3. Handling Identical Digits

If the digits in the highest place values are the same, continue comparing the next digits to the right until you find a difference.

Example:

• 9,876 vs. 9,874
• The thousands, hundreds, and tens places are the same (9, 8, 7).
• Compare the ones place (6 > 4). Therefore, 9,876 is greater than 9,874.

5. Comparing Integers: Positive vs. Negative

Integers include positive numbers, negative numbers, and zero. Comparing integers involves understanding the number line and the concept of negative values using linear scale comparison techniques.

5.1. Positive vs. Negative

Positive integers are always greater than negative integers. Zero is greater than any negative integer but less than any positive integer.

Examples:

• 5 > -3 (positive is greater than negative)
• 0 > -10 (zero is greater than negative)
• 8 > 0 (positive is greater than zero)

5.2. Comparing Positive Integers

Comparing positive integers is the same as comparing whole numbers.

Example:

• 15 > 12

5.3. Comparing Negative Integers

When comparing negative integers, the number closer to zero is greater. This might seem counterintuitive, but consider the number line: -1 is to the right of -5, thus -1 is greater than -5.

Example:

• -2 > -8 (because -2 is closer to zero)
• -1 > -3

6. Comparing Fractions: Making Sense of Parts

Comparing fractions involves understanding the relationship between the numerator (top number) and the denominator (bottom number). There are several methods to compare fractions effectively using fractional valuation methodologies and proportional analysis.

6.1. Like Fractions

Like fractions have the same denominator. To compare like fractions, simply compare the numerators. The fraction with the larger numerator is greater.

Example:

• 3/7 vs. 5/7
• Since 5 > 3, 5/7 > 3/7

6.2. Unlike Fractions

Unlike fractions have different denominators. Here are a few methods to compare them:

6.2.1. Finding a Common Denominator

The most common method is to find a common denominator and convert both fractions to equivalent fractions with that denominator.

Steps:

1. Find the Least Common Multiple (LCM) of the denominators.
2. Convert each fraction to an equivalent fraction with the LCM as the denominator.
3. Compare the numerators.

Example:

• 1/3 vs. 2/5

  1. LCM of 3 and 5 is 15.
  2. Convert the fractions:
     • 1/3 = (1 5) / (3 5) = 5/15
     • 2/5 = (2 3) / (5 3) = 6/15
  3. Compare the numerators:
     • Since 6 > 5, 6/15 > 5/15, so 2/5 > 1/3

6.2.2. Cross-Multiplication

Cross-multiplication is a quick method to compare two fractions.

Steps:

1. Multiply the numerator of the first fraction by the denominator of the second fraction.
2. Multiply the numerator of the second fraction by the denominator of the first fraction.
3. Compare the results.

Example:

• 3/4 vs. 5/7

  1. *3 7 = 21**
  2. *5 4 = 20**
  3. Compare the results:
     • Since 21 > 20, 3/4 > 5/7

6.2.3. Converting to Decimals

Another method is to convert each fraction to a decimal and then compare the decimals.

Example:

• 1/4 vs. 3/10

  1. Convert the fractions:
     • 1/4 = 0.25
     • 3/10 = 0.3
  2. Compare the decimals:
     • Since 0.3 > 0.25, 3/10 > 1/4

7. Comparing Decimals: Precision Matters

Comparing decimals involves comparing the digits in each place value, similar to comparing whole numbers. Decimal place valuation and significant digit analysis are critical components of this process.

7.1. Aligning Decimal Points

The first step is to align the decimal points and add trailing zeros so that both numbers have the same number of decimal places.

Example:

• 2.35 vs. 2.3

  • Align the decimal points and add a trailing zero to 2.3:
    • 2.35 vs. 2.30

7.2. Comparing Place Values

Start by comparing the whole number part. If they are the same, compare the digits to the right of the decimal point, one place value at a time.

Example:

• 4.56 vs. 4.58

  • The whole number parts are the same (4 = 4).
  • The tenths place is the same (5 = 5).
  • Compare the hundredths place (6 < 8). Therefore, 4.56 < 4.58.

7.3. Dealing with Repeating Decimals

When dealing with repeating decimals, it’s often best to convert them to fractions or compare them to a sufficient number of decimal places to observe a pattern.

Example:

• 0.333… vs. 0.33

  • 0. 333… is greater than 0.33 because the repeating 3s continue indefinitely, making it slightly larger.

8. Comparing Rational Numbers

Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers and q ≠ 0. Comparing rational numbers is similar to comparing fractions, but you also need to consider the sign of the numbers. Rational number line analysis and fractional equivalent assessments are essential tools for accurate comparisons.

8.1. Positive vs. Negative

As with integers, positive rational numbers are always greater than negative rational numbers.

Example:

• 1/2 > -1/4

8.2. Comparing Positive Rational Numbers

Use the methods for comparing fractions.

Example:

• 2/3 vs. 3/4

  • Using cross-multiplication:
    • 2 * 4 = 8
    • 3 * 3 = 9
    • Since 9 > 8, 3/4 > 2/3

8.3. Comparing Negative Rational Numbers

When comparing negative rational numbers, the number closer to zero is greater.

Example:

• -1/3 vs. -1/2

  • Find a common denominator:
    • -1/3 = -2/6
    • -1/2 = -3/6
  • Since -2/6 is closer to zero, -1/3 > -1/2

9. Comparing Irrational Numbers

Irrational numbers cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal representations (e.g., √2, π). Comparing irrational numbers often involves approximation or using known properties. Irrational number approximation and numerical estimation techniques are key here.

9.1. Using Approximations

Approximate the irrational numbers to a few decimal places and then compare.

Example:

• √2 vs. 1.4

  • √2 ≈ 1.414
  • Since 1.414 > 1.4, √2 > 1.4

9.2. Using Known Properties

Use known properties of the numbers. For example, if you know that π ≈ 3.14159, you can compare it to other numbers.

Example:

• π vs. 3.14

  • Since π ≈ 3.14159, π > 3.14

9.3. Squaring (for Square Roots)

If comparing square roots, you can square both numbers and then compare the results.

Example:

• √5 vs. 2

  • (√5)² = 5
  • 2² = 4
  • Since 5 > 4, √5 > 2

10. Comparing Numbers in Scientific Notation

Scientific notation is a way to express very large or very small numbers as a product of a number between 1 and 10 and a power of 10 (e.g., 3.2 x 10^5). Comparing numbers in scientific notation involves comparing the exponents and the coefficients using exponential and coefficient analysis.

10.1. Comparing Exponents

If the exponents are different, the number with the larger exponent is greater.

Example:

• 3. 5 x 10^6 vs. 2.1 x 10^5
  • Since 6 > 5, 3.5 x 10^6 > 2.1 x 10^5

10.2. Comparing Coefficients

If the exponents are the same, compare the coefficients.

Example:

• 4. 2 x 10^8 vs. 3.9 x 10^8
  • The exponents are the same (8 = 8).
  • Since 4.2 > 3.9, 4.2 x 10^8 > 3.9 x 10^8

11. Real-Life Applications of Comparing Numbers

Comparing numbers is a fundamental skill used in numerous real-life situations. Here are a few examples where numerical comparison is essential for informed decision-making and critical thinking:

11.1. Personal Finance

• Budgeting: Comparing income and expenses to manage finances effectively.
• Shopping: Comparing prices of products to find the best deals.
• Investments: Evaluating returns on different investment options.
• Loans: Comparing interest rates on loans to minimize costs.

Example:

• Comparing the price of a laptop at two different stores:
  • Store A: $800
  • Store B: $750
  • Decision: Buy from Store B because $750 < $800.

11.2. Health and Fitness

• Nutrition: Comparing calorie counts of different foods.
• Exercise: Comparing distances run or weights lifted over time to track progress.
• Medical Data: Comparing blood pressure readings or cholesterol levels to assess health.

Example:

• Comparing the calorie count of two snacks:
  • Snack A: 250 calories
  • Snack B: 150 calories
  • Decision: Choose Snack B because 150 < 250 for a lower calorie intake.

11.3. Cooking and Baking

• Recipes: Comparing ingredient amounts to scale recipes up or down.
• Cooking Times: Adjusting cooking times based on oven temperature.

Example:

• Scaling a recipe that calls for 1/2 cup of flour to double the recipe:
  • Original: 1/2 cup
  • Doubled: 1/2 * 2 = 1 cup
  • Adjustment: Use 1 cup of flour.

11.4. Travel and Navigation

• Distance: Comparing distances between locations to plan routes.
• Time: Comparing travel times using different modes of transportation.
• Costs: Comparing the prices of flights, hotels, and rental cars.

Example:

• Comparing the distance between two cities using different routes:
  • Route A: 350 miles
  • Route B: 320 miles
  • Decision: Choose Route B because 320 < 350 for a shorter distance.

11.5. Business and Marketing

• Sales Data: Comparing sales figures over different periods to identify trends.
• Market Analysis: Comparing market share of different companies.
• Performance Metrics: Comparing key performance indicators (KPIs) to assess business performance.

Example:

• Comparing the sales revenue of two quarters:
  • Q1: $500,000
  • Q2: $550,000
  • Analysis: Sales increased in Q2 because $550,000 > $500,000.

11.6. Science and Engineering

• Measurements: Comparing measurements in experiments to analyze results.
• Data Analysis: Comparing data sets to identify patterns and draw conclusions.
• Performance Metrics: Comparing the performance of different designs or systems.

Example:

• Comparing the efficiency of two solar panels:
  • Panel A: 18% efficiency
  • Panel B: 20% efficiency
  • Analysis: Panel B is more efficient because 20% > 18%.

12. Common Mistakes to Avoid

When comparing numbers, it’s easy to make mistakes that can lead to incorrect conclusions. Here are some common pitfalls to avoid:

12.1. Not Ensuring Units are Consistent

Always make sure that the numbers you are comparing are in the same units.

Example:

• Incorrect: Comparing 5 meters to 50 centimeters without converting.
• Correct: Convert 5 meters to 500 centimeters and then compare 500 cm to 50 cm.

12.2. Ignoring Negative Signs

Remember that negative numbers behave differently than positive numbers.

Example:

• Incorrect: Thinking -5 is greater than -2.
• Correct: -2 is greater than -5 because it is closer to zero.

12.3. Not Considering Context

Always consider the context in which the numbers are being compared.

Example:

• A 10% increase in a small number might be insignificant compared to a 5% increase in a large number.

12.4. Rounding Errors

Be careful when rounding numbers, as this can introduce errors in your comparisons.

Example:

• Rounding 3.14159 to 3.14 might lead to incorrect conclusions if comparing it to a number very close to 3.14.

12.5. Not Using Appropriate Tools

Use calculators, spreadsheets, or other tools to help with complex comparisons and avoid manual calculation errors.

13. Advanced Techniques in Numerical Comparison

For more complex scenarios, advanced techniques can provide deeper insights into numerical relationships:

13.1. Statistical Analysis

Statistical methods such as t-tests, ANOVA, and regression analysis can be used to compare groups of numbers and determine if differences are statistically significant.

13.2. Indexing and Normalization

Indexing and normalization techniques can be used to compare numbers that are on different scales, making it easier to identify trends and patterns.

13.3. Visualization

Visualizing data through charts and graphs can help to identify patterns and relationships that might not be apparent when looking at raw numbers.

14. How COMPARE.EDU.VN Can Help

At COMPARE.EDU.VN, we understand the challenges of making informed decisions in a world filled with complex data. That’s why we provide comprehensive comparison tools and resources to help you evaluate different options objectively and efficiently. Whether you’re comparing products, services, or ideas, our platform offers detailed analyses and user-friendly interfaces to simplify the decision-making process.

14.1. Detailed Comparison Articles

COMPARE.EDU.VN offers a wide range of articles comparing various topics, from technology and finance to health and education. These articles provide in-depth analysis and objective evaluations to help you make informed decisions.

14.2. User-Friendly Tools

Our platform features user-friendly tools that allow you to compare different options side-by-side. These tools provide a clear and concise overview of the key differences between the options, making it easy to identify the best choice for your needs.

14.3. Expert Reviews

COMPARE.EDU.VN features expert reviews from industry professionals who provide valuable insights and recommendations. These reviews can help you to better understand the strengths and weaknesses of different options, allowing you to make a more informed decision.

14.4. Community Feedback

Our platform allows users to share their experiences and opinions, providing a valuable source of feedback and insights. This community-driven approach ensures that you have access to a wide range of perspectives, helping you to make the best possible decision.

15. Conclusion: Making Informed Decisions

Comparing numbers is a fundamental skill that is essential for making informed decisions in all aspects of life. By understanding the basic principles and techniques of numerical comparison, you can evaluate different options objectively and efficiently, ensuring that you make the best possible choices. Visit COMPARE.EDU.VN today to discover how our comprehensive comparison tools and resources can help you navigate the complexities of the modern world and make informed decisions with confidence using data analysis methods and comparative decision-making.

Remember, whether you’re a student, a consumer, or a professional, the ability to compare numbers effectively is a valuable asset that will serve you well throughout your life. Let COMPARE.EDU.VN be your trusted partner in this journey, providing you with the tools and resources you need to succeed and foster quantitative literacy.

16. Call to Action

Ready to make smarter decisions? Visit COMPARE.EDU.VN today to explore our comprehensive comparison tools and resources. Whether you’re comparing gadgets, financial products, educational courses, or anything else, COMPARE.EDU.VN is your go-to source for objective, detailed comparisons. Don’t make another decision without consulting our expert analyses.

For further assistance, contact us at:
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
WhatsApp: +1 (626) 555-9090
Website: COMPARE.EDU.VN

17. FAQs About Comparing Numbers

1. What is the first step in comparing whole numbers?

• The first step is to count the number of digits. The number with more digits is greater.

2. How do you compare fractions with different denominators?

• You can find a common denominator, cross-multiply, or convert the fractions to decimals.

3. What is the rule for comparing negative integers?

• The negative integer closer to zero is greater. For example, -2 is greater than -5.

4. How do you compare numbers in scientific notation?

• First, compare the exponents. If the exponents are the same, compare the coefficients.

5. Why is it important to ensure units are consistent when comparing numbers?

• Inconsistent units can lead to incorrect comparisons. Always convert numbers to the same units before comparing.

6. What is cross-multiplication, and how is it used to compare fractions?

• Cross-multiplication involves multiplying the numerator of one fraction by the denominator of the other. Comparing the results helps determine which fraction is greater.

7. How can COMPARE.EDU.VN help me compare different products or services?

• compare.edu.vn provides detailed comparison articles, user-friendly tools, expert reviews, and community feedback to help you make informed decisions.

8. What is the significance of place value when comparing decimals?

• Place value determines the magnitude of each digit. Comparing digits in the same place value (tenths, hundredths, etc.) is crucial for accurate decimal comparisons.

9. How do you compare irrational numbers like √2 and π?

• You can approximate irrational numbers to a few decimal places or use known properties to compare them.

10. What are some common mistakes to avoid when comparing numbers?

• Common mistakes include not ensuring consistent units, ignoring negative signs, not considering context, and rounding errors.