How Do Mean And Median Compare? This is a fundamental question in statistics that COMPARE.EDU.VN addresses, offering clarity on these measures of central tendency and their applications. Understanding the nuances between the mean (average) and the median (middle value) is crucial for accurate data analysis and informed decision-making. Dive into a detailed comparison of the mean and median, exploring their strengths, weaknesses, and the scenarios where each is most effective. We’ll explore central tendency measures, data distribution insights, and robust statistical analysis.
1. Understanding Mean and Median
The mean and median are two key measures of central tendency in statistics, each providing a different perspective on the “average” value within a dataset. Understanding their distinct characteristics is essential for effective data analysis.
1.1. What is the Mean?
The mean, often referred to as the average, is calculated by summing all the values in a dataset and dividing by the total number of values. It’s a widely used measure that provides a sense of the typical value in a dataset.
Formula:
Mean (μ) = (Σxᵢ) / n
Where:
- Σxᵢ represents the sum of all values in the dataset.
- n is the number of values in the dataset.
Example:
Consider the dataset: 2, 4, 6, 8, 10
Mean = (2 + 4 + 6 + 8 + 10) / 5 = 30 / 5 = 6
1.2. What is the Median?
The median is the middle value in a dataset when the values are arranged in ascending or descending order. It divides the dataset into two equal halves, with 50% of the values falling below the median and 50% above it.
Finding the Median:
- Arrange the data: Sort the dataset in ascending order.
- Odd number of values: If the dataset contains an odd number of values, the median is the middle value.
- Even number of values: If the dataset contains an even number of values, the median is the average of the two middle values.
Example 1 (Odd Number of Values):
Consider the dataset: 2, 4, 6, 8, 10
Median = 6 (the middle value)
Example 2 (Even Number of Values):
Consider the dataset: 2, 4, 6, 8
Median = (4 + 6) / 2 = 5 (the average of the two middle values)
1.3. Key Differences Between Mean and Median
| Feature | Mean | Median |
|---|---|---|
| Calculation | Sum of all values divided by the number of values. | Middle value when data is sorted. |
| Sensitivity to Outliers | Highly sensitive; outliers can significantly affect the mean. | Robust; less affected by outliers. |
| Use Cases | Suitable for datasets with symmetrical distributions and no extreme outliers. | Suitable for datasets with skewed distributions or when outliers are present. |
| Interpretation | Represents the “average” value in the dataset. | Represents the “middle” value, dividing the dataset into two equal halves. |
| Mathematical Properties | The mean minimizes the sum of squared deviations. | The median minimizes the sum of absolute deviations. |
| Data Requirement | Requires numerical data. | Requires ordinal or numerical data. |
1.4. Visual Representation
To further illustrate the difference, consider a dataset represented as a histogram. The mean is the point where the histogram would balance if it were a physical object, while the median is the point that divides the area of the histogram into two equal parts.
Alt Text: Histogram visually comparing the mean and median in a data distribution, showcasing their positions relative to the data’s central tendency and skewness.
Understanding these fundamental differences sets the stage for a deeper exploration of when to use each measure and how they perform under different conditions. At COMPARE.EDU.VN, we provide comprehensive comparisons and analyses to help you make informed decisions based on your data.
2. Sensitivity to Outliers
One of the most significant differences between the mean and median lies in their sensitivity to outliers. Outliers are extreme values in a dataset that deviate significantly from other values. Understanding how these measures react to outliers is crucial in selecting the appropriate measure of central tendency.
2.1. How Outliers Affect the Mean
The mean is highly sensitive to outliers because it takes into account every value in the dataset. When an outlier is present, it can disproportionately influence the sum of the values, leading to a mean that doesn’t accurately represent the typical value.
Example:
Consider the dataset: 10, 12, 14, 16, 18
Mean = (10 + 12 + 14 + 16 + 18) / 5 = 70 / 5 = 14
Now, let’s introduce an outlier: 10, 12, 14, 16, 100
Mean = (10 + 12 + 14 + 16 + 100) / 5 = 152 / 5 = 30.4
In this case, the outlier (100) significantly increased the mean from 14 to 30.4, which no longer accurately represents the central tendency of the original data.
2.2. How Outliers Affect the Median
The median is robust to outliers because it only considers the middle value(s) in the dataset. Outliers do not affect the median unless they are so extreme that they change the order of the middle values.
Example:
Consider the dataset: 10, 12, 14, 16, 18
Median = 14
Now, let’s introduce an outlier: 10, 12, 14, 16, 100
Median = 14
In this case, the outlier (100) did not change the median at all. The median remains 14, providing a more accurate representation of the central tendency of the data.
2.3. Why the Median is More Robust
The median’s robustness stems from its definition as the point that divides the dataset into two equal halves. Outliers can only affect the median if they cross this dividing point, which requires a substantial number of extreme values.
Mathematical Explanation:
The mean minimizes the sum of squared deviations, making it sensitive to large deviations caused by outliers. The median, on the other hand, minimizes the sum of absolute deviations, which is less sensitive to extreme values.
2.4. Real-World Examples
Income Data:
In income data, outliers (extremely high incomes) can significantly inflate the mean income, making it appear higher than what most people earn. The median income, which is less affected by these outliers, provides a more accurate representation of the typical income.
Housing Prices:
Similarly, in housing price data, a few very expensive properties can skew the mean price upwards. The median house price gives a better sense of the “middle” price point, unaffected by these high-end outliers.
2.5. Visualizing the Impact of Outliers
Consider a box plot, which displays the median, quartiles, and outliers in a dataset. The box represents the interquartile range (IQR), and the median is shown as a line within the box. Outliers are plotted as individual points outside the whiskers.
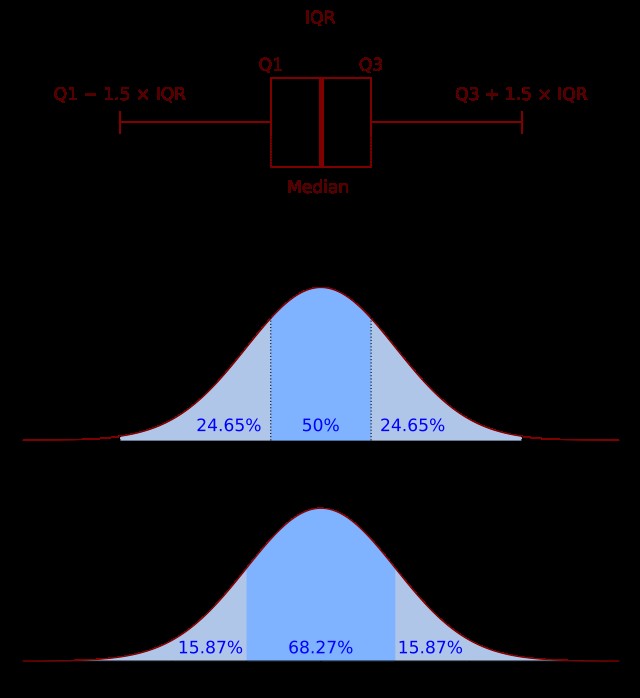Box plot illustrating the impact of outliers on mean and median
Alt Text: Box plot comparing how outliers influence the mean and median, highlighting the median’s stability and the mean’s susceptibility to extreme values.
The box plot visually demonstrates how outliers can skew the mean, while the median remains relatively stable within the box.
Understanding the impact of outliers is crucial for selecting the appropriate measure of central tendency. At COMPARE.EDU.VN, we emphasize the importance of considering data distribution and potential outliers when comparing different datasets or making statistical inferences.
3. Data Distribution and Skewness
The shape of a dataset’s distribution plays a crucial role in determining whether the mean or median is a more appropriate measure of central tendency. Skewness, in particular, can significantly influence the relationship between the mean and median.
3.1. Symmetrical Distribution
In a symmetrical distribution, the data is evenly distributed around the center. This means that the left and right sides of the distribution are mirror images of each other.
Characteristics:
- Mean = Median = Mode (in a perfectly symmetrical distribution)
- Data is balanced, with no skewness.
Example:
A normal distribution (bell curve) is a classic example of a symmetrical distribution.
Alt Text: Normal distribution graph showcasing perfect symmetry around the mean, median, and mode, all coinciding at the center of the curve.
In a symmetrical distribution, the mean and median are equal and both provide an accurate representation of the central tendency.
3.2. Skewed Distribution
A skewed distribution is asymmetrical, with one tail longer than the other. Skewness indicates the direction and extent to which the data is not evenly distributed.
Types of Skewness:
- Positive Skew (Right Skew): The tail is longer on the right side, indicating that there are some high values pulling the mean to the right.
- Negative Skew (Left Skew): The tail is longer on the left side, indicating that there are some low values pulling the mean to the left.
Positive Skew:
- Mean > Median
- The mean is pulled towards the longer tail, making it higher than the median.
Negative Skew:
- Mean < Median
- The mean is pulled towards the longer tail, making it lower than the median.
Examples:
- Positive Skew: Income distribution (where a few high earners skew the mean upwards)
- Negative Skew: Age at death (where most people live to an older age, but some die young)
3.3. Visualizing Skewness
Histograms and density plots are useful tools for visualizing skewness. In a positively skewed distribution, the histogram will have a long tail on the right, while in a negatively skewed distribution, the histogram will have a long tail on the left.
Positive Skew:
Alt Text: Graph of a positively skewed distribution showing the long tail extending to the right, indicating that the mean is greater than the median.
Negative Skew:
Alt Text: Graph of a negatively skewed distribution showing the long tail extending to the left, indicating that the mean is less than the median.
3.4. Choosing Between Mean and Median in Skewed Distributions
In skewed distributions, the median is generally a better measure of central tendency because it is less affected by the extreme values in the longer tail. The mean can be misleading as it is pulled towards the tail, misrepresenting the typical value.
Guidelines:
- Symmetrical Distribution: Both mean and median are suitable.
- Positive Skew: Median is preferred.
- Negative Skew: Median is preferred.
3.5. Real-World Implications
Real Estate:
When analyzing housing prices in a neighborhood with a few very expensive homes, the median price is a more representative measure of what a typical home costs compared to the mean price, which can be inflated by the high-end properties.
Healthcare:
In healthcare, analyzing the length of hospital stays, the median length of stay is often used because the distribution can be skewed by a few patients with very long stays.
At COMPARE.EDU.VN, we provide tools and resources to analyze data distributions and help you choose the most appropriate measure of central tendency for your specific needs. Understanding skewness and its impact on the mean and median is essential for accurate data interpretation and decision-making.
4. Applications in Different Fields
The mean and median are used extensively across various fields, each offering unique insights depending on the context. Understanding their specific applications can help in making informed decisions and drawing accurate conclusions.
4.1. Finance
In finance, both the mean and median play crucial roles in analyzing financial data, but they are used in different contexts.
Mean:
- Average Return: The mean is used to calculate the average return on an investment over a period of time.
- Portfolio Performance: It helps in assessing the overall performance of a portfolio by averaging the returns of individual assets.
Median:
- Income Analysis: The median income is a more reliable measure of typical income than the mean, as it is less affected by extremely high incomes.
- Housing Prices: The median home price provides a better representation of the typical home value in a specific area.
Example:
Consider a hedge fund that has the following annual returns over 10 years: 5%, 8%, 10%, 12%, 6%, 7%, 9%, 11%, 5%, 50% (due to a lucky investment).
Mean Return = (5 + 8 + 10 + 12 + 6 + 7 + 9 + 11 + 5 + 50) / 10 = 12.3%
Median Return = (7 + 8) / 2 = 7.5%
In this case, the mean return is significantly inflated by the outlier (50%), while the median return gives a more accurate picture of the fund’s typical performance.
4.2. Healthcare
In healthcare, the mean and median are used to analyze patient data, treatment outcomes, and healthcare costs.
Mean:
- Average Length of Stay: The mean length of stay in a hospital is used for resource allocation and capacity planning.
- Average Treatment Cost: The mean cost of a particular treatment is used for budgeting and cost analysis.
Median:
- Median Survival Time: In clinical trials, the median survival time is a more robust measure than the mean, as it is less affected by a few patients who live significantly longer or shorter than others.
- Median Time to Recovery: It provides a better understanding of the typical recovery time for a specific condition.
Example:
Consider a study on the survival time of patients with a particular type of cancer. The survival times in months are: 12, 15, 18, 20, 22, 25, 28, 30, 35, 60 (one patient lived much longer).
Mean Survival Time = (12 + 15 + 18 + 20 + 22 + 25 + 28 + 30 + 35 + 60) / 10 = 26.5 months
Median Survival Time = (22 + 25) / 2 = 23.5 months
The median survival time is less influenced by the outlier (60 months) and gives a more accurate representation of the typical survival time.
4.3. Education
In education, the mean and median are used to analyze student performance, test scores, and educational outcomes.
Mean:
- Grade Point Average (GPA): The mean GPA is used to assess a student’s overall academic performance.
- Average Test Score: The mean test score is used to evaluate the performance of a class or school.
Median:
- Median Test Score: The median test score is a better measure of the typical performance of students, especially when there are outliers (very high or very low scores).
- Median Years of Education: It provides insights into the educational attainment of a population.
Example:
Consider a class with the following test scores: 60, 70, 75, 80, 85, 90, 92, 95, 98, 100.
Mean Score = (60 + 70 + 75 + 80 + 85 + 90 + 92 + 95 + 98 + 100) / 10 = 84.5
Median Score = (85 + 90) / 2 = 87.5
In this case, both the mean and median provide similar information, but if there were a few very low scores, the median would be a more robust measure.
4.4. Environmental Science
In environmental science, the mean and median are used to analyze environmental data, pollution levels, and climate trends.
Mean:
- Average Temperature: The mean temperature is used to track climate change and temperature trends.
- Average Rainfall: The mean rainfall is used to monitor precipitation patterns.
Median:
- Median Pollution Level: The median pollution level is a more reliable measure of typical pollution, especially when there are spikes in pollution levels due to specific events.
- Median Water Quality Index: It provides a better understanding of the typical water quality in a specific area.
Example:
Consider a study monitoring air pollution levels in a city. The pollution levels (in parts per million) over 10 days are: 5, 7, 6, 8, 9, 5, 6, 7, 8, 50 (one day with very high pollution).
Mean Pollution Level = (5 + 7 + 6 + 8 + 9 + 5 + 6 + 7 + 8 + 50) / 10 = 11.1 ppm
Median Pollution Level = (7 + 7) / 2 = 7 ppm
The median pollution level is less influenced by the outlier (50 ppm) and gives a more accurate representation of the typical air quality.
4.5. Marketing
In marketing, the mean and median are used to analyze customer data, sales figures, and marketing campaign performance.
Mean:
- Average Purchase Value: The mean purchase value is used to understand the typical amount customers spend per transaction.
- Average Customer Lifetime Value: It helps in assessing the long-term value of a customer.
Median:
- Median Purchase Value: The median purchase value provides a better understanding of the typical transaction amount, especially when there are a few very large purchases.
- Median Customer Acquisition Cost: It gives a more accurate representation of the typical cost to acquire a customer.
Example:
Consider a retail store analyzing customer purchase values. The purchase values of 10 customers are: $20, $25, $30, $35, $40, $45, $50, $55, $60, $200 (one customer made a very large purchase).
Mean Purchase Value = (20 + 25 + 30 + 35 + 40 + 45 + 50 + 55 + 60 + 200) / 10 = $56
Median Purchase Value = (40 + 45) / 2 = $42.50
The median purchase value is less influenced by the outlier ($200) and gives a more accurate representation of the typical customer spending.
At COMPARE.EDU.VN, we provide detailed comparisons and analyses across various fields, helping you understand the most appropriate use of the mean and median for your specific applications.
5. Advantages and Disadvantages
Both the mean and median have their strengths and weaknesses, making them suitable for different types of data and analytical purposes.
5.1. Advantages of the Mean
- Simplicity: The mean is easy to calculate and understand.
- Familiarity: It is the most commonly used measure of central tendency, making it widely accepted and understood.
- Mathematical Properties: The mean has desirable mathematical properties, such as minimizing the sum of squared deviations.
- Use of All Data: The mean takes into account every value in the dataset, providing a comprehensive measure of central tendency.
5.2. Disadvantages of the Mean
- Sensitivity to Outliers: The mean is highly affected by outliers, which can distort the representation of the typical value.
- Misleading in Skewed Distributions: In skewed distributions, the mean can be misleading as it is pulled towards the longer tail.
- Requires Interval or Ratio Data: The mean is only appropriate for interval or ratio data, where the differences between values are meaningful.
5.3. Advantages of the Median
- Robustness to Outliers: The median is not significantly affected by outliers, making it a more reliable measure in datasets with extreme values.
- Suitable for Skewed Distributions: In skewed distributions, the median provides a more accurate representation of the central tendency.
- Requires Ordinal, Interval, or Ratio Data: The median can be used with ordinal data, where the values can be ranked but the differences are not necessarily meaningful.
- Intuitive Interpretation: The median is easy to interpret as the middle value in the dataset.
5.4. Disadvantages of the Median
- Ignores Some Data: The median only considers the middle value(s) and ignores the rest of the data, potentially losing some information.
- Less Mathematical Utility: The median has fewer desirable mathematical properties compared to the mean.
- Less Familiar: Although widely used, the median is not as universally understood as the mean.
5.5. Summary Table
| Feature | Mean | Median |
|---|---|---|
| Advantages | Simple, familiar, uses all data | Robust to outliers, suitable for skewed data |
| Disadvantages | Sensitive to outliers, misleading in skewness | Ignores some data, less mathematical utility |
| Data Type Requirement | Interval or ratio | Ordinal, interval, or ratio |
5.6. When to Use Each Measure
- Use the Mean when:
- The data is symmetrically distributed.
- There are no significant outliers.
- You need to use all the data in the calculation.
- Use the Median when:
- The data is skewed.
- There are significant outliers.
- You need a robust measure of central tendency.
At COMPARE.EDU.VN, we provide tools and resources to help you weigh the advantages and disadvantages of each measure and choose the most appropriate one for your specific analytical needs.
6. Combined Use of Mean and Median
In some cases, using both the mean and median can provide a more comprehensive understanding of the data.
6.1. Detecting Skewness
Comparing the mean and median can help detect skewness in the data.
- Mean ≈ Median: Indicates a symmetrical distribution.
- Mean > Median: Indicates a positive skew.
- Mean < Median: Indicates a negative skew.
By examining the difference between the mean and median, you can gain insights into the shape of the distribution and the presence of outliers.
6.2. Identifying Outliers
When the mean and median are significantly different, it suggests the presence of outliers. The median provides a more robust measure of central tendency in this case, while the mean can be used to quantify the impact of the outliers.
6.3. Complementary Analysis
Using both measures can provide a more nuanced understanding of the data. For example, in income analysis, the median income gives a sense of the typical income, while the mean income can indicate the overall wealth distribution.
6.4. Example: Analyzing Sales Data
Consider a retail store analyzing daily sales data. They calculate both the mean and median daily sales.
- Mean Daily Sales: $1,500
- Median Daily Sales: $1,200
The difference between the mean and median suggests that there are some days with significantly higher sales, pulling the mean upwards. Further investigation reveals that these higher sales days are typically associated with promotional events.
By using both the mean and median, the store can gain a better understanding of their sales patterns and the impact of promotional events.
6.5. Graphical Representation
Using histograms and box plots can visually represent both the mean and median, providing a clear picture of the data distribution and the relationship between the two measures.
Alt Text: Combined histogram and box plot displaying the distribution of data along with the mean and median, highlighting skewness and outliers.
At COMPARE.EDU.VN, we emphasize the importance of using multiple measures and graphical representations to gain a comprehensive understanding of the data. Combining the mean and median can provide valuable insights that would not be apparent from using either measure alone.
7. Advanced Concepts and Considerations
Beyond the basic understanding of mean and median, there are several advanced concepts and considerations that can enhance your data analysis skills.
7.1. Trimmed Mean
A trimmed mean is a compromise between the mean and median. It involves calculating the mean after removing a certain percentage of the extreme values from both ends of the dataset.
Advantages:
- Reduces the impact of outliers while still using most of the data.
- Provides a more robust measure of central tendency than the standard mean.
Example:
A 10% trimmed mean involves removing the highest and lowest 10% of the values before calculating the mean.
7.2. Weighted Mean
A weighted mean assigns different weights to different values in the dataset. This is useful when some values are more important or representative than others.
Formula:
Weighted Mean = (Σ(wᵢ * xᵢ)) / Σwᵢ
Where:
- wᵢ is the weight assigned to the i-th value.
- xᵢ is the i-th value.
Example:
In a course, assignments might be weighted more heavily than quizzes. The weighted mean would reflect this difference in importance.
7.3. Geometric Mean
The geometric mean is used to calculate the average rate of change over time. It is particularly useful in finance for calculating average investment returns.
Formula:
Geometric Mean = (x₁ x₂ … * xₙ)^(1/n)
Example:
If an investment has returns of 10%, 20%, and -5% over three years, the geometric mean return is:
Geometric Mean = (1.10 1.20 0.95)^(1/3) – 1 ≈ 0.077 or 7.7%
7.4. Harmonic Mean
The harmonic mean is used to calculate the average rate when the rates are expressed in different units. It is particularly useful in physics and finance.
Formula:
Harmonic Mean = n / (Σ(1/xᵢ))
Example:
If a car travels 100 miles at 50 mph and then returns at 60 mph, the harmonic mean speed is:
Harmonic Mean = 2 / (1/50 + 1/60) ≈ 54.55 mph
7.5. Population vs. Sample
It’s important to distinguish between the population mean and the sample mean.
- Population Mean (μ): The mean of all values in the entire population.
- Sample Mean (x̄): The mean of a subset of values from the population.
The sample mean is used to estimate the population mean, and the accuracy of the estimate depends on the size and representativeness of the sample.
7.6. Considerations for Data Quality
The accuracy of the mean and median depends on the quality of the data. It’s important to address issues such as:
- Missing Values: Impute or remove missing values appropriately.
- Measurement Errors: Correct or account for measurement errors.
- Data Integrity: Ensure the data is accurate and consistent.
At COMPARE.EDU.VN, we provide resources and tools to help you address these advanced concepts and considerations, ensuring that your data analysis is accurate and reliable.
8. Practical Examples and Case Studies
To further illustrate the concepts discussed, let’s explore some practical examples and case studies.
8.1. Case Study: Analyzing Customer Satisfaction Scores
A company collects customer satisfaction scores on a scale of 1 to 10. The scores from 100 customers are as follows:
[7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 7, 8, 9, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 1, 2]
Analysis:
- Mean: 7.25
- Median: 8
- Distribution: The distribution is skewed to the left due to a few very low scores.
Interpretation:
The median customer satisfaction score of 8 provides a more accurate representation of the typical satisfaction level than the mean of 7.25, which is pulled down by the low scores.
8.2. Example: Comparing Salaries in Two Departments
A company wants to compare the salaries in two departments: Sales and Marketing. The salaries (in thousands of dollars) are as follows:
- Sales: [50, 60, 70, 80, 90, 100, 110, 120, 130, 500]
- Marketing: [60, 65, 70, 75, 80, 85, 90, 95, 100, 105]
Analysis:
- Sales Mean: 131
- Sales Median: 95
- Marketing Mean: 82.5
- Marketing Median: 82.5
Interpretation:
In the Sales department, the mean salary is significantly higher than the median due to an outlier (one employee earning $500,000). The median salary of $95,000 provides a more accurate representation of the typical salary in the Sales department. In the Marketing department, the mean and median salaries are the same, indicating a symmetrical distribution.
8.3. Example: Analyzing Website Load Times
A website owner wants to analyze the load times of their website pages. They collect the load times (in seconds) for 100 page views.
Analysis:
After analyzing the data, they find that the distribution of load times is skewed to the right, with a few pages taking significantly longer to load.
Recommendations:
They should use the median load time as a key metric for monitoring website performance. They should also investigate the pages with the longest load times to identify and address any performance issues.
8.4. Example: Comparing Test Scores in Two Schools
Two schools administer the same standardized test. The test scores are as follows:
- School A: [70, 75, 80, 85, 90, 95, 100, 105, 110, 115]
- School B: [60, 65, 70, 75, 80, 85, 90, 95, 100, 200]
Analysis:
- School A Mean: 92.5
- School A Median: 92.5
- School B Mean: 92
- School B Median: 82.5
Interpretation:
In School A, the mean and median test scores are the same, indicating a symmetrical distribution. In School B, the mean test score is higher than the median due to an outlier (one student scoring 200). The median test score of 82.5 provides a more accurate representation of the typical performance in School B.
At COMPARE.EDU.VN, we provide tools and resources to help you analyze real-world data and make informed decisions based on your findings. These practical examples and case studies demonstrate the importance of understanding the mean and median and how to use them effectively.
9. Conclusion: Choosing the Right Measure
Selecting the appropriate measure of central tendency—mean or median—hinges on understanding the data’s distribution and the potential influence of outliers. The mean, while simple and widely used, is susceptible to distortion by extreme values, making it less reliable for skewed datasets. Conversely, the median offers robustness against outliers, providing a more accurate representation of central tendency in such cases.
9.1. Key Takeaways
- Mean: Use for symmetrical data without significant outliers.
- Median: Use for skewed data or when outliers are present.
- Combined Use: Comparing mean and median can reveal skewness and outliers.
- Advanced Concepts: Trimmed mean, weighted mean, geometric mean, and harmonic mean offer additional analytical options.
- Data Quality: Ensure data accuracy by addressing missing values and measurement errors.
9.2. Importance of Data Context
The choice between mean and median should always be informed by the context of the data and the specific analytical goals. Consider the nature of the data, the potential for outliers, and the desired level of robustness when making your decision.
9.3. Limitations and Further Analysis
While the mean and median are valuable measures of central tendency, they provide only a partial view of the data. It’s important to supplement these measures with other statistical tools, such as standard deviation, variance, and graphical representations, to gain a more comprehensive understanding.
9.4. The Role of COMPARE.EDU.VN
At compare.edu.vn, we are committed to providing you with the resources and tools you need to make informed decisions based on data. Our platform offers comprehensive comparisons, detailed analyses, and practical examples to help you navigate the complexities of statistical analysis.
9.5. Final Thoughts
In summary, understanding how the mean and median compare is essential for effective data analysis. By considering the data’s distribution, the presence of outliers, and the specific analytical goals, you can choose the most appropriate measure of central tendency and gain valuable insights.
10. Frequently Asked Questions (FAQs)
1. When should I use the mean instead of the median?
Use the mean when your data is
