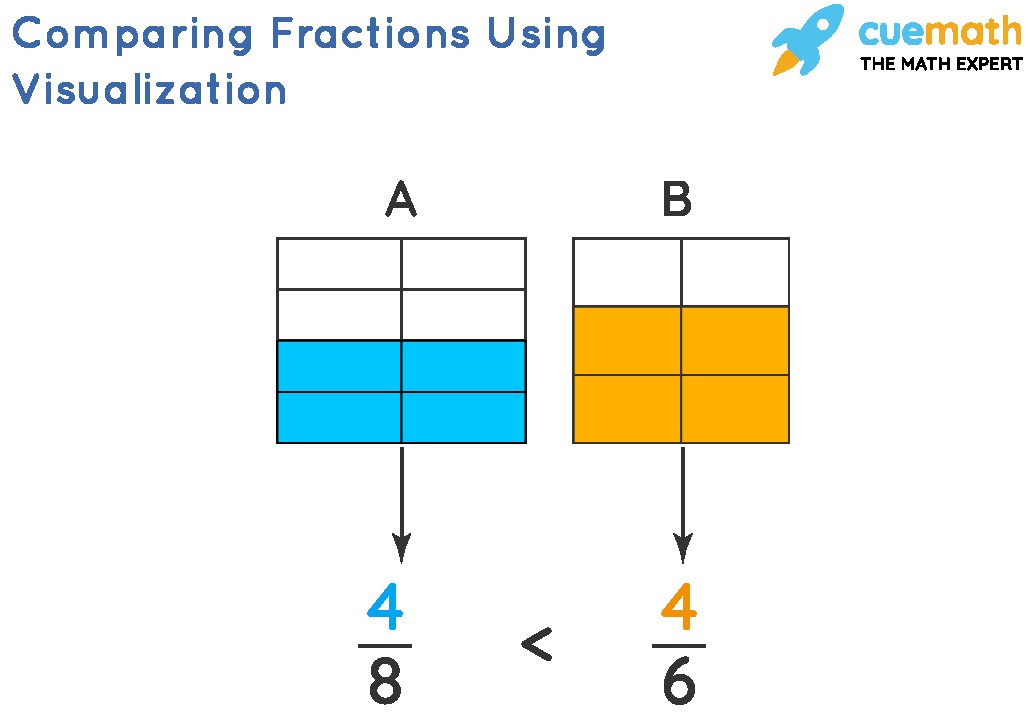
Comparing fractions is a fundamental math skill used daily, from adjusting recipes to calculating discounts. This guide provides clear, step-by-step instructions on various methods for comparing fractions, ensuring you confidently determine which fraction is larger or smaller.
Understanding Fractions
Before comparing fractions, let’s review the basics. A fraction represents a part of a whole. It consists of two numbers separated by a line:
- Numerator: The top number, indicating how many parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
Comparing Fractions with the Same Denominator
When fractions have the same denominator, comparing them is straightforward. The fraction with the larger numerator is the larger fraction.
Example:
Compare 3/5 and 2/5.
Both fractions have a denominator of 5. Since 3 is greater than 2, 3/5 is greater than 2/5 (3/5 > 2/5).
Comparing Fractions with Different Denominators
Comparing fractions with different denominators requires a few extra steps. Here are two common methods:
1. Finding the Least Common Denominator (LCD)
- Find the Least Common Multiple (LCM) of the two denominators. The LCM is the smallest number that both denominators divide into evenly.
- Convert each fraction to an equivalent fraction with the LCM as the denominator. Multiply both the numerator and denominator by the same number to achieve this.
- Compare the numerators of the new fractions. The fraction with the larger numerator is the larger fraction.
Example:
Compare 2/3 and 3/4.
- The LCM of 3 and 4 is 12.
- Convert 2/3 to an equivalent fraction with a denominator of 12: (2/3) * (4/4) = 8/12
- Convert 3/4 to an equivalent fraction with a denominator of 12: (3/4) * (3/3) = 9/12
- Since 9 is greater than 8, 3/4 is greater than 2/3 (3/4 > 2/3).
2. Cross-Multiplication
- Multiply the numerator of the first fraction by the denominator of the second fraction. Write the product next to the first fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction. Write the product next to the second fraction.
- Compare the products. The larger product indicates the larger fraction.
Example:
Compare 1/2 and 3/4.
- 1 * 4 = 4 (write 4 next to 1/2)
- 3 * 2 = 6 (write 6 next to 3/4)
- Since 6 is greater than 4, 3/4 is greater than 1/2 (3/4 > 1/2).
Decimal Method for Comparing Fractions
Another method involves converting fractions to decimals:
- Divide the numerator by the denominator for each fraction.
- Compare the resulting decimals. The larger decimal represents the larger fraction.
Example:
Compare 4/5 and 6/8.
- 4/5 = 0.8
- 6/8 = 0.75
- Since 0.8 is greater than 0.75, 4/5 is greater than 6/8 (4/5 > 6/8).
Conclusion
Comparing fractions is essential for various mathematical operations. By understanding these methods—comparing like denominators, finding the least common denominator, cross-multiplication, and converting to decimals—you can accurately compare fractions and confidently tackle any fraction-related problem. Practice these techniques to solidify your understanding and improve your math skills.