When comparing two populations, the larger the standard deviation typically indicates greater variability within that population; COMPARE.EDU.VN provides tools and resources to help you understand and compare statistical data effectively. This increased variability can significantly impact statistical analyses and the interpretation of results. Dive into data comparison, statistical variance, and population analysis.
1. Understanding Standard Deviation
Standard deviation is a fundamental concept in statistics that measures the dispersion of a dataset relative to its mean. It quantifies how much the individual data points deviate from the average value. A smaller standard deviation indicates that data points are clustered closely around the mean, suggesting less variability. Conversely, a larger standard deviation signifies that data points are more spread out, indicating greater variability.
1.1. Definition of Standard Deviation
Standard deviation, often denoted by the symbol σ (sigma) for a population or s for a sample, is the square root of the variance. The variance itself is the average of the squared differences from the mean.
Mathematically, the standard deviation for a population is calculated as:
[
sigma = sqrt{frac{sum_{i=1}^{N}(x_i – mu)^2}{N}}
]
Where:
- ( sigma ) is the population standard deviation
- ( x_i ) represents each value in the population
- ( mu ) is the population mean
- ( N ) is the number of values in the population
For a sample, the formula is:
[
s = sqrt{frac{sum_{i=1}^{n}(x_i – bar{x})^2}{n-1}}
]
Where:
- ( s ) is the sample standard deviation
- ( x_i ) represents each value in the sample
- ( bar{x} ) is the sample mean
- ( n ) is the number of values in the sample
The denominator ( n-1 ) in the sample standard deviation formula is known as Bessel’s correction. It provides an unbiased estimate of the population standard deviation.
1.2. Interpreting Standard Deviation
Interpreting standard deviation involves understanding its relationship to the spread of data. Here are some key points:
- Low Standard Deviation: A low standard deviation means that the data points tend to be close to the mean. This indicates consistency and less variability within the dataset. In practical terms, if you’re measuring the heights of students in a class and the standard deviation is low, it suggests that most students are around the same height.
- High Standard Deviation: A high standard deviation indicates that the data points are spread out over a wider range of values. This implies greater variability and less consistency. For example, if you’re analyzing the incomes of residents in a city and the standard deviation is high, it suggests a wide disparity in income levels.
- Zero Standard Deviation: A standard deviation of zero occurs when all data points are identical. In this case, there is no variability because every value is the same as the mean.
1.3. Standard Deviation vs. Variance
Standard deviation and variance are closely related, but they are not the same. Variance is the average of the squared differences from the mean, while standard deviation is the square root of the variance.
- Variance: Variance provides a measure of the average squared deviation from the mean. It is useful for mathematical calculations but is not on the same scale as the original data, making it harder to interpret directly.
- Standard Deviation: Standard deviation, being the square root of the variance, is expressed in the same units as the original data. This makes it easier to understand and compare with the mean and individual data points.
For example, if you’re measuring test scores and the variance is 100, the standard deviation would be ( sqrt{100} = 10 ). This means that, on average, test scores deviate by 10 points from the mean.
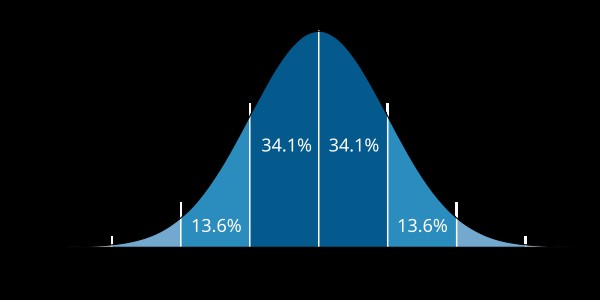
1.4. Empirical Rule (68-95-99.7 Rule)
The empirical rule, also known as the 68-95-99.7 rule, provides a guideline for understanding the spread of data in a normal distribution. It states that:
- Approximately 68% of the data falls within one standard deviation of the mean.
- Approximately 95% of the data falls within two standard deviations of the mean.
- Approximately 99.7% of the data falls within three standard deviations of the mean.
This rule is particularly useful for quickly assessing the distribution of data and identifying potential outliers. For instance, if the mean height of adults is 5’10” with a standard deviation of 3 inches, the empirical rule suggests that about 68% of adults are between 5’7″ and 6’1″, and about 95% are between 5’4″ and 6’4″.
 Interpreting Standard Deviation
Interpreting Standard Deviation
1.5. Applications in Real-World Scenarios
Standard deviation is used across various fields to analyze data and make informed decisions. Here are some examples:
- Finance: In finance, standard deviation is used to measure the volatility of an investment. A high standard deviation indicates that the investment’s returns are highly variable and potentially riskier.
- Healthcare: In healthcare, standard deviation can be used to analyze patient data, such as blood pressure or cholesterol levels. It helps in identifying patients with unusual or concerning variations.
- Manufacturing: In manufacturing, standard deviation is used to monitor the consistency of product quality. A low standard deviation indicates that the products are consistently meeting the required specifications.
- Education: In education, standard deviation can be used to analyze test scores and evaluate the performance of students. It helps in identifying areas where students may need additional support.
- Sports: In sports, standard deviation can be used to analyze player performance metrics, such as batting averages in baseball or scoring averages in basketball. It helps in assessing the consistency of a player’s performance.
Understanding standard deviation is essential for interpreting data and making informed decisions in various fields. Whether you’re analyzing financial investments, healthcare data, or manufacturing processes, standard deviation provides valuable insights into the variability and consistency of the data. For more detailed comparisons and analyses, visit COMPARE.EDU.VN.
2. Standard Deviation and Population Variability
When comparing two populations, the standard deviation plays a crucial role in understanding the variability within each group. A larger standard deviation indicates greater diversity or spread in the data, which can have significant implications for statistical analyses and decision-making.
2.1. High Standard Deviation Indicates Greater Variability
A high standard deviation signifies that the data points are widely dispersed from the mean. This implies that there is a greater degree of heterogeneity within the population. In practical terms, this means that the values in the population are more varied and less consistent.
For example, consider two groups of students taking a test. If Group A has a high standard deviation in their scores, it means that the scores are spread out over a wide range. Some students may have scored very high, while others scored very low. On the other hand, if Group B has a low standard deviation, it means that the scores are clustered closely around the mean, indicating more consistent performance among the students.
2.2. Impact on Statistical Analyses
The magnitude of the standard deviation can significantly impact statistical analyses, particularly when comparing means between two populations. Here are some key considerations:
- T-tests: When conducting t-tests to compare the means of two groups, the standard deviation is used to calculate the standard error, which affects the test statistic and p-value. A larger standard deviation leads to a larger standard error, making it more difficult to detect a significant difference between the means.
- Confidence Intervals: The width of a confidence interval is also influenced by the standard deviation. A larger standard deviation results in a wider confidence interval, reflecting greater uncertainty about the true population mean.
- Effect Size: Effect size measures, such as Cohen’s d, quantify the magnitude of the difference between two groups relative to the standard deviation. A larger standard deviation can reduce the effect size, making it harder to detect a practically significant difference.
2.3. Comparing Populations with Different Standard Deviations
When comparing two populations with different standard deviations, it is important to consider the implications for the statistical tests you use. Here are some common scenarios and appropriate approaches:
- Equal Variances: If the standard deviations of the two populations are approximately equal, you can use a pooled t-test, which assumes that the variances are the same. This test combines the data from both groups to estimate a common variance.
- Unequal Variances: If the standard deviations are significantly different, you should use an unequal variance t-test (also known as Welch’s t-test), which does not assume equal variances. This test adjusts the degrees of freedom to account for the difference in variances.
- Non-parametric Tests: If the data are not normally distributed or if the sample sizes are small, non-parametric tests such as the Mann-Whitney U test may be more appropriate. These tests do not rely on assumptions about the distribution of the data.
2.4. Examples in Various Fields
The impact of standard deviation on population variability can be illustrated with examples from different fields:
- Healthcare: When comparing the effectiveness of two drugs, a high standard deviation in patient outcomes for one drug may indicate that the drug’s effects are highly variable, possibly due to individual differences in metabolism or response to treatment.
- Finance: In finance, when comparing the performance of two investment portfolios, a high standard deviation in one portfolio’s returns indicates greater volatility and risk compared to a portfolio with a lower standard deviation.
- Marketing: In marketing, when comparing the effectiveness of two advertising campaigns, a high standard deviation in customer response to one campaign may indicate that the campaign is more effective for some segments of the population but less effective for others.
- Education: When comparing the performance of students in two different schools, a high standard deviation in test scores in one school may indicate a wider range of student abilities or differences in teaching quality.
2.5. Importance of Sample Size
The sample size also plays a critical role when comparing populations with different standard deviations. A larger sample size provides more statistical power, making it easier to detect a significant difference between the means, even when the standard deviations are large. Conversely, a small sample size may not provide enough power to detect a real difference, especially if the standard deviations are high.
In summary, when comparing two populations, the standard deviation provides valuable information about the variability within each group. A larger standard deviation indicates greater diversity and can impact statistical analyses and decision-making. Understanding these implications is crucial for drawing accurate conclusions and making informed choices. For more detailed comparisons and analyses, visit COMPARE.EDU.VN.
3. Statistical Tests and Standard Deviation
The standard deviation profoundly influences the choice and interpretation of statistical tests when comparing populations. Understanding how standard deviation affects these tests is crucial for drawing accurate conclusions.
3.1. T-Tests: Pooled vs. Unequal Variance
T-tests are commonly used to determine if there is a significant difference between the means of two groups. There are two main types of t-tests:
- Pooled Variance T-Test: This test assumes that the variances (and thus the standard deviations) of the two populations are equal. It pools the data from both groups to estimate a common variance.
- Unequal Variance T-Test (Welch’s T-Test): This test does not assume equal variances and is used when the standard deviations of the two populations are significantly different. It adjusts the degrees of freedom to account for the difference in variances.
The choice between these two tests depends on whether the assumption of equal variances is met. If the standard deviations are similar, the pooled variance t-test is more powerful. However, if the standard deviations are significantly different, the unequal variance t-test is more appropriate.
3.2. F-Test for Equality of Variances
Before conducting a t-test, it is common to perform an F-test to determine if the variances of the two populations are equal. The F-test compares the ratio of the variances:
[
F = frac{s_1^2}{s_2^2}
]
Where:
- ( s_1^2 ) is the variance of the first sample
- ( s_2^2 ) is the variance of the second sample
If the F-test is significant, it suggests that the variances are unequal, and the unequal variance t-test should be used.
3.3. Non-Parametric Tests: Mann-Whitney U Test
When the data are not normally distributed or when the sample sizes are small, non-parametric tests may be more appropriate. The Mann-Whitney U test is a non-parametric test that compares the medians of two groups. It does not assume that the data are normally distributed and is less sensitive to outliers.
The Mann-Whitney U test is particularly useful when the standard deviations of the two populations are very different or when the data violate the assumptions of parametric tests.
3.4. ANOVA: Analysis of Variance
ANOVA (Analysis of Variance) is used to compare the means of three or more groups. Like t-tests, ANOVA assumes that the variances of the populations are equal. If the variances are unequal, modifications to ANOVA, such as Welch’s ANOVA, can be used.
ANOVA partitions the total variance in the data into different sources of variation, allowing you to determine if there are significant differences between the group means.
3.5. Effect Size Measures: Cohen’s D
Effect size measures quantify the magnitude of the difference between two groups. Cohen’s d is a commonly used effect size measure that expresses the difference between two means in terms of standard deviation units:
[
d = frac{bar{x}_1 – bar{x}2}{s{pooled}}
]
Where:
- ( bar{x}_1 ) is the mean of the first group
- ( bar{x}_2 ) is the mean of the second group
- ( s_{pooled} ) is the pooled standard deviation
Cohen’s d provides a standardized measure of the difference between the means, making it easier to compare results across different studies.
3.6. Interpreting P-Values and Significance Levels
The p-value is the probability of observing a test statistic as extreme as, or more extreme than, the one calculated from the sample data, assuming that the null hypothesis is true. A small p-value (typically less than 0.05) indicates strong evidence against the null hypothesis, leading to its rejection.
The significance level (( alpha )) is the threshold for rejecting the null hypothesis. It represents the probability of making a Type I error (rejecting the null hypothesis when it is actually true). Common significance levels are 0.05 and 0.01.
When interpreting p-values, it is important to consider the sample size and the standard deviation. A large standard deviation can increase the p-value, making it more difficult to detect a significant difference.
In summary, the standard deviation plays a crucial role in the choice and interpretation of statistical tests. Understanding how standard deviation affects t-tests, F-tests, non-parametric tests, and effect size measures is essential for drawing accurate conclusions and making informed decisions. For more detailed comparisons and analyses, visit COMPARE.EDU.VN.
4. Practical Implications of Varying Standard Deviations
The standard deviation’s magnitude has several practical implications when comparing different populations or datasets. These implications affect how we interpret data and make decisions based on statistical analyses.
4.1. Impact on Decision-Making
Varying standard deviations can significantly impact decision-making processes across various fields. Here are some examples:
- Investment Decisions: In finance, a high standard deviation in an investment portfolio’s returns indicates greater volatility and risk. Investors may prefer investments with lower standard deviations to reduce the uncertainty of returns. Conversely, some investors may be willing to accept higher standard deviations for the potential of higher returns.
- Healthcare Decisions: When choosing between two medical treatments, a high standard deviation in patient outcomes for one treatment may indicate that the treatment’s effects are highly variable. Doctors and patients may prefer treatments with lower standard deviations to ensure more predictable results.
- Marketing Decisions: In marketing, a high standard deviation in customer response to an advertising campaign may indicate that the campaign is more effective for some segments of the population but less effective for others. Marketers may need to tailor their strategies to target specific groups.
- Educational Decisions: When evaluating the effectiveness of different teaching methods, a high standard deviation in student performance for one method may indicate that the method is more effective for some students but less effective for others. Educators may need to adopt a variety of teaching methods to accommodate different learning styles.
4.2. Risk Assessment
Standard deviation is a key factor in risk assessment. A higher standard deviation generally indicates a higher level of risk. This is because a larger standard deviation means that the data points are more spread out, making it more likely to encounter extreme values.
For example, in financial risk management, standard deviation is used to measure the volatility of assets and portfolios. A higher standard deviation indicates a greater potential for large gains or losses, increasing the risk of the investment.
4.3. Quality Control
In manufacturing and quality control, standard deviation is used to monitor the consistency of product quality. A low standard deviation indicates that the products are consistently meeting the required specifications. A high standard deviation may indicate that the manufacturing process is not well-controlled, leading to inconsistent product quality.
Statistical process control (SPC) charts, such as X-bar charts and R charts, are used to monitor the mean and range (which is related to the standard deviation) of a process over time. These charts help identify when a process is out of control and needs to be adjusted.
4.4. Performance Evaluation
Standard deviation is used in performance evaluation to assess the consistency of performance. For example, in sports, a player with a low standard deviation in their performance metrics (such as batting average or scoring average) is considered more consistent than a player with a high standard deviation.
In business, standard deviation can be used to evaluate the performance of employees or departments. A low standard deviation in performance metrics indicates more consistent performance, while a high standard deviation may indicate variability in performance that needs to be addressed.
4.5. Data Interpretation
When interpreting data, it is important to consider the standard deviation in addition to the mean. The mean provides information about the average value, while the standard deviation provides information about the variability around the mean.
For example, if you are comparing the salaries of employees in two companies, it is not enough to just compare the average salaries. You also need to consider the standard deviations. If one company has a higher average salary but also a higher standard deviation, it may indicate that there is a greater disparity in salaries within that company.
4.6. Sample Size Considerations
The sample size plays a crucial role when interpreting standard deviations. A larger sample size provides a more accurate estimate of the population standard deviation. With small sample sizes, the standard deviation may be more sensitive to outliers and may not accurately reflect the true variability in the population.
When comparing standard deviations between two groups, it is important to ensure that the sample sizes are large enough to provide reliable estimates. Statistical power analysis can be used to determine the appropriate sample size needed to detect a significant difference between the standard deviations.
In summary, varying standard deviations have several practical implications for decision-making, risk assessment, quality control, performance evaluation, and data interpretation. Understanding these implications is essential for making informed choices and drawing accurate conclusions. For more detailed comparisons and analyses, visit COMPARE.EDU.VN.
5. Common Misconceptions About Standard Deviation
Standard deviation is a fundamental statistical concept, but it is often misunderstood. Clearing up these misconceptions is essential for accurate data interpretation and analysis.
5.1. Standard Deviation Equals Error
One common misconception is that standard deviation represents error. While standard deviation does measure variability, it is not necessarily indicative of mistakes or errors in the data. Instead, it reflects the natural variation that exists within a population.
For example, if you measure the heights of students in a class, the standard deviation reflects the natural variation in heights among the students. It does not mean that there were errors in the measurement process.
5.2. Higher Standard Deviation Is Always Bad
Another misconception is that a higher standard deviation is always undesirable. While a high standard deviation can indicate greater variability and risk, it is not always a negative thing. In some cases, variability may be desirable or expected.
For example, in a stock portfolio, a higher standard deviation may indicate the potential for higher returns, although it also comes with higher risk. In other situations, variability may be a sign of innovation or creativity.
5.3. Standard Deviation Can Be Negative
Standard deviation is always a non-negative value. It is calculated as the square root of the variance, and the square root of a number cannot be negative. A standard deviation of zero indicates that there is no variability in the data, meaning all data points are identical.
5.4. Standard Deviation Is the Same as Standard Error
Standard deviation and standard error are related but distinct concepts. Standard deviation measures the variability within a sample or population, while standard error measures the variability of a sample statistic, such as the mean.
The standard error is calculated as the standard deviation divided by the square root of the sample size:
[
SE = frac{sigma}{sqrt{n}}
]
Where:
- ( SE ) is the standard error
- ( sigma ) is the standard deviation
- ( n ) is the sample size
Standard error is used to estimate the precision of a sample statistic and is used in hypothesis testing and confidence interval calculations.
5.5. Standard Deviation Applies Only to Normal Distributions
While standard deviation is often associated with normal distributions, it can be calculated for any dataset, regardless of its distribution. However, the interpretation of standard deviation may be different for non-normal distributions.
For example, the empirical rule (68-95-99.7 rule) applies only to normal distributions. For non-normal distributions, other rules or methods may be needed to interpret the spread of the data.
5.6. Standard Deviation Is Not Affected by Outliers
Standard deviation is sensitive to outliers, which are extreme values that are far from the mean. Outliers can significantly increase the standard deviation, leading to a misleading representation of the variability in the data.
When outliers are present, it may be appropriate to use robust measures of variability, such as the interquartile range (IQR), which is less sensitive to extreme values.
5.7. Standard Deviation Is Unaffected by Sample Size
While the standard deviation of a population is a fixed value, the standard deviation of a sample is affected by the sample size. As the sample size increases, the sample standard deviation becomes a more accurate estimate of the population standard deviation.
With small sample sizes, the sample standard deviation may be more variable and may not accurately reflect the true variability in the population.
5.8. Standard Deviation Can Be Used to Compare Different Variables
Standard deviation can only be used to compare the variability of the same variable across different groups or populations. It cannot be used to compare the variability of different variables, as they may be measured on different scales.
For example, you cannot compare the standard deviation of heights to the standard deviation of weights, as they are measured in different units.
Clearing up these common misconceptions about standard deviation is essential for accurate data interpretation and analysis. Understanding the true meaning of standard deviation allows for more informed decision-making and a better understanding of the variability in the data. For more detailed comparisons and analyses, visit COMPARE.EDU.VN.
6. Advanced Concepts Related to Standard Deviation
Beyond the basic understanding of standard deviation, several advanced concepts build upon this foundation. These concepts are crucial for more sophisticated statistical analyses and interpretations.
6.1. Coefficient of Variation (CV)
The coefficient of variation (CV) is a standardized measure of dispersion of a probability distribution or frequency distribution. It is defined as the ratio of the standard deviation to the mean:
[
CV = frac{sigma}{mu}
]
Where:
- ( CV ) is the coefficient of variation
- ( sigma ) is the standard deviation
- ( mu ) is the mean
The CV is useful for comparing the variability of datasets with different means or different units of measurement. It expresses the standard deviation as a percentage of the mean, making it easier to compare the relative variability.
For example, if you are comparing the variability of salaries in two different companies, the CV can provide a more meaningful comparison than the standard deviation alone, as it takes into account the different average salary levels.
6.2. Standard Deviation of a Portfolio
In finance, the standard deviation of a portfolio measures the total risk of the portfolio. It takes into account the standard deviations of the individual assets in the portfolio, as well as the correlations between the assets.
The formula for the standard deviation of a two-asset portfolio is:
[
sigma_p = sqrt{w_1^2sigma_1^2 + w_2^2sigma_2^2 + 2w_1w2rho{12}sigma_1sigma_2}
]
Where:
- ( sigma_p ) is the standard deviation of the portfolio
- ( w_1 ) and ( w_2 ) are the weights of assets 1 and 2 in the portfolio
- ( sigma_1 ) and ( sigma_2 ) are the standard deviations of assets 1 and 2
- ( rho_{12} ) is the correlation between assets 1 and 2
The standard deviation of a portfolio is influenced by the diversification effect, which reduces the overall risk of the portfolio by combining assets with low or negative correlations.
6.3. Standard Deviation in Regression Analysis
In regression analysis, standard deviation is used to measure the variability of the residuals, which are the differences between the observed values and the predicted values. The standard deviation of the residuals is known as the standard error of the estimate.
The standard error of the estimate provides a measure of the accuracy of the regression model. A lower standard error indicates that the model provides more accurate predictions.
6.4. Standard Deviation in Time Series Analysis
In time series analysis, standard deviation is used to measure the volatility of a time series. Volatility is a measure of the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns.
High volatility indicates that the time series is subject to large and frequent fluctuations, while low volatility indicates that the time series is more stable.
6.5. Standard Deviation in Machine Learning
In machine learning, standard deviation is used for feature scaling, which is the process of normalizing the range of independent variables or features of data. Feature scaling is important because features with different scales can affect the performance of machine learning algorithms.
One common feature scaling technique is standardization, which involves subtracting the mean and dividing by the standard deviation:
[
x_{scaled} = frac{x – mu}{sigma}
]
Where:
- ( x_{scaled} ) is the scaled value
- ( x ) is the original value
- ( mu ) is the mean
- ( sigma ) is the standard deviation
Standardization ensures that all features have a similar range of values, which can improve the convergence and performance of machine learning algorithms.
Understanding these advanced concepts related to standard deviation allows for more sophisticated statistical analyses and interpretations. These concepts are essential for professionals in fields such as finance, statistics, and machine learning. For more detailed comparisons and analyses, visit COMPARE.EDU.VN.
7. Tools and Resources for Calculating Standard Deviation
Calculating standard deviation can be done using various tools and resources, ranging from simple calculators to advanced statistical software. Choosing the right tool depends on the complexity of the data and the specific needs of the analysis.
7.1. Calculators
Basic calculators can be used to calculate standard deviation for small datasets. These calculators typically require you to input the data points and then perform the necessary calculations manually.
There are also online standard deviation calculators that can simplify the process. These calculators allow you to input the data points and then automatically calculate the mean, variance, and standard deviation.
7.2. Spreadsheet Software: Microsoft Excel, Google Sheets
Spreadsheet software such as Microsoft Excel and Google Sheets provides built-in functions for calculating standard deviation. These functions can be used to calculate standard deviation for larger datasets and can also be used to perform more complex statistical analyses.
In Excel, the STDEV.S function calculates the sample standard deviation, while the STDEV.P function calculates the population standard deviation. Google Sheets provides similar functions, STDEV and STDEVP, respectively.
7.3. Statistical Software Packages: SPSS, SAS, R
Statistical software packages such as SPSS, SAS, and R provide a wide range of tools for calculating standard deviation and performing more advanced statistical analyses. These packages are designed for handling large and complex datasets and provide a variety of statistical procedures and visualizations.
- SPSS (Statistical Package for the Social Sciences): SPSS is a user-friendly statistical software package that is widely used in the social sciences, healthcare, and market research. It provides a graphical user interface and a wide range of statistical procedures.
- SAS (Statistical Analysis System): SAS is a powerful statistical software package that is used in a variety of industries, including finance, healthcare, and manufacturing. It provides a command-line interface and a wide range of statistical procedures.
- R: R is a free and open-source statistical software package that is widely used in academia and research. It provides a command-line interface and a wide range of statistical procedures and visualizations.
7.4. Programming Languages: Python, MATLAB
Programming languages such as Python and MATLAB provide libraries for calculating standard deviation and performing more advanced statistical analyses. These languages are flexible and powerful and can be used to automate statistical analyses and create custom statistical procedures.
- Python: Python is a versatile programming language that provides libraries such as NumPy and SciPy for calculating standard deviation and performing statistical analyses. These libraries provide functions for calculating the mean, variance, and standard deviation, as well as more advanced statistical procedures.
- MATLAB (Matrix Laboratory): MATLAB is a programming language and numerical computing environment that is widely used in engineering, science, and mathematics. It provides a wide range of toolboxes for performing statistical analyses and creating visualizations.
7.5. Online Statistical Tools
There are also a variety of online statistical tools that can be used to calculate standard deviation and perform statistical analyses. These tools are typically web-based and can be accessed from any device with an internet connection.
Some popular online statistical tools include:
- GraphPad Prism: GraphPad Prism is a statistical software package that is designed for scientific research. It provides a user-friendly interface and a wide range of statistical procedures and visualizations.
- VassarStats: VassarStats is a website that provides a variety of online statistical tools and resources. It includes calculators for calculating standard deviation and performing hypothesis tests.
Choosing the right tool for calculating standard deviation depends on the complexity of the data and the specific needs of the analysis. Basic calculators and spreadsheet software are suitable for small datasets and simple analyses, while statistical software packages and programming languages are more appropriate for larger datasets and more advanced analyses. For more detailed comparisons and analyses, visit COMPARE.EDU.VN.
8. Case Studies Illustrating Standard Deviation
To further illustrate the practical implications of standard deviation, let’s examine several case studies across different fields.
8.1. Case Study 1: Comparing Investment Portfolio Risk
Scenario: An investor is comparing two investment portfolios, Portfolio A and Portfolio B, to determine which is less risky.
Data:
- Portfolio A: Average annual return of 10%, standard deviation of 15%
- Portfolio B: Average annual return of 12%, standard deviation of 20%
Analysis:
- Portfolio A has a lower standard deviation (15%) compared to Portfolio B (20%). This indicates that Portfolio A is less volatile and less risky than Portfolio B.
- Although Portfolio B has a higher average annual return (12%) compared to Portfolio A (10%), the higher standard deviation suggests that the returns are more variable and unpredictable.
Conclusion:
The investor may prefer Portfolio A if they are risk-averse, as it offers a lower standard deviation and more consistent returns. However, if the investor is willing to take on more risk for the potential of higher returns, they may choose Portfolio B.
8.2. Case Study 2: Evaluating Manufacturing Process Quality
Scenario: A manufacturing company is evaluating the quality of two production processes, Process X and Process Y, to determine which is more consistent.
Data:
- Process X: Average product dimension of 5.0 cm, standard deviation of 0.1 cm
- Process Y: Average product dimension of 5.0 cm, standard deviation of 0.2 cm
Analysis:
- Process X has a lower standard deviation (0.1 cm) compared to Process Y (0.2 cm). This indicates that Process X is more consistent and produces products with dimensions closer to the target value.
- Although both processes have the same average product dimension (5.0 cm), the higher standard deviation in Process Y suggests that the product dimensions are more variable and may deviate more from the target value.
Conclusion:
The manufacturing company may prefer Process X as it offers a lower standard deviation and more consistent product quality. This can lead to fewer defects and higher customer satisfaction.
8.3. Case Study 3: Assessing Student Performance in Two Schools
Scenario: An educational researcher is comparing the performance of students in two schools, School A and School B, to determine which school has more consistent student achievement.
Data:
- School A: Average test score of 75, standard deviation of 10
- School B: Average test score of 75, standard deviation of 15
Analysis:
- School A has a lower standard deviation (10) compared to School B (15). This indicates that student achievement in School A is more consistent and less variable.
- Although both schools have the same average test score (75), the higher standard deviation in School B suggests that there is a wider range of student abilities and achievement levels.
Conclusion:
The educational researcher may conclude that School A has more consistent student achievement and may be more effective in providing a uniform educational experience. However, School B may be more effective in catering to a diverse range of student abilities.
8.4. Case Study 4: Comparing the Effectiveness of Two Drugs
Scenario: A pharmaceutical company is comparing the effectiveness of two drugs, Drug A and Drug B, in treating a particular medical condition.
Data:
- Drug A: Average reduction in symptoms of 50%, standard deviation of 20%
- Drug B: Average reduction in symptoms of 50%, standard deviation of 10%
Analysis:
- Drug B has a lower standard deviation (10%) compared to Drug A (20%). This indicates that Drug B is more consistent and produces more predictable results.
- Although both drugs have the same average reduction in symptoms (50%), the higher standard deviation in Drug A suggests that the drug’s effects are more variable and may depend more on individual patient characteristics.
Conclusion:
The pharmaceutical company may prefer Drug B as it offers a lower standard deviation and more consistent results. This can lead to more predictable treatment outcomes and higher patient satisfaction.
8.5. Case Study 5: Analyzing Customer Satisfaction Scores
Scenario: A company is analyzing customer satisfaction scores for two different products, Product C and Product D, to determine which product has more consistent customer satisfaction.
Data:
- Product C: Average satisfaction score of 4.0, standard deviation of 0.5
- Product D: Average satisfaction score of 4.0, standard deviation of 1.0
Analysis:
- Product C has a lower standard deviation (0.5) compared to Product D (1.0). This indicates that customer satisfaction for Product C is more consistent and less variable.
- Although both products have the same average satisfaction score (4.0), the higher standard deviation in Product D suggests that there is a wider range of customer opinions and satisfaction levels.
Conclusion:
The company may prefer Product C as it offers a lower standard deviation and more consistent customer satisfaction. This can lead to more predictable customer loyalty and higher brand reputation.
These case studies illustrate how standard deviation can be used to compare the variability of different datasets and make informed decisions in various fields. Understanding the implications of standard deviation is essential for accurate data interpretation and analysis. For more detailed comparisons and analyses, visit compare.edu.vn.
9. FAQ About Standard Deviation
Here are some frequently asked questions about standard deviation, along with detailed answers to help clarify any confusion.
9.1. What is the difference between standard deviation and variance?
Standard deviation and variance are both measures of dispersion, but they are calculated differently and have different units.
- Variance: Variance is the average of the squared differences from the mean. It provides a measure of