What Is The Meaning Of Compare In Maths?

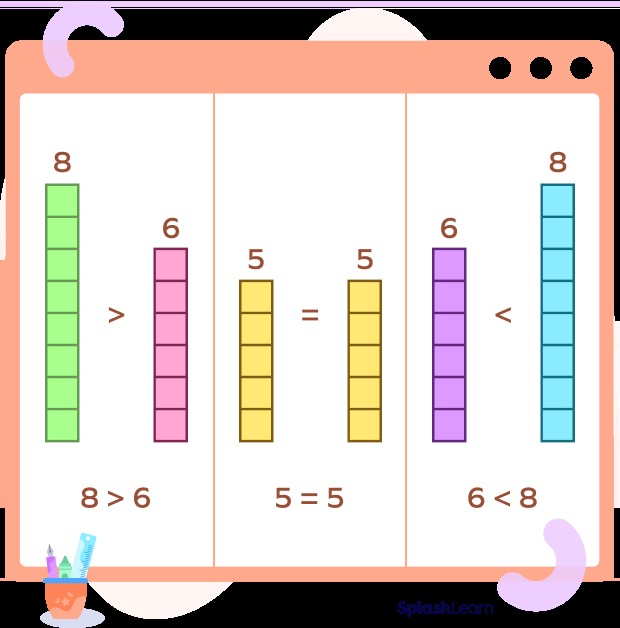
What Is The Meaning Of Compare In Maths? Comparing in mathematics involves assessing the relationship between two or more quantities to determine if they are equal, or if one is greater or less than the other, a skill essential for problem-solving and decision-making, and at COMPARE.EDU.VN, we help you master it. We provide comprehensive guides and examples to clarify these concepts. By understanding the nuances of mathematical comparison, you enhance your analytical skills, improving logical thinking and quantitative reasoning, ultimately enabling informed choices and effective problem-solving across diverse scenarios.

1. Understanding the Basics of Comparison in Math

The term “compare” in mathematics refers to the process of examining two or more quantities, values, or mathematical objects to determine their similarities, differences, and relative magnitudes. This comparison helps in understanding the relationship between the entities being examined, facilitating decision-making and problem-solving. Comparing numbers, sets, functions, or geometric shapes allows us to establish order, identify patterns, and make informed judgments based on their properties and characteristics.

1.1. Core Concepts of Mathematical Comparison

Mathematical comparison involves several core concepts that form the foundation for more complex analyses. These concepts include:

Equality: Determining whether two quantities are the same.
Inequality: Ascertaining whether one quantity is greater than or less than another.
Magnitude: Evaluating the size or extent of a quantity.
Ratio: Expressing the relative size of two quantities.
Proportion: Establishing the equivalence of two ratios.

1.2. Importance of Comparison in Mathematical Thinking

Comparison is integral to mathematical thinking as it promotes analytical reasoning and critical evaluation. By comparing different mathematical objects, students and professionals can identify patterns, make inferences, and develop a deeper understanding of mathematical principles. This skill is essential for:

Problem-Solving: Identifying relevant information and choosing appropriate strategies.
Decision-Making: Evaluating different options and selecting the best course of action.
Logical Reasoning: Constructing valid arguments and drawing logical conclusions.
Quantitative Analysis: Interpreting data and making predictions based on numerical trends.

2. Symbols and Notations Used in Comparison

In mathematics, specific symbols and notations are used to denote different types of comparisons. These symbols provide a concise and standardized way to express relationships between quantities.

2.1. Basic Comparison Symbols

The most commonly used comparison symbols include:

= (Equal to): Indicates that two quantities have the same value.
≠ (Not equal to): Indicates that two quantities do not have the same value.
> (Greater than): Indicates that the first quantity is larger than the second.
< (Less than): Indicates that the first quantity is smaller than the second.
≥ (Greater than or equal to): Indicates that the first quantity is either larger than or equal to the second.
≤ (Less than or equal to): Indicates that the first quantity is either smaller than or equal to the second.

2.2. Advanced Notations in Comparison

In more advanced mathematical contexts, additional notations are used to express complex comparisons:

≈ (Approximately equal to): Indicates that two quantities are nearly equal.
∝ (Proportional to): Indicates that two quantities vary in direct proportion.
≡ (Identical to): Indicates that two expressions are equivalent for all values of their variables.
∈ (Element of): Indicates that an element belongs to a set.
⊆ (Subset of): Indicates that one set is contained within another set.

These symbols and notations provide a precise language for expressing mathematical relationships, enabling clear communication and rigorous analysis.

3. Comparing Numbers: Whole Numbers, Integers, and Rational Numbers

Comparing numbers involves assessing their relative values and positions on the number line. This process differs slightly depending on the type of numbers being compared.

3.1. Comparing Whole Numbers

Whole numbers are non-negative integers (0, 1, 2, 3, …). Comparing whole numbers involves determining which number is larger or smaller.

Method: Counting the number of digits. A number with more digits is larger. If the numbers have the same number of digits, compare the digits from left to right until a difference is found.
Example: Comparing 345 and 298. Both have three digits. Comparing the hundreds place, 3 > 2, so 345 > 298.

3.2. Comparing Integers

Integers include all whole numbers and their negative counterparts (… -3, -2, -1, 0, 1, 2, 3…). Comparing integers requires considering their sign and magnitude.

Rules:
- Positive integers are always greater than negative integers.
- When comparing two positive integers, the larger number is greater.
- When comparing two negative integers, the number closer to zero is greater.
Example: Comparing -7 and -3. Since -3 is closer to zero, -3 > -7.

3.3. Comparing Rational Numbers

Rational numbers can be expressed as a fraction p/q, where p and q are integers and q ≠ 0. Comparing rational numbers involves converting them to a common denominator or decimal form.

Method 1: Common Denominator:
- Find the least common multiple (LCM) of the denominators.
- Convert each fraction to an equivalent fraction with the common denominator.
- Compare the numerators. The fraction with the larger numerator is greater.
Method 2: Decimal Conversion:
- Convert each fraction to its decimal equivalent.
- Compare the decimal values.
Example: Comparing 2/5 and 3/7.
- LCM of 5 and 7 is 35.
- 2/5 = 14/35 and 3/7 = 15/35.
- Since 15 > 14, 3/7 > 2/5.

4. Comparing Fractions: Like and Unlike Fractions

Fractions represent parts of a whole and can be compared to determine their relative sizes. The comparison method depends on whether the fractions have the same denominator (like fractions) or different denominators (unlike fractions).

4.1. Comparing Like Fractions

Like fractions have the same denominator. Comparing them is straightforward: simply compare the numerators.

Rule: The fraction with the larger numerator is greater.
Example: Comparing 3/8 and 5/8. Since 5 > 3, 5/8 > 3/8.

4.2. Comparing Unlike Fractions

Unlike fractions have different denominators. To compare them, you must first convert them to equivalent fractions with a common denominator.

Method 1: Finding a Common Denominator:
- Determine the least common multiple (LCM) of the denominators.
- Convert each fraction to an equivalent fraction with the LCM as the denominator.
- Compare the numerators.
Method 2: Cross Multiplication:
- Multiply the numerator of the first fraction by the denominator of the second fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the results.
Example: Comparing 2/3 and 3/4.
- LCM of 3 and 4 is 12.
- 2/3 = 8/12 and 3/4 = 9/12.
- Since 9 > 8, 3/4 > 2/3.
- Alternatively, using cross multiplication: 2 4 = 8 and 3 3 = 9. Since 9 > 8, 3/4 > 2/3.

5. Comparing Decimals: Place Value and Significant Digits

Decimals are numbers expressed in base 10, using a decimal point to separate the whole number part from the fractional part. Comparing decimals involves examining their place values and significant digits.

5.1. Understanding Place Value in Decimals

Each digit in a decimal number has a specific place value. From left to right after the decimal point, the place values are tenths, hundredths, thousandths, and so on.

Example: In the number 45.678, 6 is in the tenths place, 7 is in the hundredths place, and 8 is in the thousandths place.

5.2. Comparing Decimals Using Place Value

To compare decimals:

Step 1: Compare the whole number parts. If they are different, the decimal with the larger whole number part is greater.
Step 2: If the whole number parts are the same, compare the digits in the tenths place.
Step 3: Continue comparing digits in successive place values (hundredths, thousandths, etc.) until a difference is found.
Step 4: If one decimal has fewer digits than the other, you can add zeros to the end of the shorter decimal to make the number of digits equal.
Example: Comparing 3.45 and 3.425.
- The whole number parts are the same (3).
- The tenths place is the same (4).
- Comparing the hundredths place, 5 > 2, so 3.45 > 3.425.

5.3. Significant Digits and Their Role in Comparison

Significant digits are the digits in a number that carry meaningful information about its precision. In scientific and engineering contexts, the number of significant digits indicates the accuracy of a measurement.

Rules for Identifying Significant Digits:
- All non-zero digits are significant.
- Zeros between non-zero digits are significant.
- Leading zeros are not significant.
- Trailing zeros in a number with a decimal point are significant.
Example: In the number 0.00340, the significant digits are 3, 4, and 0. The leading zeros are not significant.

When comparing numbers with different numbers of significant digits, it’s essential to consider the level of precision each number represents.

6. Comparing Algebraic Expressions and Equations

Algebraic expressions and equations involve variables, constants, and mathematical operations. Comparing them requires evaluating their values and understanding their properties.

6.1. Comparing Algebraic Expressions

Algebraic expressions are combinations of variables, constants, and operations. To compare two or more expressions:

Step 1: Simplify each expression by combining like terms and applying the order of operations (PEMDAS/BODMAS).
Step 2: Evaluate the expressions by substituting specific values for the variables.
Step 3: Compare the resulting values.
Example: Comparing 3x + 5 and 2x + 8 for x = 2.
- 3x + 5 = 3(2) + 5 = 6 + 5 = 11
- 2x + 8 = 2(2) + 8 = 4 + 8 = 12
- Since 12 > 11, 2x + 8 > 3x + 5 when x = 2.

6.2. Comparing Algebraic Equations

Algebraic equations are statements that two expressions are equal. To compare equations:

Step 1: Solve each equation for the variable.
Step 2: Compare the solutions.
Example: Comparing 2x + 3 = 7 and 3x – 5 = 4.
- Solving 2x + 3 = 7 gives 2x = 4, so x = 2.
- Solving 3x – 5 = 4 gives 3x = 9, so x = 3.
- Since 3 > 2, the solution to 3x – 5 = 4 is greater than the solution to 2x + 3 = 7.

6.3. Inequalities and Their Comparison

Inequalities are mathematical statements that compare two expressions using inequality symbols (>, <, ≥, ≤). Comparing inequalities involves determining the range of values that satisfy each inequality.

Method:
- Solve each inequality for the variable.
- Represent the solutions on a number line.
- Compare the ranges of values.
Example: Comparing x + 2 > 5 and 2x – 1 < 7.
- Solving x + 2 > 5 gives x > 3.
- Solving 2x – 1 < 7 gives 2x < 8, so x < 4.
- The solution to x + 2 > 5 is all x greater than 3, while the solution to 2x – 1 < 7 is all x less than 4.

7. Comparing Geometric Shapes and Figures

Comparing geometric shapes and figures involves assessing their properties, such as size, area, volume, angles, and side lengths.

7.1. Comparing Two-Dimensional Shapes

Two-dimensional shapes, like triangles, squares, and circles, can be compared based on:

Area: The amount of surface the shape covers.
Perimeter: The distance around the shape.
Angles: The measures of the angles within the shape.
Side Lengths: The lengths of the sides of the shape.
Example: Comparing a square with side length 5 and a rectangle with length 6 and width 4.
- Area of the square = 5 * 5 = 25.
- Area of the rectangle = 6 * 4 = 24.
- The square has a larger area.

7.2. Comparing Three-Dimensional Figures

Three-dimensional figures, like cubes, spheres, and cylinders, can be compared based on:

Volume: The amount of space the figure occupies.
Surface Area: The total area of the figure’s surfaces.
Dimensions: The lengths, widths, and heights of the figure.
Example: Comparing a cube with side length 3 and a sphere with radius 2.
- Volume of the cube = 3 3 3 = 27.
- Volume of the sphere = (4/3) π 2^3 ≈ 33.51.
- The sphere has a larger volume.

7.3. Congruence and Similarity in Geometry

Congruence: Two shapes are congruent if they have the same size and shape. Congruent shapes have identical properties.
Similarity: Two shapes are similar if they have the same shape but different sizes. Similar shapes have proportional side lengths and equal angles.

Comparing shapes for congruence and similarity involves checking if their corresponding properties are equal or proportional.

8. Real-Life Applications of Comparison in Mathematics

Comparison is a fundamental skill with numerous applications in everyday life and various professional fields.

8.1. Personal Finance and Budgeting

Comparing Prices: Evaluating the cost of different products or services to make informed purchasing decisions.
Budgeting: Assessing income and expenses to manage finances effectively.
Investment Analysis: Comparing investment options to maximize returns and minimize risks.
Loan Comparison: Evaluating interest rates and terms of different loans to choose the most favorable option.

8.2. Data Analysis and Statistics

Comparing Data Sets: Identifying trends, patterns, and anomalies in data.
Statistical Analysis: Evaluating the significance of differences between groups.
Market Research: Comparing consumer preferences and market trends to inform business strategies.
Scientific Research: Comparing experimental results with theoretical predictions.

8.3. Engineering and Technology

Comparing Designs: Evaluating the performance and efficiency of different engineering designs.
System Analysis: Comparing the characteristics of different systems to optimize performance.
Algorithm Comparison: Evaluating the efficiency and effectiveness of different algorithms.
Performance Testing: Comparing the performance of different products or systems under various conditions.

8.4. Everyday Decision-Making

Time Management: Comparing the time required for different tasks to prioritize activities effectively.
Distance and Travel: Comparing distances and routes to plan trips efficiently.
Cooking and Baking: Comparing ingredient quantities and ratios to achieve desired results.
Home Improvement: Comparing the costs and benefits of different renovation options.

9. Common Mistakes and How to Avoid Them

When comparing mathematical objects, several common mistakes can lead to incorrect conclusions. Being aware of these pitfalls and adopting strategies to avoid them is crucial for accurate analysis.

9.1. Ignoring Place Value in Decimals

A common mistake is to disregard the importance of place value when comparing decimals.

Mistake: Assuming that 0.12 is less than 0.099 because 12 is less than 99.
Correction: Recognize that 0.12 is 0.1 + 0.02, while 0.099 is 0.09 + 0.009. Therefore, 0.12 > 0.099.

9.2. Failing to Find a Common Denominator for Fractions

When comparing fractions, it’s essential to convert them to a common denominator.

Mistake: Assuming that 1/3 is greater than 1/2 because 3 is greater than 2.
Correction: Convert the fractions to a common denominator: 1/3 = 2/6 and 1/2 = 3/6. Therefore, 1/2 > 1/3.

9.3. Misinterpreting Negative Numbers

Understanding the order of negative numbers is crucial.

Mistake: Assuming that -5 is greater than -2 because 5 is greater than 2.
Correction: Remember that negative numbers decrease as their absolute value increases. Therefore, -2 > -5.

9.4. Overlooking Units of Measurement

When comparing quantities with units, it’s essential to ensure they are in the same units.

Mistake: Assuming that 1 meter is greater than 90 centimeters because 1 is greater than 90.
Correction: Convert the measurements to the same unit: 1 meter = 100 centimeters. Therefore, 1 meter > 90 centimeters.

9.5. Ignoring Significant Digits

In scientific and engineering contexts, ignoring significant digits can lead to inaccurate comparisons.

Mistake: Assuming that 2.5 is equal to 2.500 without considering precision.
Correction: Recognize that 2.5 has two significant digits, while 2.500 has four. The latter is more precise.

10. Practice Problems and Solutions

To reinforce your understanding of comparison in mathematics, here are some practice problems with detailed solutions.

10.1. Problem 1: Comparing Fractions

Which fraction is greater: 3/5 or 5/8?

Solution:
- Find a common denominator: LCM of 5 and 8 is 40.
- Convert the fractions: 3/5 = 24/40 and 5/8 = 25/40.
- Compare the numerators: 25 > 24.
- Therefore, 5/8 > 3/5.

10.2. Problem 2: Comparing Decimals

Which decimal is smaller: 0.45 or 0.405?

Solution:
- Compare the tenths place: Both are 4.
- Compare the hundredths place: 5 > 0.
- Therefore, 0.405 < 0.45.

10.3. Problem 3: Comparing Integers

Which integer is greater: -12 or -5?

Solution:
- Remember that negative numbers decrease as their absolute value increases.
- Therefore, -5 > -12.

10.4. Problem 4: Comparing Algebraic Expressions

Which expression is greater when x = 3: 2x + 1 or 3x – 2?

Solution:
- Evaluate 2x + 1: 2(3) + 1 = 7.
- Evaluate 3x – 2: 3(3) – 2 = 7.
- Therefore, 2x + 1 = 3x – 2 when x = 3.

10.5. Problem 5: Comparing Geometric Areas

Which has a larger area: a square with side length 4 or a circle with radius 3?

Solution:
- Area of the square = 4 * 4 = 16.
- Area of the circle = π * 3^2 ≈ 28.27.
- Therefore, the circle has a larger area.

11. Tools and Resources for Mathematical Comparison

Several tools and resources can assist in mathematical comparison, making the process more efficient and accurate.

11.1. Calculators and Software

Scientific Calculators: Perform complex calculations and comparisons.
Graphing Calculators: Visualize functions and compare their properties.
Spreadsheet Software (e.g., Microsoft Excel, Google Sheets): Organize data, perform calculations, and create charts for comparison.
Mathematical Software (e.g., MATLAB, Mathematica): Perform advanced mathematical computations and simulations.

11.2. Online Comparison Tools

Online Calculators: Perform specific calculations, such as fraction comparison or decimal conversion.
Graphing Websites (e.g., Desmos, GeoGebra): Visualize and compare functions and geometric shapes.
Data Analysis Websites: Analyze and compare data sets.

11.3. Educational Websites and Apps

Khan Academy: Offers free lessons and practice exercises on various mathematical topics.
COMPARE.EDU.VN: Offers comprehensive guides and examples to clarify mathematical concepts.
Mathway: Provides step-by-step solutions to mathematical problems.

12. Future Trends in Mathematical Comparison

The field of mathematical comparison is continuously evolving with advancements in technology and computational methods.

12.1. Big Data and Data Analytics

The increasing availability of big data is driving the development of new techniques for data analysis and comparison. These techniques enable the identification of patterns, trends, and relationships in large datasets.

12.2. Machine Learning and Artificial Intelligence

Machine learning algorithms are being used to automate and optimize the process of mathematical comparison. AI-powered tools can analyze complex data, identify anomalies, and make predictions based on historical trends.

12.3. Visualization and Interactive Tools

Interactive visualization tools are enhancing the way mathematical objects are compared. These tools allow users to explore data, manipulate parameters, and visualize the effects of different comparisons in real-time.

12.4. Interdisciplinary Applications

Mathematical comparison is increasingly being applied in interdisciplinary fields, such as finance, economics, biology, and environmental science. These applications require the development of new mathematical models and techniques for comparing complex systems.

13. Conclusion: Mastering the Art of Mathematical Comparison

Comparing is a foundational skill in mathematics, essential for problem-solving, decision-making, and analytical thinking. This comprehensive guide has covered the core concepts, symbols, methods, and applications of comparison in various mathematical contexts. By understanding the nuances of mathematical comparison and utilizing the tools and resources available, you can enhance your analytical skills and make informed choices in diverse scenarios.

Remember, the key to mastering mathematical comparison is consistent practice and a willingness to explore new techniques and applications. Whether you are a student, professional, or simply a curious learner, the ability to compare mathematical objects effectively will empower you to tackle complex problems and make sound judgments.

For more in-depth resources and assistance, visit COMPARE.EDU.VN, where you can find comprehensive guides, examples, and interactive tools to further enhance your understanding of mathematical comparison.

Take the next step in your mathematical journey and unlock the power of comparison at COMPARE.EDU.VN today!

Contact Us:

Address: 333 Comparison Plaza, Choice City, CA 90210, United States

WhatsApp: +1 (626) 555-9090

Website: COMPARE.EDU.VN

14. FAQs About Comparing in Maths

1. What is the basic definition of compare in math?

Compare in math means to examine the similarities and differences between two or more numbers, quantities, or objects to determine their relative value, size, or characteristics.

2. What symbols are used to compare numbers?

The symbols used to compare numbers include:

= (equal to)
≠ (not equal to)
(greater than)
< (less than)
≥ (greater than or equal to)
≤ (less than or equal to)

3. How do you compare whole numbers?

To compare whole numbers, count the number of digits. A number with more digits is larger. If the numbers have the same number of digits, compare the digits from left to right until a difference is found.

4. How do you compare fractions with different denominators?

To compare fractions with different denominators, find the least common multiple (LCM) of the denominators. Convert each fraction to an equivalent fraction with the common denominator, then compare the numerators. The fraction with the larger numerator is greater.

5. How do you compare decimals?

To compare decimals, compare the whole number parts first. If they are the same, compare the digits in the tenths place, then the hundredths place, and so on, until a difference is found.

6. How does comparing in math apply to real life?

Comparing in math applies to real life in various ways, such as comparing prices while shopping, managing personal finances, analyzing data, making informed decisions, and problem-solving in engineering and technology.

7. What is congruence and similarity in geometry?

Congruence means two shapes have the same size and shape, while similarity means two shapes have the same shape but different sizes. Congruent shapes have identical properties, and similar shapes have proportional side lengths and equal angles.

8. What are some common mistakes when comparing mathematical objects?

Common mistakes include ignoring place value in decimals, failing to find a common denominator for fractions, misinterpreting negative numbers, overlooking units of measurement, and ignoring significant digits.

9. How does COMPARE.EDU.VN help with understanding mathematical comparison?

COMPARE.EDU.VN provides comprehensive guides, examples, and interactive tools to clarify mathematical concepts, enhance analytical skills, and make informed decisions in various scenarios.

10. What future trends are expected in mathematical comparison?

Future trends include the increasing use of big data, machine learning, artificial intelligence, visualization tools, and interdisciplinary applications in mathematical comparison.

Are you struggling to make informed decisions based on comparisons? Visit compare.edu.vn today and discover how our comprehensive resources can help you master the art of mathematical comparison. Make smarter choices with confidence!