Comparing fractions involves a systematic approach to determine which fraction holds a greater or lesser value, and COMPARE.EDU.VN offers a comprehensive guide to mastering this essential mathematical skill. This article will delve into various methods, including finding common denominators, using decimals, and cross-multiplication, to simplify the process of evaluating fractions and understanding their relative sizes and relative magnitude.
1. Understanding How To Compare Fractions
Comparing fractions is a fundamental mathematical skill that involves determining the relative size or value of two or more fractions. A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number), and the process of comparison is crucial in various real-life scenarios, from cooking to finance. When you compare fractions, you’re essentially figuring out which fraction represents a larger or smaller portion of the whole, or whether they represent the same portion, therefore are equal value.
1.1. What Exactly Is A Fraction?
At its core, a fraction is a way to represent a part of a whole. It consists of two main components: the numerator and the denominator. The numerator indicates how many parts of the whole we have, while the denominator indicates the total number of equal parts that make up the whole. For instance, in the fraction 3/4, the numerator (3) tells us that we have three parts, and the denominator (4) tells us that the whole is divided into four equal parts. Understanding this basic concept is essential before diving into comparing fractions.
1.2. Why Is Comparing Fractions Important?
The ability to compare fractions is not just a theoretical exercise; it has practical applications in numerous aspects of daily life. Whether you’re following a recipe, managing finances, or analyzing data, comparing fractions can help you make informed decisions. For example, if a recipe calls for 1/3 cup of sugar and another calls for 1/4 cup, comparing these fractions will tell you which recipe requires more sugar. Similarly, understanding how to compare fractions is essential in understanding ratios and proportions.
1.3. Key Terminologies To Know
Before we delve into the methods of comparing fractions, let’s familiarize ourselves with some key terminologies:
- Numerator: The top number in a fraction, indicating how many parts of the whole are being considered.
- Denominator: The bottom number in a fraction, indicating the total number of equal parts that make up the whole.
- Like Fractions: Fractions that have the same denominator.
- Unlike Fractions: Fractions that have different denominators.
- Equivalent Fractions: Fractions that represent the same value, even though they may have different numerators and denominators (e.g., 1/2 and 2/4).
2. Comparing Fractions With Same Denominators: A Straightforward Approach
When comparing fractions that share the same denominator, the process becomes remarkably simple. The guiding principle here is that the fraction with the larger numerator represents the greater value. This is because, when the denominators are the same, the fractions are divided into the same number of equal parts, so the fraction with more of those parts is larger.
2.1. The Basic Rule: Focus On The Numerator
The rule for comparing fractions with the same denominators is straightforward: the fraction with the larger numerator is the larger fraction. This is because both fractions represent parts of a whole that has been divided into the same number of pieces (as indicated by the common denominator). The fraction with the greater number of these pieces is therefore the larger fraction.
2.2. Illustrative Examples To Enhance Understanding
To solidify this concept, let’s consider a few examples:
- Example 1: Compare 3/7 and 5/7. Both fractions have the same denominator (7), so we compare the numerators. Since 5 > 3, we can conclude that 5/7 > 3/7.
- Example 2: Compare 1/4 and 3/4. Again, the denominators are the same (4), so we compare the numerators. Since 3 > 1, we know that 3/4 > 1/4.
- Example 3: Compare 2/9, 5/9 and 8/9. All fractions have the same denominator (9). Comparing the numerators: 2 < 5 < 8. Therefore, 2/9 < 5/9 < 8/9.
2.3. What If The Numerators And Denominators Are Equal?
In the special case where both the numerators and the denominators of two fractions are equal, the fractions are considered equal. For instance, 4/4 is equal to 1 whole, and any other fraction with the same numerator and denominator (e.g., 5/5, 6/6) will also be equal to 1 whole.
3. Overcoming The Challenge: Comparing Fractions With Different Denominators
Comparing fractions with different denominators requires a bit more work than comparing fractions with the same denominators. The key is to find a common denominator, which allows you to compare the fractions on an equal footing.
3.1. The Need For A Common Denominator
When fractions have different denominators, it’s like comparing apples and oranges. The fractions are divided into different numbers of parts, so it’s difficult to tell which one is larger without first converting them to a common denominator. Finding a common denominator allows you to express both fractions in terms of the same number of parts, making it easy to compare the numerators.
3.2. Finding The Least Common Multiple (LCM)
The most efficient way to find a common denominator is to determine the Least Common Multiple (LCM) of the original denominators. The LCM is the smallest number that is a multiple of both denominators. Once you’ve found the LCM, you can convert each fraction to an equivalent fraction with the LCM as the new denominator.
3.3. Steps To Convert Fractions To Like Denominators
Here’s a step-by-step guide to converting fractions to like denominators:
- Step 1: Identify the denominators of the fractions you want to compare.
- Step 2: Find the Least Common Multiple (LCM) of the denominators. This will be your common denominator.
- Step 3: For each fraction, determine what number you need to multiply the original denominator by to get the common denominator.
- Step 4: Multiply both the numerator and the denominator of each fraction by the number you found in step 3. This will give you an equivalent fraction with the common denominator.
- Step 5: Once all fractions have the same denominator, you can compare the numerators to determine which fraction is larger.
3.4. Real-World Examples
Let’s work through a couple of examples to illustrate this process:
-
Example 1: Compare 1/3 and 2/5.
- The denominators are 3 and 5.
- The LCM of 3 and 5 is 15.
- To convert 1/3 to a fraction with a denominator of 15, we multiply both the numerator and denominator by 5: (1 x 5) / (3 x 5) = 5/15.
- To convert 2/5 to a fraction with a denominator of 15, we multiply both the numerator and denominator by 3: (2 x 3) / (5 x 3) = 6/15.
- Now we can compare 5/15 and 6/15. Since 6 > 5, we know that 6/15 > 5/15, which means 2/5 > 1/3.
-
Example 2: Compare 3/4 and 5/8.
- The denominators are 4 and 8.
- The LCM of 4 and 8 is 8.
- To convert 3/4 to a fraction with a denominator of 8, we multiply both the numerator and denominator by 2: (3 x 2) / (4 x 2) = 6/8.
- 5/8 already has the desired denominator, so we don’t need to change it.
- Now we can compare 6/8 and 5/8. Since 6 > 5, we know that 6/8 > 5/8, which means 3/4 > 5/8.
-
Example 3: Compare 2/3, 3/5, and 1/2.
- The denominators are 3, 5, and 2.
- The LCM of 3, 5, and 2 is 30.
- Convert each fraction to have a denominator of 30:
- 2/3 = (2 x 10) / (3 x 10) = 20/30
- 3/5 = (3 x 6) / (5 x 6) = 18/30
- 1/2 = (1 x 15) / (2 x 15) = 15/30
- Now we can compare: 20/30 > 18/30 > 15/30, which means 2/3 > 3/5 > 1/2.
3.5. Special Case: Same Numerators, Different Denominators
There’s a shortcut for comparing fractions with the same numerators but different denominators: the fraction with the smaller denominator is the larger fraction. This is because, if you have the same number of parts (numerator), the parts are larger when the whole is divided into fewer pieces (smaller denominator). For example, 2/3 > 2/5 because thirds are larger than fifths.
4. Decimal Method: Converting Fractions To Decimals
Another effective method for comparing fractions is to convert them into decimal numbers. This approach is particularly useful when dealing with fractions that have large or complex denominators, as it simplifies the comparison process by expressing each fraction as a familiar decimal value.
4.1. The Process Of Decimal Conversion
To convert a fraction to a decimal, you simply divide the numerator by the denominator. The result is a decimal number that represents the same value as the original fraction. For instance, to convert 3/4 to a decimal, you would divide 3 by 4, which equals 0.75.
4.2. Comparing Decimal Values For Simplicity
Once you’ve converted all the fractions to decimals, comparing them becomes straightforward. You can simply compare the decimal values to determine which fraction is larger or smaller. For example, if you’ve converted 2/5 to 0.4 and 3/4 to 0.75, you can easily see that 0.75 > 0.4, which means 3/4 > 2/5.
4.3. Benefits And Scenarios For Using Decimals
The decimal method offers several benefits:
- Simplicity: Converting fractions to decimals simplifies the comparison process, especially when dealing with unlike denominators.
- Familiarity: Most people are more familiar with decimal numbers than fractions, making it easier to grasp the relative size of the values.
- Calculator-Friendly: This method is easily implemented using a calculator, which can be helpful when dealing with complex fractions.
However, it’s important to note that some fractions result in repeating decimals (e.g., 1/3 = 0.333…), which may require rounding and can introduce slight inaccuracies.
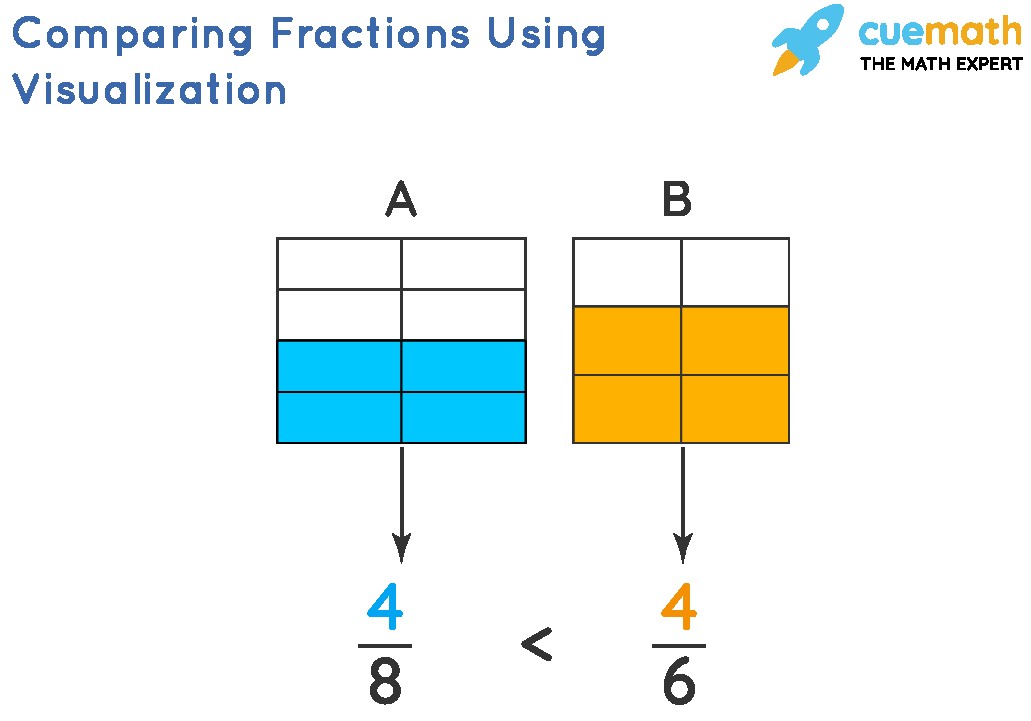
5. Visualizing Fractions: Using Models For Comparison
For many learners, visualizing fractions can make the comparison process more intuitive and understandable. Visual models provide a concrete representation of fractions, allowing you to see the relative sizes and easily determine which one is larger.
5.1. Employing Graphical Methods And Models
There are several types of visual models that can be used to compare fractions, including:
- Area Models: These models use shapes, such as circles or rectangles, to represent the whole, with the fraction representing the portion of the shape that is shaded or colored.
- Length Models: These models use lines or bars to represent the whole, with the fraction representing the length of a segment of the line or bar.
- Set Models: These models use a collection of objects to represent the whole, with the fraction representing the number of objects that are a certain color or type.
5.2. Making It Clear: How Visuals Aid Understanding
Visual models can be particularly helpful for comparing fractions with different denominators. By representing each fraction with a visual model, you can easily see which fraction covers a larger portion of the whole, even if the models are divided into different numbers of parts.
5.3. Example Case With Model A And Model B
For example, imagine you want to compare 1/3 and 1/4 using area models. You could draw two identical rectangles, divide one into three equal parts and shade one part to represent 1/3, and divide the other into four equal parts and shade one part to represent 1/4. By visually comparing the shaded areas, you can easily see that 1/3 covers a larger portion of the rectangle than 1/4, which means 1/3 > 1/4.
6. Cross Multiplication: A Quick Trick For Fraction Comparison
Cross multiplication is a quick and efficient method for comparing two fractions, especially when you don’t need to find a common denominator or convert to decimals. This technique involves multiplying the numerator of one fraction by the denominator of the other, and comparing the resulting products.
6.1. How To Apply Cross Multiplication
To compare two fractions using cross multiplication, follow these steps:
- Step 1: Write the two fractions you want to compare side by side. For example, let’s say you want to compare a/b and c/d.
- Step 2: Multiply the numerator of the first fraction (a) by the denominator of the second fraction (d). This gives you the product ad.
- Step 3: Multiply the numerator of the second fraction (c) by the denominator of the first fraction (b). This gives you the product bc.
- Step 4: Compare the two products, ad and bc. If ad > bc, then a/b > c/d. If ad < bc, then a/b < c/d. If ad = bc, then a/b = c/d.
6.2. Unveiling The Logic Behind Cross Multiplication
The logic behind cross multiplication lies in the fact that it’s essentially a shortcut for finding a common denominator. When you cross multiply, you’re multiplying both fractions by the denominators of the other, which is equivalent to finding a common denominator and comparing the numerators.
6.3. Using Cross Multiplication In Practice
Let’s illustrate this with a couple of examples:
-
Example 1: Compare 3/4 and 5/7.
- Cross multiply: (3 x 7) = 21 and (5 x 4) = 20.
- Since 21 > 20, we know that 3/4 > 5/7.
-
Example 2: Compare 2/5 and 4/10.
- Cross multiply: (2 x 10) = 20 and (4 x 5) = 20.
- Since 20 = 20, we know that 2/5 = 4/10.
7. Examples On Comparing Fractions
Let’s explore some examples of comparing fractions using the methods we’ve discussed.
7.1. Example 1
Why is 5/11 > 4/11? Can you explain?
Solution:
Comparing fractions becomes easier if the denominators are the same. 5/11 and 4/11 have the same denominators; hence, we can simply compare the fractions by observing the numerators. The fraction with a larger numerator will be the larger fraction. 5 > 4. Therefore, 5/11 > 4/11.
7.2. Example 2
Ryan was asked to prove that the given fractions: 4/6 and 6/9 are equal. Can you prove this using the LCM method?
Solution:
We can make the denominators the same by finding the LCM of the denominators of the given fractions. The LCM of 6 and 9 is 18. So, we will multiply 4/6 with 3/3, (4/6) × (3/3) = 12/18, and 6/9 with 2/2, (6/9) × (2/2) = 12/18, which will convert them to like fractions with the same denominators. The new fractions with the same denominators will be 12/18 and 12/18. Hence, both the fractions are equal: 4/6 = 6/9. Therefore, 4/6 = 6/9.
7.3. Example 3
Compare the fractions 5/8 and 7/12.
Solution: For comparing fractions with different denominators, we need to find the LCM of the denominators. The LCM of 8 and 12 is 24. So, let us multiply 5/8 with 3/3, that is, 5/8 × 3/3 = 15/24. Now, let us multiply 7/12 with 2/2, that is, 14/24. Now that we have like fractions 15/24 and 14/24, we can easily compare them. Since 15 > 14, 5/8 > 7/12. Therefore, 5/8 > 7/12.
8. Practice Questions On Comparing Fractions
Practice makes perfect. Try your hand at these practice questions to solidify your understanding of comparing fractions.
8.1. Question 1
Compare 2/7 and 4/9 using cross multiplication. Which fraction is larger?
8.2. Question 2
Arrange the following fractions in ascending order: 1/2, 2/5, 3/8.
9. Frequently Asked Questions (FAQs) On Comparing Fractions
Here are some frequently asked questions about comparing fractions, along with their answers.
9.1. What Does Comparing Fractions Mean?
Comparing fractions means comparing the given fractions in order to tell if one fraction is less than, greater than, or equal to the other fraction. Like whole numbers, we can compare fractions using the same symbols: <, >, and =. There are various methods and rules to compare fractions, depending upon the numerator and the denominator and the kind of fractions given.
9.2. What Is The Rule Of Comparing Fractions With The Same Denominator?
When the denominators of the given set of fractions are the same, the fraction with the smaller numerator is the smaller fraction and the fraction with the larger numerator is the larger fraction. When the numerators are equal, the fractions are considered to be equal. For example, if we need to compare 2/5 and 4/5, we just need to check and compare the numerators. Since 2 < 4, 2/5 < 4/5.
9.3. What Is The Rule When Comparing Fractions With The Same Numerator?
When the fractions have the same numerator, the fraction with the smaller denominator is greater. For example, let us compare fractions with the same numerator. The given fractions are 1/2, and 1/6. Now out of these, the fraction with the smaller denominator is 1/2. Thus, 1/2 is the larger of the given fractions.
9.4. What Are Equivalent Fractions?
The fractions that have different numerators and denominators but are equal in their values are called equivalent fractions. For example, 5/10, and 6/12 are equivalent fractions since both of them are equal to 1/2 when simplified.
9.5. What Is The Easiest Way Of Comparing Fractions?
The easiest and fastest way to compare fractions is to convert them into decimal numbers. The fraction with the larger decimal value is the larger fraction.
9.6. Why Do We Need To Compare Fractions?
Comparing fractions is an important component, which helps students develop their number sense about the fraction size. This helps them realize that the strategies they use to compare whole numbers do not necessarily apply while comparing fractions. For example, 1/4 is greater than 1/8 even though the whole number 8 is greater than 4.
9.7. How To Compare Fractions With Different Denominators?
In order to compare fractions with different denominators, we need to find the Least Common Multiple (LCM) of the denominators and convert the given fractions to like fractions by making their denominators the same and then the numerators can be easily compared. For example, let us compare 7/12 and 9/16.
- Step 1: Since the given fractions have different denominators, we will find the LCM of the denominators. The LCM of 12 and 16 = 48.
- Step 2: Now, we will convert the fractions in such a way that the denominators become the same. Let us multiply the first fraction with 4/4, that is, 7/12 × 4/4 = 28/48.
- Step 3: Now, let us multiply the second fraction with 3/3 that is, 9/16 × 3/3 = 27/48.
- Step 4: Compare the fractions: 28/48 and 27/48. Since the denominators are the same, we will compare the numerators, and we can see that 28 > 27.
- Step 5: The fraction with the larger numerator is the larger fraction, that is, 28/48 > 27/48. Therefore, 7/12 > 9/16
Conclusion: Make Informed Decisions With COMPARE.EDU.VN
Comparing fractions is a fundamental skill with applications in various aspects of life, and mastering it can empower you to make informed decisions in a variety of contexts. Whether you prefer finding common denominators, using decimals, visualizing models, or applying cross multiplication, understanding these methods will enhance your ability to compare fractions with confidence and accuracy.
Are you looking for a comprehensive platform to simplify your comparison tasks and make informed decisions? Visit COMPARE.EDU.VN today. At COMPARE.EDU.VN, we understand the challenges individuals face when comparing different options, whether it’s products, services, or ideas. That’s why we’ve created a user-friendly platform that provides detailed and objective comparisons to help you make the right choice. Our website offers a wide range of comparison articles across various categories, including education, technology, finance, and more. Our team of experts works diligently to gather accurate data, analyze information, and present it in an easy-to-understand format. We pride ourselves on delivering unbiased comparisons that highlight the pros and cons of each option, empowering you to make confident decisions.
Contact us:
- Address: 333 Comparison Plaza, Choice City, CA 90210, United States
- WhatsApp: +1 (626) 555-9090
- Website: compare.edu.vn
Start exploring our comparison articles now and unlock a world of informed decision-making.