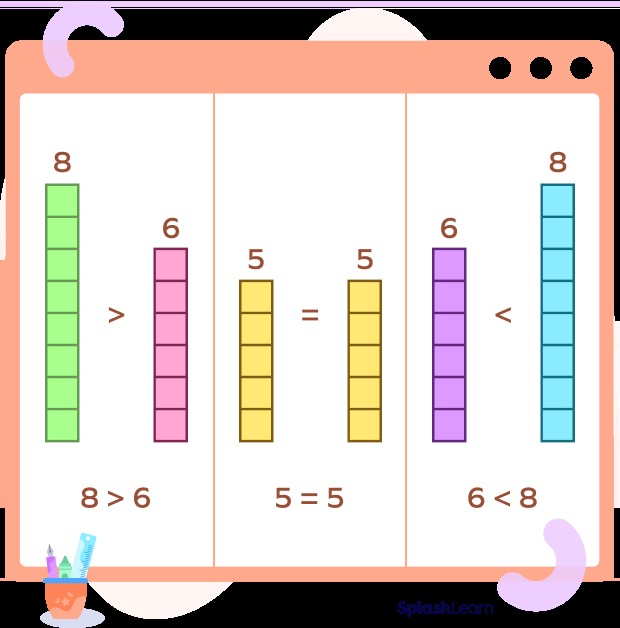
What Does It Mean To Compare Numbers? Discover how mathematical comparisons unveil relationships, order, and significance. At COMPARE.EDU.VN, we simplify these concepts, guiding you through numerical analysis for informed decisions. Explore number comparison techniques and their importance.
1. Understanding the Essence of Number Comparison
Comparing numbers is the cornerstone of mathematical understanding and decision-making. It involves assessing the relative value of two or more numbers to determine whether one is greater than, less than, or equal to the other. This fundamental process enables us to establish order, identify differences, and make informed judgments in various contexts.
1.1 Defining Number Comparison
Number comparison involves determining the relationship between two or more numerical values. It’s a process of evaluating magnitudes to establish a hierarchy or to identify similarities and differences. This process is crucial in mathematics, statistics, and everyday decision-making.
1.2 The Symbols of Comparison
In mathematical notation, specific symbols represent the relationships between numbers:
- Greater Than (>): Indicates that one number is larger than another.
- Less Than (<): Indicates that one number is smaller than another.
- Equal To (=): Indicates that two numbers have the same value.
- Greater Than or Equal To (≥): Indicates that one number is larger than or the same as another.
- Less Than or Equal To (≤): Indicates that one number is smaller than or the same as another.
2. Why is Comparing Numbers Important?
Comparing numbers is essential for numerous reasons, spanning from academic pursuits to practical applications in daily life. The ability to compare numbers effectively enables individuals to make informed decisions, solve problems, and understand the world around them.
2.1 Facilitating Decision-Making
Number comparison is fundamental to decision-making in various contexts. Whether it’s evaluating financial investments, comparing product prices, or assessing performance metrics, the ability to compare numbers helps individuals make rational choices.
2.2 Problem Solving
Many mathematical problems require comparing numbers to find solutions. Whether it’s determining the larger of two quantities, identifying the minimum value in a set, or establishing inequalities, number comparison is an indispensable tool for problem-solving.
2.3 Understanding Magnitude and Scale
Comparing numbers helps us understand the magnitude and scale of different quantities. By comparing values, we can grasp the relative size of objects, distances, or amounts, providing valuable insights into the world around us.
2.4 Mathematical Reasoning
Number comparison is integral to mathematical reasoning and logical thinking. It enables us to make inferences, draw conclusions, and develop arguments based on numerical evidence. This skill is crucial for success in mathematics and related fields.
3. Techniques for Comparing Numbers
Several techniques can be used to compare numbers, depending on the type of numbers and the level of precision required. These techniques range from simple visual comparisons to more sophisticated mathematical methods.
3.1 Visual Comparison
Visual comparison involves directly observing the relative sizes or quantities of numbers to determine their relationship. This technique is often used for comparing small numbers or quantities that can be easily visualized.
3.2 Number Line Comparison
A number line is a visual representation of numbers arranged in order along a line. Comparing numbers on a number line involves identifying their positions relative to each other. Numbers to the right are greater, while numbers to the left are smaller.
3.3 Place Value Comparison
Place value comparison is used for comparing whole numbers by examining the digits in each place value (ones, tens, hundreds, etc.). Start by comparing the digits in the highest place value. If they are equal, move to the next lower place value until a difference is found.
3.4 Fraction Comparison
Comparing fractions involves determining which fraction represents a larger or smaller portion of a whole. This can be done by finding a common denominator or by cross-multiplying.
3.5 Decimal Comparison
Comparing decimals involves examining the digits after the decimal point to determine which decimal represents a larger or smaller value. Start by comparing the digits in the tenths place, then the hundredths place, and so on, until a difference is found.
3.6 Percentage Comparison
Comparing percentages involves determining which percentage represents a larger or smaller proportion of a whole. This can be done by converting percentages to decimals or fractions and then comparing them.
4. Comparing Different Types of Numbers
Numbers come in various forms, including whole numbers, integers, fractions, decimals, and more. Each type of number requires a specific approach to comparison.
4.1 Comparing Whole Numbers
Whole numbers are non-negative integers (0, 1, 2, 3, …). To compare whole numbers, you can use place value comparison, number line comparison, or visual comparison.
4.2 Comparing Integers
Integers include both positive and negative whole numbers (…, -3, -2, -1, 0, 1, 2, 3, …). When comparing integers, remember that positive integers are always greater than negative integers. For negative integers, the number with the smaller absolute value is greater.
4.3 Comparing Fractions
Fractions represent parts of a whole. To compare fractions, you can find a common denominator and compare the numerators, or you can cross-multiply.
4.4 Comparing Decimals
Decimals are numbers that use a decimal point to represent fractions. To compare decimals, you can line up the decimal points and compare the digits in each place value.
4.5 Comparing Rational Numbers
Rational numbers can be expressed as fractions (a/b, where b ≠ 0). To compare rational numbers, you can convert them to a common denominator or use cross-multiplication.
4.6 Comparing Irrational Numbers
Irrational numbers cannot be expressed as fractions (e.g., √2, π). To compare irrational numbers, you can approximate them as decimals and then compare the decimal values.
5. Real-World Applications of Number Comparison
Number comparison is not just a theoretical concept; it has practical applications in various aspects of daily life and professional fields.
5.1 Financial Analysis
In finance, number comparison is used to evaluate investment opportunities, assess risk, and make informed financial decisions. Comparing returns, interest rates, and expenses helps individuals and organizations optimize their financial performance.
5.2 Business Decision Making
Businesses rely on number comparison to analyze market trends, evaluate sales performance, and make strategic decisions. Comparing revenue, costs, and profits helps companies identify opportunities for growth and improvement.
5.3 Scientific Research
Scientists use number comparison to analyze experimental data, test hypotheses, and draw conclusions. Comparing measurements, observations, and statistical values helps researchers validate their findings and advance scientific knowledge.
5.4 Engineering and Construction
Engineers and construction professionals use number comparison to design structures, calculate loads, and ensure safety. Comparing dimensions, material strengths, and stress values helps engineers create reliable and efficient designs.
5.5 Everyday Life
In everyday life, number comparison is used for various tasks, such as comparing prices while shopping, calculating distances while traveling, and managing time effectively. These skills help individuals make informed decisions and manage their resources efficiently.
6. Common Mistakes to Avoid When Comparing Numbers
While number comparison is a fundamental skill, it’s easy to make mistakes if you’re not careful. Here are some common mistakes to avoid:
6.1 Ignoring Place Value
Failing to consider the place value of digits can lead to incorrect comparisons, especially with decimals and large numbers.
6.2 Confusing Negative Numbers
Forgetting that negative numbers are smaller than positive numbers, and that the larger the absolute value of a negative number, the smaller it is.
6.3 Misinterpreting Fractions
Not finding a common denominator or cross-multiplying correctly can lead to errors when comparing fractions.
6.4 Overlooking Units
Forgetting to convert numbers to the same units before comparing them (e.g., comparing meters and centimeters without converting).
6.5 Not Considering Context
Failing to consider the context of the comparison, such as whether a higher or lower value is better in a particular situation.
7. Tips for Improving Number Comparison Skills
Improving your number comparison skills requires practice and attention to detail. Here are some tips to help you become more proficient:
7.1 Practice Regularly
Consistent practice is key to mastering number comparison. Work through exercises and problems that involve comparing different types of numbers.
7.2 Use Visual Aids
Number lines, charts, and diagrams can help you visualize numbers and their relationships, making comparisons easier.
7.3 Understand Place Value
Develop a strong understanding of place value to accurately compare whole numbers and decimals.
7.4 Review Fraction and Decimal Concepts
Ensure you have a solid grasp of fraction and decimal concepts to avoid errors when comparing these types of numbers.
7.5 Pay Attention to Units
Always pay attention to units and convert numbers to the same units before comparing them.
7.6 Check Your Work
Take the time to check your work and ensure you haven’t made any careless mistakes.
8. Delving Deeper: Advanced Number Comparison Concepts
Beyond the basics, there are more advanced concepts related to number comparison that are important in higher-level mathematics and various applications.
8.1 Comparing Complex Numbers
Complex numbers have both a real and an imaginary part. Comparing complex numbers involves comparing their magnitudes (absolute values) or their real and imaginary parts separately.
8.2 Comparing Matrices
Matrices are arrays of numbers. Comparing matrices can involve comparing their dimensions, individual elements, or properties such as determinants or eigenvalues.
8.3 Comparing Functions
Functions are mathematical relationships between sets of numbers. Comparing functions can involve comparing their values, derivatives, integrals, or other properties.
8.4 Comparing Sets
Sets are collections of distinct objects. Comparing sets can involve determining whether one set is a subset of another, whether they have any elements in common, or whether they are equal.
9. The Role of Technology in Number Comparison
Technology plays a significant role in number comparison, providing tools and resources that make it easier and more efficient.
9.1 Calculators
Calculators can quickly compare numbers, perform calculations, and display results with precision.
9.2 Spreadsheets
Spreadsheets like Microsoft Excel and Google Sheets provide powerful tools for organizing, analyzing, and comparing numerical data.
9.3 Statistical Software
Statistical software packages like SPSS and R provide advanced tools for comparing data sets, performing statistical tests, and generating visualizations.
9.4 Online Comparison Tools
Numerous online tools and websites allow you to compare numbers, prices, products, and services quickly and easily.
10. Number Comparison and Computational Thinking
Number comparison is closely related to computational thinking, a problem-solving approach that involves breaking down complex problems into smaller, more manageable parts.
10.1 Decomposition
Breaking down a complex number comparison problem into smaller, simpler comparisons.
10.2 Pattern Recognition
Identifying patterns and similarities in numerical data to make comparisons more efficient.
10.3 Abstraction
Focusing on the essential details of a number comparison problem and ignoring irrelevant information.
10.4 Algorithm Design
Developing step-by-step procedures (algorithms) for comparing numbers in a systematic way.
11. Examples of Number Comparison in Daily Life
Number comparison is a skill we use every day, often without even realizing it. Here are some examples of how number comparison is applied in daily life:
11.1 Shopping
Comparing prices of products to find the best deal.
11.2 Cooking
Comparing ingredient amounts in recipes to ensure accurate proportions.
11.3 Traveling
Comparing distances, times, and costs to plan the most efficient route.
11.4 Personal Finance
Comparing interest rates, loan terms, and investment returns to make informed financial decisions.
11.5 Health and Fitness
Comparing calorie counts, exercise durations, and weight measurements to track progress and maintain a healthy lifestyle.
12. Case Studies: Real-World Scenarios Involving Number Comparison
To further illustrate the importance and versatility of number comparison, let’s examine some real-world case studies.
12.1 Investment Analysis
An investor uses number comparison to evaluate different investment options, considering factors such as potential returns, risk levels, and historical performance. By comparing these numerical values, the investor can make an informed decision about where to allocate their capital.
12.2 Marketing Campaign Evaluation
A marketing team uses number comparison to assess the effectiveness of different advertising campaigns. By comparing metrics such as click-through rates, conversion rates, and return on investment, the team can determine which campaigns are most successful and allocate resources accordingly.
12.3 Manufacturing Process Optimization
A manufacturing company uses number comparison to optimize its production processes. By comparing metrics such as production time, defect rates, and material costs, the company can identify areas for improvement and implement changes to increase efficiency and reduce waste.
12.4 Healthcare Treatment Decisions
A healthcare provider uses number comparison to make treatment decisions for patients. By comparing factors such as the patient’s medical history, test results, and potential treatment outcomes, the provider can determine the most appropriate course of action.
13. Exercises to Sharpen Your Number Comparison Skills
To reinforce your understanding of number comparison and hone your skills, try the following exercises:
13.1 Compare the following pairs of numbers:
- 345 and 543
- -12 and -5
- 2/3 and 3/4
- 0.75 and 0.8
- √9 and 3.14
13.2 Arrange the following numbers in ascending order:
- 5, -2, 0, 8, -10
13.3 Solve the following word problems:
- A store sells a shirt for $25 and a pair of pants for $40. Which item is more expensive?
- A car travels 150 miles in 3 hours. Another car travels 200 miles in 4 hours. Which car is faster?
- A recipe calls for 1/2 cup of flour and 1/4 cup of sugar. Which ingredient is needed in greater quantity?
14. The Future of Number Comparison
As technology continues to advance, the future of number comparison is likely to involve even more sophisticated tools and techniques.
14.1 Artificial Intelligence
AI algorithms can automate number comparison tasks, analyze large datasets, and identify patterns and insights that humans might miss.
14.2 Machine Learning
Machine learning models can learn from data and improve their ability to compare numbers and make predictions over time.
14.3 Big Data Analytics
Big data analytics tools can process massive amounts of numerical data and provide real-time comparisons and insights.
14.4 Quantum Computing
Quantum computers have the potential to perform complex number comparisons and calculations much faster than classical computers.
15. Number Comparison: Ethical Considerations
While number comparison is a valuable tool, it’s important to use it ethically and responsibly.
15.1 Data Privacy
Protecting the privacy of individuals when comparing numerical data, especially in sensitive areas such as healthcare and finance.
15.2 Transparency
Being transparent about the methods and criteria used to compare numbers, to avoid misleading or biased results.
15.3 Fairness
Ensuring that number comparisons are fair and equitable, and do not discriminate against any particular group or individual.
15.4 Accountability
Taking responsibility for the accuracy and reliability of number comparisons, and correcting any errors or inaccuracies that may occur.
16. Connecting Number Comparison to Other Mathematical Concepts
Number comparison is not an isolated concept; it is closely connected to other areas of mathematics.
16.1 Algebra
Number comparison is used to solve inequalities, graph functions, and analyze equations.
16.2 Geometry
Number comparison is used to measure lengths, areas, and volumes, and to compare shapes and sizes.
16.3 Calculus
Number comparison is used to find limits, derivatives, and integrals, and to analyze the behavior of functions.
16.4 Statistics
Number comparison is used to calculate means, medians, and standard deviations, and to compare data sets and distributions.
17. Resources for Further Learning
To continue your journey of learning about number comparison, here are some valuable resources:
17.1 Textbooks
- “Basic Mathematics” by Serge Lang
- “Mathematics for the General Reader” by Colin Butler and Claire Knox
- “The Number System” by H. A. Thurston
17.2 Online Courses
- Khan Academy (Mathematics)
- Coursera (Mathematics for Machine Learning)
- edX (Introduction to Statistics)
17.3 Websites
- COMPARE.EDU.VN
- MathWorld (Wolfram Research)
- PlanetMath
17.4 Journals
- The American Mathematical Monthly
- The College Mathematics Journal
- Mathematics Magazine
18. FAQs About Number Comparison
18.1 What is the difference between comparing and ordering numbers?
Comparing numbers involves determining the relationship between two or more numbers, while ordering numbers involves arranging them in a sequence from smallest to largest or vice versa.
18.2 How do you compare fractions with different denominators?
To compare fractions with different denominators, you need to find a common denominator or use cross-multiplication.
18.3 What is the best way to compare decimals?
To compare decimals, line up the decimal points and compare the digits in each place value.
18.4 How do you compare negative numbers?
When comparing negative numbers, remember that the number with the smaller absolute value is greater.
18.5 What are some real-world applications of number comparison?
Real-world applications of number comparison include shopping, cooking, traveling, personal finance, and health and fitness.
19. Conclusion: Empowering Decisions Through Numerical Insight
Mastering the art of comparing numbers is not merely an academic exercise; it’s a fundamental skill that empowers individuals to make informed decisions, solve problems effectively, and navigate the complexities of the modern world. Whether you’re evaluating financial investments, analyzing scientific data, or simply comparing prices at the grocery store, the ability to compare numbers with confidence and accuracy is essential for success in all areas of life.
At COMPARE.EDU.VN, we are committed to providing you with the knowledge, tools, and resources you need to excel in number comparison and unlock your full potential. Explore our website to discover in-depth guides, practical exercises, and real-world case studies that will help you sharpen your skills and gain a competitive edge. Join our community of learners today and embark on a journey of numerical empowerment.
Ready to make smarter, more informed decisions? Visit COMPARE.EDU.VN now and discover the power of number comparison. Your journey to numerical mastery starts here. Contact us at 333 Comparison Plaza, Choice City, CA 90210, United States or Whatsapp: +1 (626) 555-9090. Visit our comparison website compare.edu.vn today.