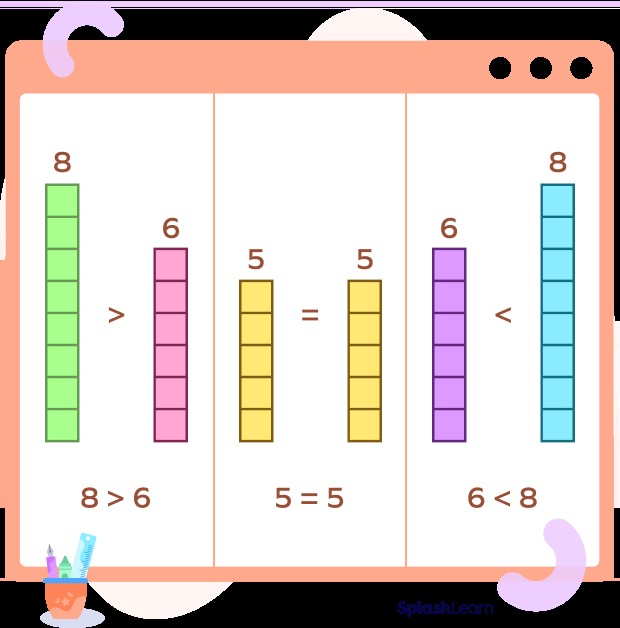
What Does Compare Mean In Math Terms? Find Out Here!

What Does Compare Mean In Math Terms? In mathematics, comparing involves determining whether one number is greater than, less than, or equal to another. Visit COMPARE.EDU.VN for detailed comparisons and informed decision-making using comparative analysis and relative magnitude assessments.

1. Understanding Comparison in Math

What does compare mean in math terms? Comparing, in a mathematical context, is the process of examining two or more quantities, values, or mathematical objects to determine their relative magnitude or characteristics. This process helps us understand the relationships between these entities, such as whether one is greater than, less than, or equal to another. Comparing numbers, sets, functions, or geometric shapes allows for a deeper analysis and informed decision-making. For example, comparing the prices of two products helps consumers decide which is more cost-effective, or comparing the sizes of two angles in geometry helps determine the shape of a figure.

1.1. Key Concepts in Mathematical Comparison

Understanding what does compare mean in math terms requires grasping several key concepts. These include:

• Inequalities: Mathematical statements that show the relationship between two values that are not equal. The symbols used are > (greater than), < (less than), ≥ (greater than or equal to), and ≤ (less than or equal to).
• Equality: A mathematical statement that asserts that two expressions have the same value. The symbol used is = (equal to).
• Magnitude: The size or extent of a quantity.
• Reference Point: A standard or base value used for comparison.
• Comparative Analysis: The process of evaluating different options or entities by comparing their characteristics.

1.2. Importance of Comparison in Mathematics

Comparison is fundamental to mathematical reasoning and problem-solving. It enables us to:

• Make Informed Decisions: By comparing values, we can determine the best course of action.
• Analyze Data: Comparison helps in identifying trends, patterns, and anomalies in datasets.
• Solve Equations and Inequalities: By comparing expressions, we can find solutions that satisfy given conditions.
• Understand Relationships: Comparison reveals how different mathematical entities relate to each other.
• Optimize Processes: By comparing different approaches, we can find the most efficient methods.

2. Methods of Comparing Numbers

What does compare mean in math terms encompasses various methods, each suited to different types of numbers and situations.

2.1. Comparing Whole Numbers

Whole numbers are non-negative integers (0, 1, 2, 3, …). Comparing whole numbers involves assessing their magnitude to determine which is larger or smaller.

Steps to Compare Whole Numbers:

1. Count the Digits: The number with more digits is generally larger. For example, 1,234 is greater than 987.
2. Compare Place Values: If the number of digits is the same, compare the digits from left to right, starting with the highest place value. The number with the larger digit in the highest place value is greater. For example, to compare 5,678 and 5,599, start by comparing the thousands place (both are 5). Then, compare the hundreds place: 6 is greater than 5, so 5,678 > 5,599.
3. Continue Comparing: If the digits in the highest place value are the same, continue comparing the digits in the next lower place value until you find a difference.

2.2. Comparing Integers

Integers include all whole numbers and their negative counterparts (… -3, -2, -1, 0, 1, 2, 3…). Comparing integers requires understanding the number line, where numbers increase from left to right.

Rules for Comparing Integers:

• Positive vs. Negative: Any positive integer is greater than any negative integer. For example, 3 > -5.
• Comparing Positives: Compare positive integers as you would whole numbers.
• Comparing Negatives: The negative integer with the smaller absolute value is greater. For example, -2 > -7 because -2 is closer to zero on the number line.

2.3. Comparing Fractions

Fractions represent parts of a whole. Comparing fractions can be more complex than comparing integers or whole numbers, especially when the fractions have different denominators.

Methods for Comparing Fractions:

1. Common Denominator: Find the least common denominator (LCD) of the fractions. Convert each fraction to an equivalent fraction with the LCD. Then, compare the numerators. The fraction with the larger numerator is greater.
   • Example: Compare (frac{3}{4}) and (frac{5}{6}). The LCD of 4 and 6 is 12. Convert the fractions:
     • (frac{3}{4} = frac{3 times 3}{4 times 3} = frac{9}{12})
     • (frac{5}{6} = frac{5 times 2}{6 times 2} = frac{10}{12})
       Since (frac{10}{12}) > (frac{9}{12}), then (frac{5}{6}) > (frac{3}{4}).
2. Cross-Multiplication: Multiply the numerator of the first fraction by the denominator of the second fraction, and multiply the numerator of the second fraction by the denominator of the first fraction. Compare the results.
   • Example: Compare (frac{2}{5}) and (frac{3}{7}).
     • (2 times 7 = 14)
     • (3 times 5 = 15)
       Since 15 > 14, then (frac{3}{7}) > (frac{2}{5}).
3. Decimal Conversion: Convert each fraction to a decimal and compare the decimals.
   • Example: Compare (frac{1}{4}) and (frac{2}{5}).
     • (frac{1}{4} = 0.25)
     • (frac{2}{5} = 0.4)
       Since 0.4 > 0.25, then (frac{2}{5}) > (frac{1}{4}).

2.4. Comparing Decimals

Decimals are numbers that contain a decimal point, representing fractions or parts of a whole.

Steps for Comparing Decimals:

1. Align Decimal Points: Write the numbers vertically, aligning the decimal points.
2. Compare Whole Number Parts: Compare the digits to the left of the decimal point. The number with the larger whole number part is greater.
3. Compare Decimal Parts: If the whole number parts are the same, compare the digits to the right of the decimal point, starting with the tenths place. If the digits in the tenths place are the same, move to the hundredths place, and so on, until you find a difference.
   • Example: Compare 4.567 and 4.589.
     • Both numbers have the same whole number part (4) and the same digit in the tenths place (5).
     • Compare the hundredths place: 8 > 6, so 4.589 > 4.567.

2.5. Comparing Rational Numbers

Rational numbers are numbers that can be expressed as a fraction (frac{p}{q}), where (p) and (q) are integers and (q neq 0). Comparing rational numbers is similar to comparing fractions.

Methods for Comparing Rational Numbers:

• Convert to Common Denominator: As with fractions, find the LCD and convert each rational number to an equivalent fraction with the LCD. Then, compare the numerators.
• Cross-Multiplication: Use cross-multiplication to compare the rational numbers.
• Convert to Decimals: Convert each rational number to a decimal and compare the decimals.

2.6. Comparing Irrational Numbers

Irrational numbers cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal representations (e.g., (sqrt{2}), (pi)).

Methods for Comparing Irrational Numbers:

• Approximate Decimal Values: Approximate the decimal values of the irrational numbers to a certain number of decimal places and compare the approximations.
  • Example: Compare (sqrt{2}) and (sqrt{3}).
    • (sqrt{2} approx 1.414)
    • (sqrt{3} approx 1.732)
      Since 1.732 > 1.414, then (sqrt{3}) > (sqrt{2}).
• Square the Numbers: If both numbers are positive, you can square them and compare the squares. This is useful for comparing square roots.
  • Example: Compare (sqrt{5}) and 2.
    • ((sqrt{5})^2 = 5)
    • (2^2 = 4)
      Since 5 > 4, then (sqrt{5}) > 2.

3. Mathematical Symbols Used in Comparisons

What does compare mean in math terms also involves knowing the symbols used to represent comparison:

• (= ) (Equal To): Indicates that two values are the same. For example, (5 = 5).
• (> ) (Greater Than): Indicates that the value on the left is larger than the value on the right. For example, (7 > 3).
• (< ) (Less Than): Indicates that the value on the left is smaller than the value on the right. For example, (2 < 6).
• (geq ) (Greater Than or Equal To): Indicates that the value on the left is either larger than or equal to the value on the right. For example, (x geq 4) means (x) can be 4 or any number greater than 4.
• (leq ) (Less Than or Equal To): Indicates that the value on the left is either smaller than or equal to the value on the right. For example, (y leq 10) means (y) can be 10 or any number less than 10.
• (neq ) (Not Equal To): Indicates that two values are not the same. For example, (8 neq 9).

4. Applications of Comparison in Mathematics

Understanding what does compare mean in math terms becomes clearer when we explore its applications.

4.1. Solving Inequalities

Inequalities are mathematical statements that compare two expressions using the symbols >, <, ≥, or ≤. Solving inequalities involves finding the range of values that satisfy the inequality.

Example:

Solve the inequality (3x + 5 < 14).

1. Subtract 5 from both sides: (3x < 9)
2. Divide both sides by 3: (x < 3)

This means any value of (x) that is less than 3 will satisfy the inequality.

4.2. Optimization Problems

Optimization problems involve finding the maximum or minimum value of a function subject to certain constraints. Comparison is used to determine which value is optimal.

Example:

A company wants to maximize its profit. They have two production options:

• Option A: Produces 100 units with a profit of $10 per unit.
• Option B: Produces 80 units with a profit of $12 per unit.

Compare the total profit for each option:

• Option A: (100 times $10 = $1000)
• Option B: (80 times $12 = $960)

Since $1000 > $960, Option A is more profitable.

4.3. Statistical Analysis

In statistics, comparison is used to analyze and interpret data. For example, comparing means, medians, and standard deviations of different datasets can reveal significant differences and trends.

Example:

Compare the test scores of two classes:

• Class A: Mean = 75, Standard Deviation = 10
• Class B: Mean = 80, Standard Deviation = 8

By comparing the means, we can see that Class B performed better on average. The standard deviations indicate the spread of the data, with Class B having less variability in scores.

4.4. Geometric Comparisons

In geometry, comparison is used to analyze shapes, sizes, and positions of geometric figures.

Examples:

• Comparing Angles: Determining if an angle is acute, right, or obtuse by comparing it to 90 degrees.
• Comparing Lengths: Measuring and comparing the lengths of line segments to determine congruence.
• Comparing Areas: Calculating and comparing the areas of different shapes to determine which is larger.

5. Real-Life Applications of Mathematical Comparison

What does compare mean in math terms extends far beyond the classroom, playing a crucial role in everyday decision-making.

5.1. Financial Decisions

• Comparing Prices: When shopping, comparing the prices of different brands or stores to find the best deal.
• Comparing Interest Rates: Evaluating different loan or investment options by comparing their interest rates.
• Budgeting: Comparing income and expenses to ensure financial stability.

5.2. Health and Fitness

• Comparing Nutritional Information: Reading food labels and comparing the nutritional content of different products.
• Tracking Progress: Comparing current weight or fitness levels to previous measurements to monitor progress.
• Comparing Workout Plans: Evaluating the effectiveness of different workout routines by comparing results.

5.3. Travel Planning

• Comparing Flight Prices: Using travel websites to compare the prices of flights from different airlines.
• Comparing Accommodation Options: Evaluating different hotels or rental properties by comparing prices, amenities, and reviews.
• Calculating Distances: Comparing distances between destinations to plan routes and estimate travel times.

5.4. Purchasing Decisions

• Comparing Product Features: Evaluating different products by comparing their features, specifications, and reviews.
• Comparing Warranties: Assessing the terms and conditions of warranties to determine the best coverage.
• Comparing Energy Efficiency: Evaluating the energy efficiency of appliances to reduce energy consumption and save money.

6. Advanced Concepts in Comparison

What does compare mean in math terms can also involve more complex mathematical concepts.

6.1. Calculus: Rates of Change

In calculus, comparing rates of change is essential. The derivative of a function gives the instantaneous rate of change, and comparing derivatives helps in understanding how different functions behave.

Example:

Compare the rates of growth of two populations:

• Population A: (P_A(t) = 100e^{0.05t})
• Population B: (P_B(t) = 50e^{0.08t})

Find the derivatives:

• (P_A'(t) = 5e^{0.05t})
• (P_B'(t) = 4e^{0.08t})

By comparing the derivatives, we can determine which population is growing faster at any given time (t).

6.2. Linear Algebra: Vector Comparison

In linear algebra, vectors can be compared based on their magnitude and direction. Dot products and cross products are used to determine the relationships between vectors.

Example:

Compare two vectors:

• (vec{u} = (3, 4))
• (vec{v} = (5, -2))

Calculate the dot product:

(vec{u} cdot vec{v} = (3 times 5) + (4 times -2) = 15 – 8 = 7)

The dot product can tell us about the angle between the vectors.

6.3. Set Theory: Set Comparison

In set theory, sets can be compared to determine relationships such as equality, subset, and superset.

Definitions:

• Equality: Two sets (A) and (B) are equal if they contain the same elements.
• Subset: Set (A) is a subset of set (B) if every element of (A) is also an element of (B).
• Superset: Set (A) is a superset of set (B) if every element of (B) is also an element of (A).

Example:

Compare the sets:

• (A = {1, 2, 3})
• (B = {3, 2, 1})
• (C = {1, 2, 3, 4})

(A) and (B) are equal because they contain the same elements in a different order. (A) is a subset of (C) because every element of (A) is also in (C). (C) is a superset of (A) for the same reason.

7. Tips for Accurate Mathematical Comparisons

To accurately what does compare mean in math terms, consider the following tips:

• Understand the Context: Know the type of numbers or mathematical objects you are comparing.
• Use Appropriate Methods: Choose the correct method for the type of comparison you are making (e.g., common denominator for fractions, aligning decimal points for decimals).
• Check for Common Units: Ensure that you are comparing values in the same units.
• Be Precise: Use accurate measurements and calculations.
• Consider the Scale: Understand the scale of the numbers you are comparing. A small difference might be significant for small numbers but negligible for large numbers.
• Double-Check Your Work: Review your comparisons to ensure accuracy.

8. Common Mistakes to Avoid

• Comparing Unlike Units: Ensure all values are in the same units before comparing.
• Ignoring Negative Signs: Remember that negative numbers have a different order than positive numbers.
• Incorrectly Converting Fractions: Make sure you convert fractions to a common denominator correctly.
• Rounding Errors: Avoid rounding numbers too early in the comparison process, as this can lead to inaccuracies.
• Misinterpreting Symbols: Understand the meaning of each comparison symbol ((=, >, <, geq, leq)).

9. Resources for Further Learning

To deepen your understanding of what does compare mean in math terms, consider these resources:

• Textbooks: Look for textbooks on basic mathematics, algebra, and calculus.
• Online Courses: Websites like Coursera, Khan Academy, and edX offer courses on mathematical concepts.
• Educational Websites: Websites like Mathway, Wolfram Alpha, and Symbolab provide tools for mathematical calculations and comparisons.
• Tutoring: Consider working with a math tutor for personalized instruction and support.

10. FAQs About Comparison in Math

1. Why is comparing numbers important in our daily lives?
Comparing numbers is essential for various daily activities, such as comparing prices, temperatures, and distances, which helps us make informed decisions.

2. How is comparing numbers different from ordering numbers?
Comparing numbers involves determining whether one number is greater, smaller, or equal to another, while ordering numbers involves arranging them in ascending or descending order.

3. What is the quick way for comparing numbers?
A quick way to compare numbers is to use a number line and mark the numbers to visually assess their relative positions.

4. What do you call it when you compare two numbers?
When you compare two numbers, it is called a numerical comparison, which involves determining their relative magnitude using symbols like >, <, or =.

5. How do you teach comparing numbers?
To teach comparing numbers, start with concrete examples, use visual aids like number lines, and gradually introduce symbols and methods for comparing different types of numbers.

6. What is the easiest way to compare fractions?
The easiest way to compare fractions is to convert them to equivalent fractions with a common denominator and then compare the numerators.

Conclusion

What does compare mean in math terms is a fundamental skill that enables us to analyze, interpret, and make informed decisions based on numerical and mathematical relationships. Understanding the different methods for comparing numbers, using mathematical symbols correctly, and avoiding common mistakes can enhance your accuracy and confidence in mathematical problem-solving. Whether it’s comparing prices, analyzing data, or optimizing processes, the ability to compare effectively is essential in both academic and real-world contexts.

Are you struggling to compare different options and make informed decisions? Visit COMPARE.EDU.VN today! Our comprehensive comparison tools provide detailed analyses and objective evaluations to help you make the best choices. Whether you’re a student, consumer, or professional, COMPARE.EDU.VN is your go-to resource for clear, concise, and accurate comparisons.

Contact us:

Address: 333 Comparison Plaza, Choice City, CA 90210, United States
WhatsApp: +1 (626) 555-9090
Website: compare.edu.vn