Comparing two unlike fractions can seem daunting, but it’s a crucial skill in mathematics and everyday life. How To Compare Two Unlike Fractions? By finding a common denominator, converting fractions to decimals, or using cross-multiplication. COMPARE.EDU.VN offers in-depth explanations and visual aids to simplify the comparison process, ensuring you master the art of fraction comparison. Whether you’re a student tackling homework or an adult using fractions in cooking or budgeting, understanding fraction comparison will empower you to make informed decisions and solve problems with ease, boosting your math proficiency and problem-solving confidence.
1. Understanding the Basics of Fractions
Before diving into how to compare two unlike fractions, let’s solidify our understanding of what fractions are and their components. A fraction represents a part of a whole and is composed of two main parts: the numerator and the denominator. The numerator indicates the number of parts we have, while the denominator specifies the total number of equal parts that make up the whole. For instance, in the fraction 3/4, 3 is the numerator, and 4 is the denominator.
1.1 Numerator and Denominator Explained
The numerator is the number above the fraction bar, representing how many parts of the whole you are considering. The denominator is the number below the fraction bar, indicating the total number of equal parts the whole is divided into. For example, if you have a pizza cut into 8 slices and you eat 3 slices, the fraction representing the amount you ate is 3/8. Here, 3 (the number of slices you ate) is the numerator, and 8 (the total number of slices) is the denominator.
1.2 Types of Fractions
Fractions come in various forms, each with its own characteristics:
- Proper Fractions: These are fractions where the numerator is less than the denominator, such as 1/2, 3/4, and 5/8. Proper fractions represent a value less than one.
- Improper Fractions: These are fractions where the numerator is greater than or equal to the denominator, such as 5/3, 7/4, and 8/8. Improper fractions represent a value greater than or equal to one.
- Mixed Numbers: These combine a whole number and a proper fraction, such as 1 1/2, 2 3/4, and 3 1/8. Mixed numbers are another way to represent values greater than one.
Understanding these basic concepts is crucial before learning how to compare two unlike fractions.
2. Why Comparing Unlike Fractions Can Be Challenging
Comparing fractions becomes tricky when they have different denominators. This is because the denominators tell us the size of the pieces we’re dealing with. If the pieces are different sizes, it’s hard to tell which fraction represents a larger portion of the whole. This section delves into why it’s challenging and sets the stage for learning effective comparison methods.
2.1 Understanding the Challenge of Different Denominators
When fractions have different denominators, it’s like comparing apples and oranges. For instance, consider the fractions 1/3 and 1/4. Here, 1/3 means one part out of three equal parts, while 1/4 means one part out of four equal parts. Since the sizes of the parts (thirds and fourths) are different, it’s not immediately clear which fraction is larger. Without a common base, direct comparison is difficult, which is why understanding how to compare two unlike fractions is so important.
2.2 The Need for a Common Base for Comparison
To accurately compare fractions with different denominators, you need to convert them into fractions with a common denominator. This process involves finding a common multiple of the denominators and adjusting the numerators accordingly. Once the fractions have the same denominator, you can easily compare them by looking at their numerators. This transformation ensures that you are comparing like parts, making the comparison accurate and straightforward.
3. Method 1: Finding a Common Denominator
One of the most reliable methods for how to compare two unlike fractions is to find a common denominator. This involves identifying a common multiple of the denominators of the fractions you want to compare. Once you have a common denominator, you can adjust the numerators and directly compare the fractions.
3.1 Identifying the Least Common Multiple (LCM)
The first step in this method is to find the Least Common Multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators. You can find the LCM by listing the multiples of each denominator until you find a common multiple.
For example, let’s compare 2/3 and 3/4. The denominators are 3 and 4. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The multiples of 4 are 4, 8, 12, 16, 20, and so on. The smallest common multiple of 3 and 4 is 12. Therefore, the LCM of 3 and 4 is 12.
3.2 Converting Fractions to Equivalent Fractions with the LCM as the Denominator
Once you’ve found the LCM, the next step is to convert each fraction into an equivalent fraction with the LCM as the denominator. To do this, you multiply both the numerator and the denominator of each fraction by a number that will make the denominator equal to the LCM.
For 2/3, you need to multiply the denominator 3 by 4 to get 12. So, you also multiply the numerator 2 by 4:
[
frac{2}{3} times frac{4}{4} = frac{8}{12}
]
For 3/4, you need to multiply the denominator 4 by 3 to get 12. So, you also multiply the numerator 3 by 3:
[
frac{3}{4} times frac{3}{3} = frac{9}{12}
]
Now you have two equivalent fractions: 8/12 and 9/12.
3.3 Comparing the Numerators
With the fractions now having a common denominator, you can easily compare them by looking at their numerators. The fraction with the larger numerator is the larger fraction.
In this case, you are comparing 8/12 and 9/12. Since 9 is greater than 8, 9/12 is greater than 8/12. Therefore, 3/4 is greater than 2/3.
This method provides a straightforward approach to how to compare two unlike fractions, ensuring accurate results by using a common base for comparison.
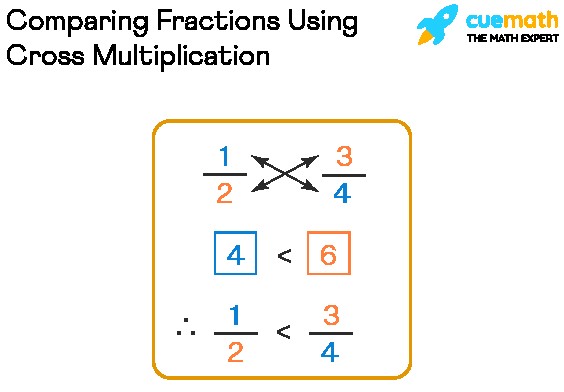
4. Method 2: Cross-Multiplication
Cross-multiplication is another effective method for how to compare two unlike fractions. This technique involves multiplying the numerator of one fraction by the denominator of the other fraction and then comparing the resulting products. It’s a quick and efficient way to determine which fraction is larger without explicitly finding a common denominator.
4.1 Understanding the Cross-Multiplication Technique
To use cross-multiplication, you multiply the numerator of the first fraction by the denominator of the second fraction, and then multiply the numerator of the second fraction by the denominator of the first fraction. The results are then compared to determine which fraction is larger.
4.2 Steps for Cross-Multiplication
Let’s illustrate this with an example: Compare 3/5 and 2/3.
Step 1: Multiply the numerator of the first fraction (3) by the denominator of the second fraction (3):
[
3 times 3 = 9
]
Step 2: Multiply the numerator of the second fraction (2) by the denominator of the first fraction (5):
[
2 times 5 = 10
]
Step 3: Compare the results. In this case, 9 and 10.
4.3 Interpreting the Results
The fraction corresponding to the larger product is the larger fraction. Since 10 is greater than 9, 2/3 is greater than 3/5.
Therefore, 2/3 > 3/5.
This method offers a straightforward shortcut to how to compare two unlike fractions, especially useful when quick comparisons are needed.
5. Method 3: Converting Fractions to Decimals
Converting fractions to decimals is a straightforward method for how to compare two unlike fractions. This approach involves dividing the numerator by the denominator to obtain the decimal equivalent of each fraction. Once you have the decimal values, you can easily compare them to determine which fraction is larger.
5.1 Dividing Numerator by Denominator
To convert a fraction to a decimal, divide the numerator by the denominator. For example, to convert 3/4 to a decimal, you would divide 3 by 4:
[
frac{3}{4} = 3 div 4 = 0.75
]
Similarly, to convert 5/8 to a decimal, you would divide 5 by 8:
[
frac{5}{8} = 5 div 8 = 0.625
]
5.2 Comparing Decimal Values
Once you have the decimal values for each fraction, you can easily compare them. The fraction with the larger decimal value is the larger fraction.
Using the previous examples, you have:
- 3/4 = 0.75
- 5/8 = 0.625
Comparing 0.75 and 0.625, you can see that 0.75 is greater than 0.625.
5.3 Advantages and Disadvantages of This Method
Advantages:
- Simplicity: Converting fractions to decimals is a straightforward process that many people find easy to understand.
- Ease of Comparison: Decimals are easy to compare, especially when using a calculator.
Disadvantages:
- Decimal Repetition: Some fractions result in repeating decimals, which can make comparison more difficult.
- Rounding Errors: Rounding decimals can introduce slight inaccuracies, especially if you need to compare fractions with very close values.
Despite these potential drawbacks, converting fractions to decimals remains a practical method for how to compare two unlike fractions, particularly when accuracy is not extremely critical.
6. Method 4: Visual Comparison with Diagrams
Visual comparison using diagrams is a highly intuitive method for how to compare two unlike fractions. This approach involves representing fractions as parts of a whole using visual aids like pie charts, bar models, or number lines. By visually comparing the fractional parts, you can quickly determine which fraction is larger.
6.1 Using Pie Charts to Represent Fractions
Pie charts are excellent tools for visualizing fractions. Each fraction can be represented as a slice of a pie, where the size of the slice corresponds to the fraction’s value. To compare fractions, you simply compare the sizes of the slices.
For example, to compare 1/3 and 1/4, you would draw two pie charts. Divide one pie chart into three equal slices, and shade one slice to represent 1/3. Divide the other pie chart into four equal slices, and shade one slice to represent 1/4. By visually comparing the shaded areas, you can easily see that 1/3 is larger than 1/4.
6.2 Bar Models for Fraction Comparison
Bar models are another effective visual tool for how to compare two unlike fractions. These models use rectangular bars to represent the whole, which is then divided into equal parts according to the denominator of the fraction.
To compare 2/5 and 3/8, you would draw two bars of equal length. Divide the first bar into five equal parts and shade two parts to represent 2/5. Divide the second bar into eight equal parts and shade three parts to represent 3/8. By comparing the shaded lengths, you can visually determine which fraction is larger.
6.3 Number Lines for Visualizing Fractions
Number lines can also be used to compare fractions. Draw a number line and mark the positions of the fractions you want to compare. The fraction that lies further to the right on the number line is the larger fraction.
For instance, to compare 1/2 and 2/3, you would draw a number line from 0 to 1. Divide the number line into segments that correspond to the fractions’ denominators (in this case, sixths would work well). Mark 1/2 (which is 3/6) and 2/3 (which is 4/6) on the number line. Since 2/3 is to the right of 1/2, you can conclude that 2/3 is larger than 1/2.
Using diagrams provides a clear and intuitive understanding of how to compare two unlike fractions, making it easier to grasp the concept, especially for visual learners.
7. Special Cases and Simplifications
While the methods discussed so far are generally applicable, certain special cases allow for quicker and more intuitive comparisons. Recognizing these scenarios can save time and effort when you how to compare two unlike fractions.
7.1 Comparing Fractions with the Same Numerator
When two fractions have the same numerator, the fraction with the smaller denominator is the larger fraction. This is because if you divide something into fewer parts, each part will be larger.
For example, compare 2/5 and 2/7. Both fractions have the same numerator (2). Since 5 is smaller than 7, 2/5 is larger than 2/7. This can be understood visually: if you have two slices of a pie, you get more if the pie is cut into only five slices rather than seven.
7.2 Comparing Fractions to 1/2
Another useful simplification is to compare fractions to 1/2. If one fraction is greater than 1/2 and the other is less than 1/2, the comparison is straightforward.
For example, compare 3/5 and 2/7. To determine how to compare two unlike fractions, note that 3/5 is greater than 1/2 (since 3 is more than half of 5), and 2/7 is less than 1/2 (since 2 is less than half of 7). Therefore, 3/5 is larger than 2/7.
7.3 Using Benchmarks (0, 1/4, 3/4, 1) for Quick Estimation
Using benchmark fractions like 0, 1/4, 3/4, and 1 can provide quick estimations and facilitate comparisons. For example, if one fraction is close to 1 and another is close to 0, the comparison is immediately clear.
Consider comparing 7/8 and 1/5. Here, 7/8 is very close to 1, and 1/5 is very close to 0. Therefore, 7/8 is much larger than 1/5. Similarly, if one fraction is slightly above 1/4 and another is significantly below 1/4, you can make a quick judgment without needing precise calculations.
Understanding these special cases and simplifications provides additional tools for how to compare two unlike fractions efficiently and accurately.
8. Real-World Applications of Comparing Fractions
Comparing fractions is not just a theoretical exercise; it has numerous practical applications in everyday life. Understanding how to compare two unlike fractions can help you make informed decisions in various situations.
8.1 Cooking and Baking
In cooking and baking, recipes often require comparing fractional amounts of ingredients. For example, you might need to determine whether 2/3 cup of flour is more or less than 3/5 cup of sugar. Accurately comparing these fractions ensures that your recipes turn out as expected. If a recipe calls for 1/4 teaspoon of salt and another suggests 2/8 teaspoon, knowing that 2/8 simplifies to 1/4 allows you to measure the correct amount without confusion.
8.2 Shopping and Discounts
Comparing fractions is also useful when evaluating discounts. For instance, if one store offers 1/3 off an item and another offers 2/5 off the same item, knowing how to compare these fractions helps you determine which discount is better. If you’re comparing deals where one offers 1/4 off and another offers 3/10 off, understanding that 1/4 is 2.5/10 helps you quickly see that 3/10 is the better deal.
8.3 Measuring and Construction
In measuring and construction, fractions are commonly used. Whether you’re measuring lumber, fabric, or paint, being able to compare fractions is essential for accurate results. For example, if you need a piece of wood that is at least 3/4 inch thick and you have a piece that is 5/8 inch thick, knowing how to compare these fractions helps you determine if the piece is thick enough.
8.4 Financial Planning and Budgeting
Fractions play a role in financial planning and budgeting as well. For instance, you might need to compare the fraction of your income spent on housing versus transportation. Understanding how to compare two unlike fractions can help you make informed decisions about where to allocate your resources. If you’re trying to save money and one area takes 1/5 of your income while another takes 2/7, comparing those fractions can highlight where you might cut back.
These real-world applications demonstrate the importance of mastering how to compare two unlike fractions. Whether you’re in the kitchen, at the store, or managing your finances, this skill is a valuable asset.
9. Common Mistakes to Avoid
When learning how to compare two unlike fractions, it’s common to encounter certain pitfalls. Being aware of these common mistakes can help you avoid errors and ensure accurate comparisons.
9.1 Incorrectly Comparing Numerators Without a Common Denominator
One of the most frequent errors is comparing numerators without first ensuring that the fractions have a common denominator. For instance, incorrectly assuming that 1/3 is greater than 1/4 simply because 1 is less than 4. The denominators must be the same before the numerators can be accurately compared. Always find a common denominator before making a comparison based on the numerators.
9.2 Misapplying Cross-Multiplication
Cross-multiplication is a useful shortcut, but it must be applied correctly. A common mistake is multiplying the wrong pairs of numbers or misinterpreting the results. Remember to multiply the numerator of the first fraction by the denominator of the second fraction and vice versa. Ensure that you correctly associate the resulting products with their respective fractions to determine which one is larger.
9.3 Rounding Decimals Prematurely
When converting fractions to decimals, rounding prematurely can lead to inaccuracies, especially if the decimals are very close. For example, if you’re comparing 0.6666… and 0.6667, rounding both to 0.67 will lead to the incorrect conclusion that they are equal. Always carry out the decimal division to a sufficient number of decimal places before rounding, or avoid rounding altogether if precise comparison is needed.
9.4 Neglecting Simplification
Failing to simplify fractions before comparing them can also lead to errors. Simplifying fractions to their lowest terms makes the comparison easier and reduces the risk of mistakes. For example, comparing 4/8 and 2/5 is more complex than comparing 1/2 and 2/5. Simplifying first can make the comparison more straightforward and accurate.
Avoiding these common mistakes will help you master how to compare two unlike fractions with confidence and precision.
10. Practice Problems and Solutions
To solidify your understanding of how to compare two unlike fractions, let’s work through some practice problems with detailed solutions.
Problem 1: Compare 3/4 and 5/7.
Solution:
Method 1: Finding a Common Denominator
- Find the LCM of 4 and 7. The LCM is 28.
- Convert both fractions to have a denominator of 28:
- 3/4 = (3 7) / (4 7) = 21/28
- 5/7 = (5 4) / (7 4) = 20/28
- Compare the numerators: 21/28 > 20/28.
- Therefore, 3/4 > 5/7.
Method 2: Cross-Multiplication
- Multiply 3 * 7 = 21
- Multiply 5 * 4 = 20
- Compare the results: 21 > 20
- Therefore, 3/4 > 5/7.
Problem 2: Compare 2/5 and 3/8.
Solution:
Method 1: Finding a Common Denominator
- Find the LCM of 5 and 8. The LCM is 40.
- Convert both fractions to have a denominator of 40:
- 2/5 = (2 8) / (5 8) = 16/40
- 3/8 = (3 5) / (8 5) = 15/40
- Compare the numerators: 16/40 > 15/40.
- Therefore, 2/5 > 3/8.
Method 2: Converting to Decimals
- Convert both fractions to decimals:
- 2/5 = 0.4
- 3/8 = 0.375
- Compare the decimal values: 0.4 > 0.375
- Therefore, 2/5 > 3/8.
Problem 3: Compare 4/9 and 1/2.
Solution:
Method 1: Finding a Common Denominator
- Find the LCM of 9 and 2. The LCM is 18.
- Convert both fractions to have a denominator of 18:
- 4/9 = (4 2) / (9 2) = 8/18
- 1/2 = (1 9) / (2 9) = 9/18
- Compare the numerators: 8/18 < 9/18.
- Therefore, 4/9 < 1/2.
Problem 4: Compare 5/6 and 7/9.
Solution:
Method 1: Finding a Common Denominator
- Find the LCM of 6 and 9. The LCM is 18.
- Convert both fractions to have a denominator of 18:
- 5/6 = (5 3) / (6 3) = 15/18
- 7/9 = (7 2) / (9 2) = 14/18
- Compare the numerators: 15/18 > 14/18.
- Therefore, 5/6 > 7/9.
These practice problems and solutions provide a comprehensive understanding of how to compare two unlike fractions using various methods.
FAQ: Mastering Fraction Comparisons
What does comparing fractions mean?
Comparing fractions means determining which of two or more fractions is larger or smaller in value.
Why is it important to know how to compare two unlike fractions?
Knowing how to compare two unlike fractions is crucial for various real-life applications, such as cooking, shopping, measuring, and financial planning.
What is the easiest method for how to compare two unlike fractions?
The easiest method depends on the individual. Some find converting to decimals straightforward, while others prefer finding a common denominator. Visual methods can also be very intuitive.
What if the denominators are very large?
If the denominators are very large, converting to decimals might be more practical. Alternatively, look for common factors to simplify the fractions before finding a common denominator.
Can I use a calculator to compare fractions?
Yes, calculators can be used to convert fractions to decimals or simplify them, making comparisons easier.
How does COMPARE.EDU.VN help in comparing fractions?
COMPARE.EDU.VN offers comprehensive guides and tools that simplify the process of comparing fractions. It provides step-by-step instructions, visual aids, and practical examples to help users master this essential skill.
Make Informed Decisions with COMPARE.EDU.VN
Mastering how to compare two unlike fractions is more than just an academic exercise; it’s a practical skill that empowers you to make informed decisions in various aspects of life. Whether you’re a student, a professional, or simply someone who wants to improve their everyday math skills, understanding fraction comparison is invaluable.
At COMPARE.EDU.VN, we recognize the importance of clear, concise, and reliable information. That’s why we’ve created a comprehensive guide to help you master the art of comparing fractions. But that’s not all we offer. Our website is dedicated to providing detailed and objective comparisons across a wide range of topics, ensuring you have the knowledge you need to make the best choices.
Are you struggling to decide between two products, services, or ideas? Do you want to weigh the pros and cons before making a purchase or investment? COMPARE.EDU.VN is here to help. Our platform offers side-by-side comparisons, expert reviews, and user feedback, making it easier than ever to evaluate your options and make confident decisions.
Don’t let confusion and uncertainty hold you back. Visit COMPARE.EDU.VN today and discover how our comprehensive comparisons can simplify your decision-making process. Whether you’re comparing fractions, choosing a new gadget, or evaluating different financial products, we’re here to provide the clarity you need.
Visit us at compare.edu.vn and start making smarter choices today Contact us at: 333 Comparison Plaza, Choice City, CA 90210, United States. Whatsapp: +1 (626) 555-9090.