Comparing two fractions with different denominators involves finding a common denominator to accurately determine which fraction is larger, smaller, or if they are equivalent; let COMPARE.EDU.VN show you how. By understanding the methods of comparing fractions with different denominators and utilizing tools like finding the least common multiple, you can confidently compare numerical fractions and fractional values. This guide will discuss comparing unlike fractions, comparing rational numbers, and determining inequality of fractions.
1. Understanding the Basics of Fractions
Before diving into comparing fractions with different denominators, it’s important to understand what fractions are and their components. A fraction represents a part of a whole and is composed of two main parts: the numerator and the denominator.
- Numerator: The number above the fraction bar represents the number of parts we have.
- Denominator: The number below the fraction bar represents the total number of equal parts that make up the whole.
For example, in the fraction 3/4, the numerator is 3, and the denominator is 4. This means we have 3 parts out of a total of 4 equal parts.
1.1. Types of Fractions
Understanding different types of fractions is crucial for comparing them effectively. Here are the main types:
- Proper Fractions: A proper fraction is one where the numerator is less than the denominator (e.g., 1/2, 3/4, 2/5).
- Improper Fractions: An improper fraction is one where the numerator is greater than or equal to the denominator (e.g., 5/3, 7/4, 8/8).
- Mixed Numbers: A mixed number is a combination of a whole number and a proper fraction (e.g., 1 1/2, 2 3/4, 3 1/5).
When comparing fractions, it may be necessary to convert improper fractions to mixed numbers or vice versa to make the comparison easier.
2. Identifying the Challenge: Different Denominators
The main challenge in comparing two fractions arises when they have different denominators. It’s difficult to directly compare fractions like 1/2 and 1/3 because they represent parts of different wholes. To overcome this, we need to find a common denominator, which allows us to compare the fractions on equal terms.
2.1. Why a Common Denominator is Important
A common denominator provides a standardized unit for comparing fractions. By expressing fractions with the same denominator, we can easily compare their numerators to determine which fraction is larger or smaller. For instance, if we convert 1/2 and 1/3 to fractions with a common denominator of 6, we get 3/6 and 2/6, respectively. Now, it’s clear that 3/6 (or 1/2) is greater than 2/6 (or 1/3).
3. Method 1: Finding the Least Common Multiple (LCM)
The most common and efficient method to compare fractions with different denominators is to find the Least Common Multiple (LCM) of the denominators. The LCM is the smallest multiple that is common to both denominators.
3.1. Steps to Find the LCM
- List the Multiples: List the multiples of each denominator.
- Identify Common Multiples: Look for multiples that are common to both lists.
- Find the Least Common Multiple: Identify the smallest common multiple.
Example: Find the LCM of 4 and 6.
- Multiples of 4: 4, 8, 12, 16, 20, 24, …
- Multiples of 6: 6, 12, 18, 24, 30, …
The common multiples are 12, 24, … The least common multiple (LCM) is 12.
3.2. Converting Fractions to Equivalent Fractions with the LCM
Once you have the LCM, convert each fraction to an equivalent fraction with the LCM as the new denominator. To do this, divide the LCM by the original denominator and multiply both the numerator and the denominator by the result.
Example: Convert 1/4 and 1/6 to equivalent fractions with a denominator of 12.
- For 1/4: Divide 12 by 4, which equals 3. Multiply both the numerator and denominator of 1/4 by 3 to get (1 3) / (4 3) = 3/12.
- For 1/6: Divide 12 by 6, which equals 2. Multiply both the numerator and denominator of 1/6 by 2 to get (1 2) / (6 2) = 2/12.
Now you can easily compare 3/12 and 2/12.
3.3. Comparing the Fractions
After converting the fractions to equivalent fractions with the same denominator, simply compare the numerators. The fraction with the larger numerator is the larger fraction.
Example: Comparing 3/12 and 2/12.
Since 3 is greater than 2, 3/12 > 2/12. Therefore, 1/4 > 1/6.
3.4. Examples of Comparing Fractions Using LCM
Example 1: Compare 2/5 and 3/7.
- Find the LCM of 5 and 7:
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, …
- Multiples of 7: 7, 14, 21, 28, 35, 42, …
- The LCM of 5 and 7 is 35.
- Convert the fractions to equivalent fractions with a denominator of 35:
- 2/5 = (2 7) / (5 7) = 14/35
- 3/7 = (3 5) / (7 5) = 15/35
- Compare the numerators:
- 14/35 and 15/35
- Since 15 > 14, 15/35 > 14/35.
- Conclusion:
- Therefore, 3/7 > 2/5.
Example 2: Compare 5/8 and 7/12.
- Find the LCM of 8 and 12:
- Multiples of 8: 8, 16, 24, 32, 40, 48, …
- Multiples of 12: 12, 24, 36, 48, 60, …
- The LCM of 8 and 12 is 24.
- Convert the fractions to equivalent fractions with a denominator of 24:
- 5/8 = (5 3) / (8 3) = 15/24
- 7/12 = (7 2) / (12 2) = 14/24
- Compare the numerators:
- 15/24 and 14/24
- Since 15 > 14, 15/24 > 14/24.
- Conclusion:
- Therefore, 5/8 > 7/12.
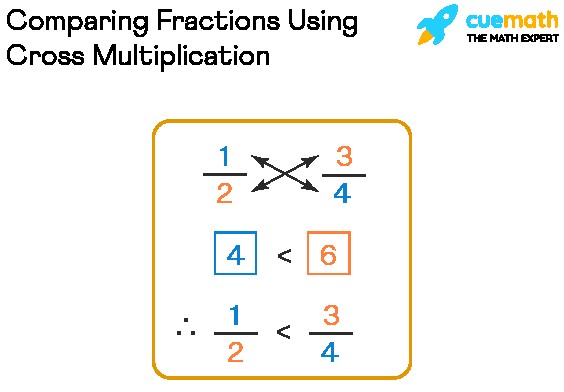
4. Method 2: Cross Multiplication
Another effective method for comparing two fractions with different denominators is cross multiplication. This method is quick and doesn’t require explicitly finding the LCM.
4.1. Steps for Cross Multiplication
- Cross Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction. Then, multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the Products: Compare the products obtained in step 1. The fraction corresponding to the larger product is the larger fraction.
Example: Compare 2/3 and 3/4 using cross multiplication.
- Cross Multiply:
- 2 * 4 = 8
- 3 * 3 = 9
- Compare the Products:
- Since 9 > 8, 3/4 > 2/3.
4.2. Understanding Why Cross Multiplication Works
Cross multiplication works because it is essentially a shortcut for finding a common denominator and comparing the numerators. When you cross multiply, you are implicitly multiplying each fraction by a form of 1 that makes the denominators the same.
For example, to compare a/b and c/d, cross multiplication involves comparing a*d and b*c. This is equivalent to comparing (a*d)/(b*d) and (b*c)/(b*d), which are the equivalent fractions with a common denominator of b*d.
4.3. Examples of Comparing Fractions Using Cross Multiplication
Example 1: Compare 3/5 and 4/7.
- Cross Multiply:
- 3 * 7 = 21
- 4 * 5 = 20
- Compare the Products:
- Since 21 > 20, 3/5 > 4/7.
Example 2: Compare 5/9 and 2/4.
- Cross Multiply:
- 5 * 4 = 20
- 2 * 9 = 18
- Compare the Products:
- Since 20 > 18, 5/9 > 2/4.
5. Method 3: Converting Fractions to Decimals
Another straightforward method to compare fractions with different denominators is to convert each fraction to its decimal equivalent. This method is particularly useful when dealing with complex fractions or when a calculator is available.
5.1. Steps to Convert Fractions to Decimals
- Divide Numerator by Denominator: Divide the numerator of each fraction by its denominator.
- Compare the Decimal Values: Compare the resulting decimal values. The fraction with the larger decimal value is the larger fraction.
Example: Compare 3/8 and 5/12.
- Convert to Decimals:
- 3/8 = 0.375
- 5/12 = 0.4166…
- Compare the Decimal Values:
- Since 0.4166… > 0.375, 5/12 > 3/8.
5.2. Advantages and Disadvantages of Using Decimals
- Advantages:
- Simple and straightforward, especially with a calculator.
- Easy to compare multiple fractions at once.
- Disadvantages:
- Some fractions result in repeating decimals, which may require rounding and approximation.
- May not be as conceptually clear as finding a common denominator.
5.3. Examples of Comparing Fractions Using Decimal Conversion
Example 1: Compare 1/3 and 2/7.
- Convert to Decimals:
- 1/3 = 0.333…
- 2/7 = 0.2857…
- Compare the Decimal Values:
- Since 0.333… > 0.2857…, 1/3 > 2/7.
Example 2: Compare 4/5 and 7/9.
- Convert to Decimals:
- 4/5 = 0.8
- 7/9 = 0.777…
- Compare the Decimal Values:
- Since 0.8 > 0.777…, 4/5 > 7/9.
6. Method 4: Benchmarking
Benchmarking involves comparing fractions to common reference points or benchmarks to quickly estimate their relative sizes. Common benchmarks include 0, 1/2, and 1.
6.1. Using 0, 1/2, and 1 as Benchmarks
- Comparing to 0: If a fraction is close to 0, it means the numerator is much smaller than the denominator.
- Comparing to 1/2: If a fraction is close to 1/2, the numerator is approximately half of the denominator.
- Comparing to 1: If a fraction is close to 1, the numerator is close to the denominator.
Example: Compare 1/5 and 4/7.
- 1/5 is close to 0.
- 4/7 is greater than 1/2 (since 4 is more than half of 7).
Therefore, 4/7 > 1/5.
6.2. Steps to Use Benchmarking Effectively
- Identify the Benchmarks: Determine which benchmarks (0, 1/2, 1) are relevant to the fractions being compared.
- Compare Each Fraction to the Benchmarks: Assess whether each fraction is less than, equal to, or greater than the chosen benchmarks.
- Draw Conclusions: Based on the comparison to the benchmarks, determine the relative sizes of the fractions.
6.3. Examples of Comparing Fractions Using Benchmarking
Example 1: Compare 2/9 and 5/8.
- 2/9 is less than 1/2 (since 2 is less than half of 9).
- 5/8 is greater than 1/2 (since 5 is more than half of 8).
Therefore, 5/8 > 2/9.
Example 2: Compare 3/7 and 6/11.
- 3/7 is slightly less than 1/2 (since 3 is slightly less than half of 7).
- 6/11 is slightly more than 1/2 (since 6 is slightly more than half of 11).
Therefore, 6/11 > 3/7.
7. Special Cases and Considerations
7.1. Comparing More Than Two Fractions
When comparing more than two fractions with different denominators, it is best to find the LCM of all the denominators and convert each fraction to an equivalent fraction with the LCM as the denominator. This allows for a direct comparison of all the numerators.
Example: Compare 1/3, 2/5, and 3/8.
- Find the LCM of 3, 5, and 8:
- The LCM of 3, 5, and 8 is 120.
- Convert the fractions to equivalent fractions with a denominator of 120:
- 1/3 = (1 40) / (3 40) = 40/120
- 2/5 = (2 24) / (5 24) = 48/120
- 3/8 = (3 15) / (8 15) = 45/120
- Compare the numerators:
- 40/120, 48/120, and 45/120
- The order from least to greatest is 40/120 < 45/120 < 48/120.
- Conclusion:
- Therefore, 1/3 < 3/8 < 2/5.
7.2. Comparing Negative Fractions
When comparing negative fractions, remember that the fraction with the smaller absolute value is the larger fraction.
Example: Compare -1/4 and -1/3.
- Find the LCM of 4 and 3:
- The LCM of 4 and 3 is 12.
- Convert the fractions to equivalent fractions with a denominator of 12:
- -1/4 = (-1 3) / (4 3) = -3/12
- -1/3 = (-1 4) / (3 4) = -4/12
- Compare the numerators:
- -3/12 and -4/12
- Since -3 is greater than -4, -3/12 > -4/12.
- Conclusion:
- Therefore, -1/4 > -1/3.
7.3. Comparing Fractions Greater Than 1
When comparing fractions greater than 1 (improper fractions or mixed numbers), convert them to improper fractions or mixed numbers with common denominators, and then compare the numerators or whole number parts.
Example: Compare 1 1/2 and 5/3.
- Convert to improper fractions:
- 1 1/2 = 3/2
- Find the LCM of 2 and 3:
- The LCM of 2 and 3 is 6.
- Convert the fractions to equivalent fractions with a denominator of 6:
- 3/2 = (3 3) / (2 3) = 9/6
- 5/3 = (5 2) / (3 2) = 10/6
- Compare the numerators:
- 9/6 and 10/6
- Since 10 > 9, 10/6 > 9/6.
- Conclusion:
- Therefore, 5/3 > 1 1/2.
8. Real-World Applications
Comparing fractions is a fundamental skill with numerous real-world applications. Here are a few examples:
8.1. Cooking and Baking
In cooking and baking, recipes often involve fractions. Comparing fractions helps in adjusting ingredient quantities, determining the proportion of ingredients, and scaling recipes up or down.
Example: A recipe calls for 1/3 cup of flour and 1/4 cup of sugar. To determine which ingredient is used in greater quantity, you need to compare 1/3 and 1/4.
8.2. Measuring and Construction
In fields like construction and carpentry, accurate measurements are crucial. Comparing fractions is essential for cutting materials to the correct size, calculating dimensions, and ensuring precise construction.
Example: A carpenter needs to cut a piece of wood to be 5/8 of an inch thick. If they have another piece that is 7/16 of an inch thick, they need to compare 5/8 and 7/16 to determine which piece is thicker.
8.3. Finances and Budgeting
Comparing fractions is useful in managing finances and budgeting. It helps in calculating proportions, comparing expenses, and making informed financial decisions.
Example: If you allocate 1/5 of your budget to housing and 1/8 to transportation, comparing 1/5 and 1/8 helps you determine which category takes up a larger portion of your budget.
8.4. Time Management
In time management, comparing fractions helps in allocating time to different tasks, estimating the duration of activities, and prioritizing tasks effectively.
Example: If you spend 2/5 of your day working and 1/4 of your day on personal activities, comparing 2/5 and 1/4 helps you understand how your time is distributed.
9. Tips and Tricks for Mastering Fraction Comparison
9.1. Practice Regularly
The key to mastering fraction comparison is consistent practice. Work through various examples and exercises to reinforce your understanding of the different methods.
9.2. Visualize Fractions
Use visual aids like fraction bars, pie charts, or number lines to visualize fractions. This can help you develop a better intuition for their relative sizes.
9.3. Use Online Resources
Take advantage of online resources like educational websites, interactive tutorials, and practice quizzes to enhance your learning experience.
9.4. Seek Help When Needed
Don’t hesitate to seek help from teachers, tutors, or classmates if you’re struggling with fraction comparison. Clarifying your doubts and addressing your weaknesses will accelerate your learning progress.
9.5. Understand the Underlying Concepts
Focus on understanding the underlying concepts rather than just memorizing procedures. This will enable you to apply your knowledge to a wider range of problems and develop a deeper appreciation for mathematics.
10. Conclusion: Empowering Decision-Making with Fraction Comparison
In conclusion, comparing two fractions with different denominators is a vital skill with broad applications in mathematics and everyday life. By mastering methods like finding the LCM, cross multiplication, converting to decimals, and benchmarking, you can confidently compare fractions and make informed decisions. Whether you’re adjusting a recipe, measuring materials, managing finances, or allocating time, the ability to compare fractions accurately will empower you to solve problems and achieve your goals.
At COMPARE.EDU.VN, we understand the challenges and frustrations that come with comparing different options, whether it’s fractions or complex products and services. That’s why we’ve created a platform to provide you with detailed, objective comparisons to help you make confident decisions.
Are you struggling to choose between two products? Confused about which service best fits your needs? Visit COMPARE.EDU.VN today! Our comprehensive comparison guides offer clear, concise information, making your decision-making process easier and more efficient. Don’t let uncertainty hold you back – discover the power of informed choices with COMPARE.EDU.VN.
Feel free to contact us at:
Address: 333 Comparison Plaza, Choice City, CA 90210, United States.
Whatsapp: +1 (626) 555-9090.
Website: compare.edu.vn
11. FAQs About Comparing Fractions
11.1. Why is it Necessary to Find a Common Denominator When Comparing Fractions?
Finding a common denominator is essential because it provides a standardized unit for comparison. When fractions have the same denominator, you can directly compare their numerators to determine which fraction is larger or smaller.
11.2. What is the Least Common Multiple (LCM) and How Does It Help in Comparing Fractions?
The Least Common Multiple (LCM) is the smallest multiple that is common to two or more numbers. In the context of comparing fractions, finding the LCM of the denominators allows you to convert the fractions to equivalent fractions with the same denominator, making comparison straightforward.
11.3. Can You Explain the Cross-Multiplication Method for Comparing Fractions?
The cross-multiplication method involves multiplying the numerator of one fraction by the denominator of the other fraction and comparing the resulting products. This method is a shortcut for finding a common denominator and comparing numerators, making it a quick and efficient way to compare two fractions.
11.4. How Do You Convert a Fraction to a Decimal?
To convert a fraction to a decimal, divide the numerator by the denominator. The resulting decimal value represents the fraction in decimal form, which can then be easily compared to other decimals.
11.5. What are Benchmarks and How Can They Be Used to Compare Fractions?
Benchmarks are common reference points like 0, 1/2, and 1 that help in estimating the relative sizes of fractions. By comparing each fraction to these benchmarks, you can quickly determine their approximate values and compare them without finding a common denominator.
11.6. How Do You Compare More Than Two Fractions with Different Denominators?
To compare more than two fractions with different denominators, find the LCM of all the denominators and convert each fraction to an equivalent fraction with the LCM as the denominator. This allows for a direct comparison of all the numerators.
11.7. What Should You Do When Comparing Negative Fractions?
When comparing negative fractions, remember that the fraction with the smaller absolute value is the larger fraction. You can find a common denominator and compare the numerators, keeping in mind that smaller negative numbers are greater than larger negative numbers.
11.8. How Do You Compare Fractions Greater Than 1 (Improper Fractions or Mixed Numbers)?
When comparing fractions greater than 1, convert them to improper fractions or mixed numbers with common denominators. Then, compare the numerators or whole number parts to determine which fraction is larger.
11.9. What are Some Real-World Applications of Comparing Fractions?
Comparing fractions is used in cooking, measuring, construction, finance, time management, and various other fields. It helps in adjusting recipes, calculating dimensions, managing budgets, and allocating time effectively.
11.10. What are Some Tips for Mastering Fraction Comparison?
To master fraction comparison, practice regularly, visualize fractions, use online resources, seek help when needed, and focus on understanding the underlying concepts rather than just memorizing procedures.