How Do You Compare Numbers in Scientific Notation Effectively?

Comparing numbers in scientific notation can seem daunting, but it becomes straightforward with the right approach. At COMPARE.EDU.VN, we simplify this process, offering clear methods to determine which number is larger or smaller, along with comprehensive examples. Learn effective strategies for comparing and ordering scientific notation, and easily convert between standard and scientific notation.

1. Understanding Scientific Notation

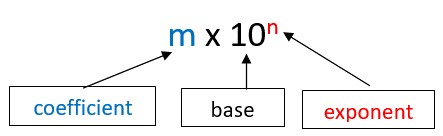
Before diving into comparisons, it’s crucial to understand the structure of scientific notation. Scientific notation is a way of expressing numbers as a product of two factors: a coefficient and a power of 10.

• The coefficient (m) is a number typically between 1 and 10 (1 ≤ |m| < 10).
• The exponent (n) is an integer, which can be positive, negative, or zero, representing the power of 10.

A number in scientific notation looks like this: m x 10ⁿ.

Examples of Numbers in Scientific Notation:

• 2.7 x 10⁴
• -8.2 x 10^-2
• 5.1274 x 10⁰
• 9 x 10¹⁵
• -8.7 x 10^-8

Examples of Numbers Not in Scientific Notation:

• 273 x 10⁷ (Coefficient is greater than 10)
• 0.7 x 10³ (Coefficient is less than 1)
• 8 x 2⁹ (Base needs to be 10, not 2)
• 7.328 x 1000 (Needs an exponent)
• -0.3 x 10^-2 (Coefficient is less than 1)

2. Comparing Positive Numbers in Scientific Notation

When comparing positive numbers in scientific notation, the exponent plays a crucial role. Here’s how to compare them effectively:

2.1. Comparing Exponents

The number with the larger exponent is the larger number. This rule applies whether the exponents are positive or negative. For instance, if b > d, then a x 10^b > c x 10^d.

Examples:

• 1.48 x 10³ is smaller than 4.82 x 10⁵ because 3 < 5.
• 3.02 x 10¹² is larger than 9.1 x 10⁸ because 12 > 8.
• 5.2 x 10^-2 is larger than 1.78 x 10^-4 because -2 > -4.
• 8.45 x 10^-2 is smaller than 2.8 x 10⁰ because -2 < 0.

2.2. Comparing Coefficients (When Exponents Are Equal)

If the exponents are the same, the number with the larger coefficient is the larger number.

Example:

• 3.2 x 10⁵ is larger than 2.9 x 10⁵ because 3.2 > 2.9.

3. Comparing Negative Numbers in Scientific Notation

When dealing with negative numbers, remember that the number closest to zero is the larger one. So, -2 is greater than -5.

3.1. Comparing Exponents

For negative numbers in scientific notation, the number with the smaller exponent is the larger number (less negative).

Examples:

• -1.48 x 10³ is larger than -4.82 x 10⁵ because 3 < 5 (less negative).
• -3.02 x 10¹² is smaller than -9.1 x 10⁸ because 12 > 8 (more negative).
• -5.2 x 10^-2 is smaller than -1.78 x 10^-4 because -2 > -4 (more negative).
• -8.45 x 10^-2 is larger than -2.8 x 10⁰ because -2 < 0 (less negative).

3.2. Comparing Coefficients (When Exponents Are Equal)

If the exponents are the same, the negative number with the smaller coefficient is the larger number.

Example:

• -3.2 x 10⁵ is smaller than -2.9 x 10⁵ because -3.2 < -2.9.

4. Comparing Positive and Negative Numbers in Scientific Notation

This is straightforward: any positive number is always greater than any negative number, regardless of their exponents or coefficients.

Examples:

• -2.6 x 10³ is smaller than 1.2 x 10².
• 5.8 x 10^-4 is larger than -7 x 10⁵.
• -2.6 x 10^-2 is smaller than 1.4 x 10^-8.

5. Comparing Numbers in Scientific Notation with Standard Notation

When comparing a number in scientific notation with a number in standard notation, you have two options:

1. Convert the number in scientific notation into standard notation.
2. Convert the number in standard notation into scientific notation.

The choice depends on your preference, but for very large or very small numbers, converting to scientific notation is often easier.

Examples:

• 3.4 x 10³ is larger than 3,000 because 3.4 x 10³ = 3.4 x 1000 = 3,400.
• 5.8 x 10^-2 is smaller than 0.06 because 5.8 x 10^-2 = 5.8 ÷ 100 = 0.058.
• 2.6 x 10⁹ is larger than 300,000,000 because 300,000,000 = 3 x 10⁸ (smaller exponent).

6. Worked Examples

Let’s walk through some examples to solidify your understanding.

6.1. Example 1: Comparing Two Positive Numbers

Question: Which is bigger: 4.8 x 10⁵ or 8.2 x 10³?

Solution:

• 4.8 x 10⁵ has an exponent of 5.
• 8.2 x 10³ has an exponent of 3.

Since 5 > 3, 4.8 x 10⁵ > 8.2 x 10³.

6.2. Example 2: Ordering Positive Numbers

Question: Put these three numbers in order from smallest to largest: 3.4 x 10^-1, 1.7 x 10¹, and 7.8 x 10^-2.

Solution:

• 3. 4 x 10^-1 has an exponent of -1.
• 5. 7 x 10¹ has an exponent of 1.
• 6. 8 x 10^-2 has an exponent of -2.

Ordering the exponents from smallest to largest: -2, -1, 1.

Therefore, the correct order is: 7.8 x 10^-2, 3.4 x 10^-1, and 1.7 x 10¹.

6.3. Example 3: Ordering Negative Numbers

Question: Put these three numbers in order from smallest to largest: -9.3 x 10^-1, -3.1 x 10⁶, and -2.5 x 10³.

Solution:

• -9.3 x 10^-1 has an exponent of -1.
• -3.1 x 10⁶ has an exponent of 6.
• -2.5 x 10³ has an exponent of 3.

Ordering the exponents from smallest to largest: -1, 3, 6.

For negative numbers, the smaller the absolute value (exponent), the larger the number.

So, the correct order from smallest to largest is: -3.1 x 10⁶, -2.5 x 10³, and -9.3 x 10^-1.

6.4. Example 4: Ordering Mixed Numbers (Positive and Negative)

Question: Put these three numbers in order from smallest to largest: 2.8 x 10^-2, -4 x 10^-3, and -6.5 x 10^-1.

Solution:

We have two negative numbers and one positive number. The positive number will always be the largest.

Let’s order the two negative numbers:

• -4 x 10^-3 has an exponent of -3.
• -6.5 x 10^-1 has an exponent of -1.

Since -3 < -1, -4 x 10^-3 is greater than -6.5 x 10^-1.

Therefore, the correct order from smallest to largest is: -6.5 x 10^-1, -4 x 10^-3, and 2.8 x 10^-2.

7. Useful Tips and Tricks

• Always Compare Exponents First: The exponent gives you the first indication of the number’s magnitude.
• Convert to Standard Notation: When in doubt, convert the numbers to standard notation to visualize their values more clearly.
• Remember Negative Number Rules: Keep in mind that with negative numbers, the smaller the absolute value, the larger the number.
• Use COMPARE.EDU.VN Resources: Take advantage of the various tools and examples available on COMPARE.EDU.VN to enhance your understanding.

8. The Importance of Scientific Notation

Scientific notation is not just an academic exercise; it’s a practical tool used across various fields:

• Science: Expressing incredibly small values such as the mass of an electron (approximately 9.11 × 10^-31 kg) or vast distances in space, like the distance to the Andromeda Galaxy (approximately 2.5 × 10⁶ light-years).
• Engineering: Handling values in electrical engineering or material science where values can be extremely large or minute.
• Computer Science: Representing memory capacity or processing speeds.
• Economics: Simplifying large numbers like national debts or GDP figures.

9. Scientific Notation in Real Life

Here’s how scientific notation simplifies complex numbers in everyday scenarios:

9.1. Astronomy

Astronomers use scientific notation to describe distances between celestial bodies. For example, the distance from Earth to the Sun is about 1.5 x 10¹¹ meters. This is far more manageable than writing 150,000,000,000 meters.

9.2. Biology

In biology, scientific notation is used to express the size of cells or microorganisms. A typical bacterium might have a diameter of 2 x 10^-6 meters.

9.3. Chemistry

Chemists use scientific notation to represent the number of atoms or molecules in a sample. For instance, one mole of a substance contains approximately 6.022 x 10²³ particles (Avogadro’s number).

9.4. Computer Technology

The storage capacity of computer hard drives is often expressed in scientific notation. A 1 terabyte (TB) hard drive can store about 1 x 10¹² bytes of data.

10. Common Mistakes to Avoid

• Forgetting the Rules for Negative Numbers: Ensure you remember that when dealing with negative numbers, the number closer to zero is always greater.
• Misinterpreting Exponents: Double-check the exponents to ensure they are correctly compared, especially when they are negative.
• Ignoring the Coefficient: Always consider the coefficient when exponents are the same.
• Skipping Conversion: If you’re struggling with scientific notation, converting to standard notation can often provide a clearer comparison.

11. Additional Resources and Worksheets

For further practice, here are some useful resources:

• Comparing 2 Numbers in Scientific Notation Worksheets: Practice comparing pairs of numbers, including positive and negative exponents.
• Ordering Numbers in Scientific Notation Worksheets: Order sets of numbers in scientific notation from smallest to largest.
• Ordering Numbers in Scientific Notation and Standard Notation Worksheets: Combine your skills by ordering numbers presented in both scientific and standard notation.
• Online Quizzes: Test your knowledge with interactive quizzes that provide instant feedback.

12. Tools for Converting and Comparing Scientific Notation

12.1. Scientific Notation Calculators

Online scientific notation calculators can quickly convert numbers between standard and scientific notation. These tools are invaluable for checking your work and handling complex conversions.

12.2. Number System Converters

Number system converters can help convert between binary, octal, hexadecimal, and decimal numbers, which can be useful in certain scientific and technical contexts.

13. Conclusion: Mastering Scientific Notation

Comparing numbers in scientific notation is a fundamental skill that simplifies dealing with very large and very small values. By understanding the basic principles, practicing with examples, and utilizing available resources, you can master this skill and apply it confidently in various fields.

Ready to simplify your decision-making process? Visit COMPARE.EDU.VN today for comprehensive comparisons and expert insights.

14. FAQs: Comparing Numbers in Scientific Notation

14.1. What is scientific notation?

Scientific notation expresses numbers as a product of a coefficient (between 1 and 10) and a power of 10.

14.2. How do you compare two positive numbers in scientific notation?

Compare the exponents first. The number with the larger exponent is larger. If exponents are equal, compare the coefficients.

14.3. How do you compare two negative numbers in scientific notation?

The number with the smaller exponent is larger (less negative). If exponents are equal, the number with the smaller coefficient is larger.

14.4. How do you compare a positive and a negative number in scientific notation?

Any positive number is always larger than any negative number.

14.5. What if the exponents are the same when comparing numbers in scientific notation?

Compare the coefficients. The number with the larger coefficient is the larger number.

14.6. Should I convert to standard notation before comparing?

It’s optional, but it can help visualize the numbers more clearly, especially if you find scientific notation confusing.

14.7. What are some real-world applications of scientific notation?

Astronomy, biology, chemistry, and computer science all use scientific notation to handle very large or small numbers.

14.8. How does COMPARE.EDU.VN help with understanding scientific notation?

COMPARE.EDU.VN offers comprehensive guides, examples, and tools to simplify comparisons and enhance understanding.

14.9. What’s the most common mistake when comparing negative numbers in scientific notation?

Forgetting that the number closer to zero is larger. Always consider the absolute value of the exponent.

14.10. Where can I find more practice worksheets?

Numerous websites offer free worksheets. Also, check the resources mentioned in this article for direct links.

For more insights and comparisons, visit us at COMPARE.EDU.VN. Our team is dedicated to providing you with the most accurate and comprehensive information available.

Contact Information:

• Address: 333 Comparison Plaza, Choice City, CA 90210, United States
• WhatsApp: +1 (626) 555-9090
• Website: compare.edu.vn