Lattice energy comparison of ionic compounds involves assessing factors like ionic charge and size; COMPARE.EDU.VN offers comprehensive comparisons to aid in your analysis. By evaluating these factors, you can understand the strength of ionic bonds. Explore COMPARE.EDU.VN for detailed comparisons and expert insights, with topics including Born-Haber cycle, Coulomb’s law and ionic radii to enhance your comprehension.
1. What Is Lattice Energy And Why Does It Matter?
Lattice energy is the energy required to separate one mole of an ionic solid into its gaseous ions. It matters because it’s a measure of the strength of the ionic bonds within the compound, influencing properties such as melting point, solubility, and hardness. High lattice energy signifies strong bonds and greater stability.
1.1 How Is Lattice Energy Defined?
Lattice energy (U) is defined as the change in enthalpy when one mole of a solid ionic compound is separated into gaseous ions to an infinite distance. This process is endothermic, meaning it requires energy input, so lattice energy values are always positive.
1.2 What Factors Influence Lattice Energy?
Lattice energy is primarily influenced by two main factors:
- Ionic Charge: Higher charges on the ions lead to greater attractive forces and thus higher lattice energy.
- Ionic Size: Smaller ionic radii result in shorter interionic distances, leading to stronger attractions and higher lattice energy.
According to a study by the University of California, Berkeley, increasing ionic charge leads to a more significant impact on lattice energy than decreasing ionic size, highlighting the dominance of charge in determining ionic bond strength.
1.3 Why Is Understanding Lattice Energy Important?
Understanding lattice energy is vital for several reasons:
- Predicting Physical Properties: It helps predict physical properties of ionic compounds such as melting points, hardness, and solubility.
- Understanding Chemical Reactions: It provides insights into the stability and reactivity of ionic compounds in chemical reactions.
- Designing Materials: It aids in designing new materials with specific properties by controlling the strength of ionic interactions.
- Industrial Applications: Lattice energy considerations are crucial in various industrial processes such as ceramics manufacturing, metallurgy, and the development of electrolytes for batteries.
2. What Are The Key Factors Affecting Lattice Energy?
The key factors affecting lattice energy are ionic charge, ionic size, and the arrangement of ions in the crystal lattice. These factors determine the strength of electrostatic attractions between ions, influencing the overall stability and properties of ionic compounds.
2.1 The Role Of Ionic Charge
The magnitude of ionic charge has a direct impact on lattice energy. Higher charges lead to stronger electrostatic attractions between the ions, resulting in greater lattice energy. For instance, compounds with divalent ions (like MgO) generally have higher lattice energies than those with monovalent ions (like NaCl).
2.2 The Impact Of Ionic Size
Ionic size affects the distance between ions in the crystal lattice. Smaller ions can pack more closely together, leading to stronger electrostatic attractions and higher lattice energy. The internuclear distance, ( r_0 ), which is the sum of the ionic radii, is inversely proportional to the lattice energy, as described by the equation:
( U propto frac{Q_1 Q_2}{r_0} )
2.3 How Does Crystal Structure Influence Lattice Energy?
The arrangement of ions in the crystal lattice, also known as the crystal structure, affects lattice energy by influencing the Madelung constant. This constant accounts for the cumulative electrostatic interactions of all ions in the lattice. Different crystal structures, such as sodium chloride (NaCl) or cesium chloride (CsCl), have different Madelung constants, thus impacting the overall lattice energy.
2.4 What Is The Born-Mayer Equation?
The Born-Mayer equation is a more refined model for calculating lattice energy, taking into account repulsive forces between electron clouds of adjacent ions. The equation is:
( U = – frac{N_A M z_1 z_2 e^2}{4 pi epsilon_0 r_0} (1 – frac{n}{r_0}) )
Where:
- ( N_A ) is Avogadro’s number
- ( M ) is the Madelung constant
- ( z_1 ) and ( z_2 ) are the ion charges
- ( e ) is the elementary charge
- ( epsilon_0 ) is the vacuum permittivity
- ( r_0 ) is the shortest interionic distance
- ( n ) is the Born exponent
The Born-Mayer equation provides a more accurate estimation of lattice energy by considering repulsive forces, making it superior to simpler models.
3. What Methods Are Used To Determine Lattice Energy?
Methods to determine lattice energy include the Born-Haber cycle, calculations using the Born-Mayer equation, and experimental techniques like calorimetry. The Born-Haber cycle uses Hess’s law to relate lattice energy to other thermodynamic properties, while the Born-Mayer equation calculates it based on crystal structure and ionic properties.
3.1 Explain The Born-Haber Cycle
The Born-Haber cycle is a thermodynamic cycle used to calculate the lattice energy of an ionic compound. It applies Hess’s Law to relate the lattice energy to other energetic terms in the formation of an ionic compound. The steps in the cycle typically include:
- Sublimation Energy (( Delta H_{sub} )): Energy required to convert one mole of a solid element into gaseous atoms.
- Ionization Energy (( IE )): Energy required to remove an electron from a gaseous atom to form a gaseous cation.
- Dissociation Energy (( Delta H_{diss} )): Energy required to break one mole of bonds in a diatomic molecule into gaseous atoms.
- Electron Affinity (( EA )): Energy released when a gaseous atom gains an electron to form a gaseous anion.
- Heat of Formation (( Delta H_f )): Energy change when one mole of the compound is formed from its elements in their standard states.
The lattice energy (( U )) can be calculated using the following equation derived from Hess’s Law:
( Delta Hf = Delta H{sub} + IE + frac{1}{2} Delta H_{diss} + EA – U )
Rearranging for ( U ):
( U = Delta H{sub} + IE + frac{1}{2} Delta H{diss} + EA – Delta H_f )
The Born-Haber cycle is crucial because it provides an indirect experimental method to determine lattice energies, which are difficult to measure directly.
3.2 How Is Lattice Energy Calculated Using The Born-Mayer Equation?
The Born-Mayer equation is used to theoretically calculate lattice energy based on the crystal structure and ionic properties of the compound:
( U = – frac{N_A M z_1 z_2 e^2}{4 pi epsilon_0 r_0} (1 – frac{n}{r_0}) )
Where:
- ( N_A ) is Avogadro’s number
- ( M ) is the Madelung constant
- ( z_1 ) and ( z_2 ) are the ion charges
- ( e ) is the elementary charge
- ( epsilon_0 ) is the vacuum permittivity
- ( r_0 ) is the shortest interionic distance
- ( n ) is the Born exponent
This equation accounts for both attractive and repulsive forces between ions, providing a more accurate estimation of lattice energy compared to simpler models.
3.3 What Are Experimental Techniques For Measuring Lattice Energy?
Experimental techniques for measuring lattice energy are limited because lattice energy cannot be directly measured. However, it can be indirectly determined through a combination of experimental measurements and thermodynamic cycles like the Born-Haber cycle. Key experimental techniques include:
- Calorimetry: Measures the heat of formation (( Delta H_f )) of the ionic compound.
- Spectroscopy: Determines bond dissociation energies and ionization energies.
- X-ray Diffraction: Determines crystal structure and interionic distances.
These experimental data are then used in conjunction with the Born-Haber cycle to calculate the lattice energy.
3.4 How Do Different Methods Compare In Accuracy And Complexity?
| Method | Accuracy | Complexity | Data Required |
|---|---|---|---|
| Born-Haber Cycle | Moderate to High | Moderate | Heat of formation, sublimation energy, ionization energy, dissociation energy, electron affinity |
| Born-Mayer Equation | Moderate | High | Madelung constant, ionic charges, interionic distance, Born exponent |
| Experimental | High (when combined with Born-Haber) | High (requires multiple experimental techniques and careful data analysis) | Calorimetric data, spectroscopic data, X-ray diffraction data, and their integration within the Born-Haber cycle |

The Born-Haber cycle, when combined with experimental data, provides the most accurate estimation of lattice energy. The Born-Mayer equation is useful for theoretical calculations but relies on accurate knowledge of the crystal structure and ionic properties.
4. How To Compare Lattice Energies Of Different Ionic Compounds
To compare lattice energies of different ionic compounds, assess the ionic charges and sizes. Higher charges and smaller sizes generally indicate higher lattice energies due to stronger electrostatic attractions. Use the formula ( U propto frac{Q_1 Q_2}{r_0} ) as a guide, where ( Q_1 ) and ( Q_2 ) are the ionic charges and ( r_0 ) is the interionic distance.
4.1 Step-By-Step Guide To Comparing Lattice Energies
- Identify the Ionic Charges: Determine the charges of the cation and anion in each compound.
- Determine the Ionic Sizes: Find the ionic radii of the cation and anion for each compound.
- Calculate the Interionic Distance (( r_0 )): Sum the ionic radii of the cation and anion for each compound (( r0 = r+ + r_- )).
- Apply the Lattice Energy Relationship: Use the relationship ( U propto frac{Q_1 Q_2}{r_0} ) to compare the relative lattice energies.
- Consider Crystal Structure: If compounds have different crystal structures, consider the Madelung constant, which reflects the arrangement of ions.
4.2 Using Ionic Charge And Size To Predict Relative Lattice Energies
- Higher Ionic Charges: Compounds with higher ionic charges will generally have higher lattice energies. For example, MgO (Mg(^{2+}) and O(^{2-})) will have a higher lattice energy than NaCl (Na(^+) and Cl(^-)).
- Smaller Ionic Sizes: Compounds with smaller ions will have higher lattice energies. For example, LiF will have a higher lattice energy than CsI.
- Combined Effect: If both charge and size vary, assess their combined effect using the relationship ( U propto frac{Q_1 Q_2}{r_0} ).
4.3 Examples Of Comparing Lattice Energies
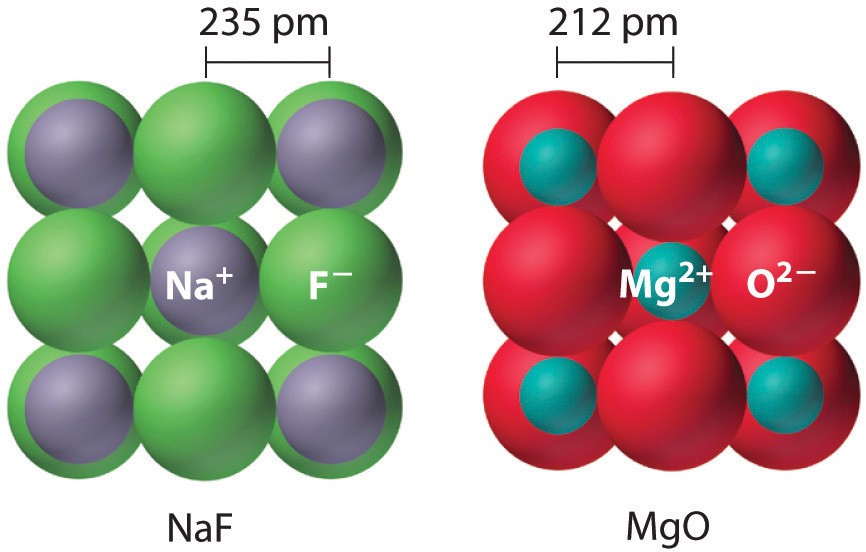
Example 1: Comparing NaCl and MgO
- NaCl: Na(^+) (charge +1), Cl(^-) (charge -1), ( r_0 ) ≈ 283 pm
- MgO: Mg(^{2+}) (charge +2), O(^{2-}) (charge -2), ( r_0 ) ≈ 212 pm
MgO has higher charges and a smaller interionic distance, so it has a significantly higher lattice energy.
Example 2: Comparing LiF and KCl
- LiF: Li(^+) (charge +1), F(^-) (charge -1), ( r_0 ) ≈ 201 pm
- KCl: K(^+) (charge +1), Cl(^-) (charge -1), ( r_0 ) ≈ 314 pm
LiF has a much smaller interionic distance, so it has a higher lattice energy.
4.4 Common Mistakes To Avoid
- Ignoring Charge: Overlooking the importance of ionic charge compared to ionic size. Charge has a more significant impact on lattice energy.
- Using Atomic Radii Instead of Ionic Radii: Using atomic radii instead of ionic radii, which can lead to incorrect interionic distances.
- Neglecting Crystal Structure: Failing to consider the crystal structure, especially when comparing compounds with different arrangements of ions.
- Not Considering Born Exponent: Neglecting the Born exponent when using Born-Mayer equation, which accounts for repulsive forces.
By avoiding these mistakes and systematically assessing ionic charges and sizes, you can accurately compare lattice energies of different ionic compounds.
5. How Does Lattice Energy Relate To Physical Properties?
Lattice energy significantly relates to physical properties such as melting point, hardness, and solubility. Higher lattice energy generally leads to higher melting points and hardness, while affecting solubility differently depending on the balance between lattice energy and hydration energy.
5.1 The Relationship Between Lattice Energy And Melting Point
Ionic compounds with high lattice energies tend to have high melting points because more energy is required to overcome the strong electrostatic attractions between ions. For example, MgO, with a high lattice energy, has a much higher melting point than NaCl, which has a lower lattice energy.
5.2 How Does Lattice Energy Affect Hardness?
Hardness, the resistance of a material to scratching or indentation, is also related to lattice energy. Compounds with higher lattice energies are generally harder because stronger ionic bonds resist deformation. Diamond, although not an ionic compound, illustrates this principle with its exceptionally strong covalent bonds leading to extreme hardness.
5.3 Lattice Energy And Solubility: What’s The Connection?
Solubility is influenced by the balance between lattice energy and hydration energy.
- Lattice Energy: Energy required to separate the ionic compound into gaseous ions.
- Hydration Energy: Energy released when gaseous ions are hydrated (surrounded by water molecules).
If hydration energy is greater than lattice energy, the compound is soluble. If lattice energy is greater, the compound is insoluble.
For example, NaCl is soluble in water because its hydration energy is slightly greater than its lattice energy. In contrast, compounds like CaCO3 are largely insoluble because their lattice energy is much greater than their hydration energy.
5.4 Examples Illustrating These Relationships
- High Melting Point: MgO (high lattice energy) has a melting point of 2852 °C, while NaCl (lower lattice energy) has a melting point of 801 °C.
- Hardness: Diamond, with strong covalent bonds, is one of the hardest known materials.
- Solubility: NaCl is soluble in water, while CaCO3 is not, reflecting the balance between hydration energy and lattice energy.
6. Comparing Lattice Energies: Case Studies
Analyzing specific ionic compounds provides practical insights into comparing lattice energies. Case studies of alkali halides and alkaline earth oxides illustrate the influence of ionic charge and size on lattice energy.
6.1 Case Study: Alkali Halides (LiF, NaCl, KBr, CsI)
Alkali halides are excellent examples to study because they have simple ionic structures and varying ionic sizes. Here’s a comparison:
| Compound | Cation | Anion | ( r_0 ) (pm) | Lattice Energy (kJ/mol) |
|---|---|---|---|---|
| LiF | Li(^+) | F(^-) | 201 | 1037 |
| NaCl | Na(^+) | Cl(^-) | 283 | 787 |
| KBr | K(^+) | Br(^-) | 329 | 682 |
| CsI | Cs(^+) | I(^-) | 395 | 600 |
As the ionic sizes increase from LiF to CsI, the lattice energy decreases, demonstrating the inverse relationship between ionic size and lattice energy.
6.2 Case Study: Alkaline Earth Oxides (MgO, CaO, SrO, BaO)
Alkaline earth oxides provide insights into the effects of both charge and size on lattice energy. All compounds have (^{2+}) cations and (^{2-}) anions, allowing us to focus on size:
| Compound | Cation | Anion | ( r_0 ) (pm) | Lattice Energy (kJ/mol) |
|---|---|---|---|---|
| MgO | Mg(^{2+}) | O(^{2-}) | 212 | 3795 |
| CaO | Ca(^{2+}) | O(^{2-}) | 240 | 3414 |
| SrO | Sr(^{2+}) | O(^{2-}) | 257 | 3220 |
| BaO | Ba(^{2+}) | O(^{2-}) | 276 | 3029 |
As the ionic sizes increase from MgO to BaO, the lattice energy decreases, again illustrating the inverse relationship between ionic size and lattice energy.
6.3 Analysis Of Trends And Exceptions
- General Trends: Lattice energy decreases with increasing ionic size and increases with increasing ionic charge.
- Exceptions: Deviations from expected trends can occur due to factors such as polarization effects and differences in crystal structure. For example, AgI has a lower lattice energy than expected due to the polarizability of the iodide ion.
6.4 Factors Contributing To Deviations From Expected Trends
- Polarization Effects: Highly charged ions can distort the electron cloud of nearby ions, affecting the electrostatic interactions and lattice energy.
- Crystal Structure Differences: Different crystal structures have different Madelung constants, which can influence the overall lattice energy.
- Covalency: Some ionic compounds have partial covalent character, which can affect their lattice energy.
7. Advanced Concepts In Lattice Energy
Advanced concepts in lattice energy include the effects of polarization, covalency, and crystal defects. Understanding these concepts provides a more nuanced view of the factors influencing lattice energy and the properties of ionic compounds.
7.1 How Does Polarization Affect Lattice Energy?
Polarization refers to the distortion of the electron cloud of an ion by the electric field of a neighboring ion. Highly charged or large ions are more polarizable, which can affect lattice energy.
- Cation Polarization: Small, highly charged cations can polarize anions, leading to a decrease in lattice energy.
- Anion Polarization: Large, highly charged anions can be polarized by cations, also leading to a decrease in lattice energy.
7.2 The Role Of Covalency In Ionic Compounds
While ionic compounds are primarily held together by electrostatic forces, some exhibit partial covalent character. This occurs when there is significant sharing of electrons between ions. Covalency can increase lattice energy by adding a covalent bonding component to the overall interaction.
7.3 Influence Of Crystal Defects On Lattice Energy
Crystal defects, such as vacancies, interstitials, and dislocations, can affect lattice energy. These defects disrupt the perfect arrangement of ions, leading to a decrease in lattice energy.
- Vacancies: Missing ions in the lattice.
- Interstitials: Extra ions located in interstitial sites.
- Dislocations: Linear defects in the crystal structure.
7.4 Computational Methods For Advanced Calculations
Computational methods, such as density functional theory (DFT) and molecular dynamics simulations, are used to calculate lattice energies and study the effects of polarization, covalency, and crystal defects. These methods provide more accurate and detailed insights into the factors influencing lattice energy.
8. Practical Applications Of Lattice Energy
Lattice energy finds practical applications in various fields, including materials science, pharmaceuticals, and environmental science. Understanding lattice energy helps in designing new materials, improving drug formulations, and developing strategies for environmental remediation.
8.1 How Is Lattice Energy Used In Materials Science?
In materials science, lattice energy is crucial for:
- Designing New Materials: By controlling the ionic interactions, materials with specific properties such as high melting points, hardness, and thermal stability can be designed.
- Predicting Material Stability: Lattice energy helps predict the stability of materials under different conditions.
- Optimizing Ceramic Manufacturing: Understanding lattice energy is essential for optimizing the sintering process in ceramics manufacturing.
8.2 Applications In The Pharmaceutical Industry
In the pharmaceutical industry, lattice energy is important for:
- Drug Formulation: Lattice energy affects the solubility, dissolution rate, and bioavailability of drugs.
- Polymorphism: Different polymorphs of a drug can have different lattice energies, affecting their physical and chemical properties.
- Drug Stability: Lattice energy helps predict the stability of drug formulations during storage.
8.3 Environmental Science: Remediation Strategies
In environmental science, lattice energy is used in:
- Predicting Mineral Solubility: Understanding the solubility of minerals helps in predicting the fate and transport of pollutants in the environment.
- Designing Remediation Strategies: Lattice energy considerations are important for designing effective remediation strategies for contaminated sites.
- Waste Management: Lattice energy helps in understanding the stability of waste materials and designing appropriate disposal methods.
8.4 Energy Storage: Batteries And Fuel Cells
Lattice energy plays a crucial role in the development of energy storage devices such as batteries and fuel cells:
- Electrolyte Design: Lattice energy affects the ionic conductivity and stability of electrolytes in batteries and fuel cells.
- Electrode Materials: Understanding lattice energy helps in designing electrode materials with high energy density and long cycle life.
- Solid-State Electrolytes: Lattice energy is particularly important in the development of solid-state electrolytes for next-generation batteries.
9. Current Research And Future Directions
Current research on lattice energy focuses on advanced computational methods, novel materials, and energy storage applications. Future directions include developing more accurate models, exploring new materials with tailored properties, and improving the performance of energy storage devices.
9.1 Advances In Computational Methods
Advances in computational methods, such as machine learning and artificial intelligence, are being used to develop more accurate models for calculating lattice energy and predicting the properties of ionic compounds. These methods can take into account complex interactions and provide detailed insights into the factors influencing lattice energy.
9.2 Exploring Novel Materials With Tailored Properties
Researchers are exploring novel materials with tailored properties by controlling the ionic interactions and crystal structures. This includes designing materials with high melting points, hardness, thermal stability, and specific optical or electronic properties.
9.3 Lattice Energy In Sustainable Energy Solutions
Lattice energy is playing an increasingly important role in sustainable energy solutions, such as:
- Solar Cells: Understanding lattice energy helps in designing stable and efficient materials for solar cells.
- Hydrogen Storage: Lattice energy considerations are important for developing materials for hydrogen storage.
- Thermoelectric Materials: Lattice energy affects the thermoelectric properties of materials, which can be used for energy generation.
9.4 Future Trends And Innovations
Future trends and innovations in lattice energy research include:
- Developing More Accurate Models: Improving the accuracy of computational models for calculating lattice energy.
- Exploring New Materials: Discovering new materials with tailored properties for specific applications.
- Integrating Computational and Experimental Methods: Combining computational and experimental methods for a more comprehensive understanding of lattice energy.
- Applying Lattice Energy in Advanced Technologies: Using lattice energy in the development of advanced technologies such as quantum computing and nanotechnology.
Lattice energy is a fundamental concept in chemistry with broad applications. COMPARE.EDU.VN can guide you in understanding and comparing lattice energies, providing the knowledge you need to excel in your scientific endeavors.
10. FAQ: Understanding Lattice Energy
10.1 What is the relationship between lattice energy and ionic bond strength?
Lattice energy is a direct measure of the strength of the ionic bonds within a compound. Higher lattice energy indicates stronger ionic bonds and greater stability.
10.2 How does ionic charge affect lattice energy?
Higher ionic charges lead to stronger electrostatic attractions between ions, resulting in greater lattice energy.
10.3 Why does ionic size matter when comparing lattice energies?
Smaller ionic sizes result in shorter interionic distances, leading to stronger attractions and higher lattice energy.
10.4 Can lattice energy be negative?
No, lattice energy is always positive. It represents the energy required to separate an ionic solid into gaseous ions, an endothermic process.
10.5 How is the Born-Haber cycle used to determine lattice energy?
The Born-Haber cycle applies Hess’s Law to relate lattice energy to other energetic terms in the formation of an ionic compound, providing an indirect experimental method to determine lattice energies.
10.6 What is the Born-Mayer equation and how is it used?
The Born-Mayer equation is used to theoretically calculate lattice energy based on crystal structure and ionic properties, accounting for both attractive and repulsive forces between ions.
10.7 How does lattice energy affect the melting point of an ionic compound?
Ionic compounds with high lattice energies tend to have high melting points because more energy is required to overcome the strong electrostatic attractions between ions.
10.8 Does lattice energy influence the solubility of ionic compounds?
Yes, solubility is influenced by the balance between lattice energy and hydration energy. If hydration energy is greater than lattice energy, the compound is soluble; otherwise, it is insoluble.
10.9 What are some practical applications of lattice energy?
Lattice energy finds practical applications in materials science, pharmaceuticals, environmental science, and energy storage.
10.10 Where can I find more information and comparisons of lattice energies?
For more in-depth information and comparisons, visit COMPARE.EDU.VN, your trusted source for detailed scientific comparisons.
Ready to dive deeper into the world of ionic compounds and lattice energy? Head over to COMPARE.EDU.VN now to explore detailed comparisons, expert analyses, and practical examples that will help you master this essential concept. Whether you’re a student, researcher, or industry professional, COMPARE.EDU.VN is your go-to resource for making informed decisions.
Don’t just compare, understand!
Visit COMPARE.EDU.VN today and unlock the power of informed decision-making. Your journey to clarity starts here.
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
WhatsApp: +1 (626) 555-9090
Website: compare.edu.vn