Lattice energy comparison can be tricky, but with the right approach, it becomes manageable. At COMPARE.EDU.VN, we simplify this process by providing comprehensive comparisons of lattice energies and the factors that influence them, empowering you to make informed decisions. Explore the elements influencing lattice energy, methods for calculating it, and how it affects ionic compound properties. Discover how to compare and predict lattice energies effectively using COMPARE.EDU.VN.
1. What Is Lattice Energy and Why Is It Important?
Lattice energy is the energy required to separate one mole of an ionic compound into its gaseous ions. It’s a measure of the strength of the ionic bonds in a crystal lattice. High lattice energy indicates strong ionic bonds, leading to greater stability and higher melting and boiling points.
Lattice energy is the measurement for the stability of ionic compounds. Understanding lattice energy is very important because:
- Predicting Compound Stability: Higher lattice energy often means a more stable compound.
- Understanding Physical Properties: Lattice energy influences melting point, boiling point, and solubility.
- Designing New Materials: Manipulating lattice energy helps in creating materials with desired properties.
2. What Factors Influence Lattice Energy?
Several factors determine the magnitude of lattice energy. Here’s a breakdown:
2.1. Ionic Charge
Ionic charge is the most significant factor. Higher charges lead to stronger electrostatic attractions, thus increasing lattice energy.
- Direct Relationship: As the charge of the ions increases, the lattice energy increases proportionally.
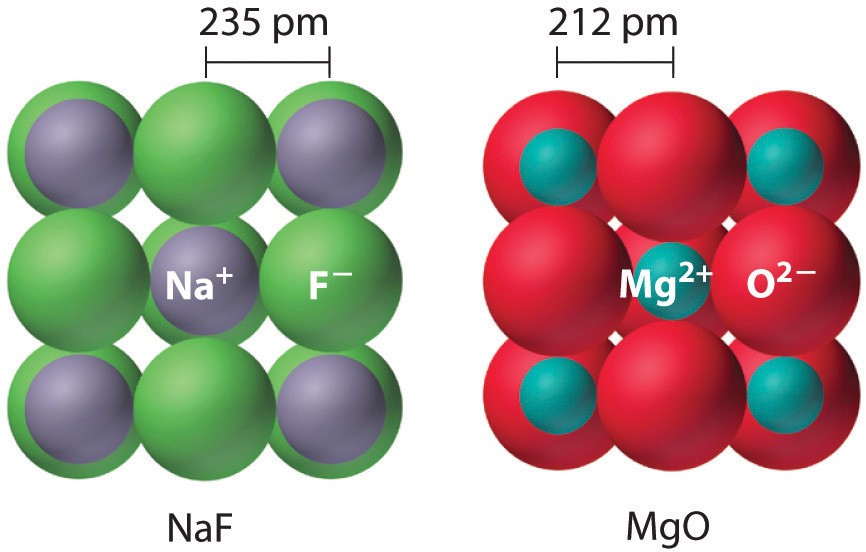
- Example: MgO (Mg²⁺ and O²⁻) has a significantly higher lattice energy than NaCl (Na⁺ and Cl⁻) due to the double charge.
2.2. Ionic Size
Ionic size is inversely related to lattice energy. Smaller ions result in shorter interionic distances and stronger attractions.
- Inverse Relationship: As the size of the ions increases, the lattice energy decreases.
- Example: LiF has a higher lattice energy than KI because Li⁺ and F⁻ are smaller than K⁺ and I⁻.
2.3. Crystal Structure
The arrangement of ions in the crystal lattice also plays a role. Different crystal structures have different coordination numbers and geometric arrangements, affecting the overall electrostatic interactions.
- Coordination Number: Higher coordination numbers generally lead to higher lattice energies.
- Structure-Specific Constants: The Madelung constant, specific to each crystal structure, accounts for these geometric effects in lattice energy calculations.
3. How to Compare Lattice Energy of Different Compounds?
When comparing the lattice energies of different compounds, consider the following steps:
3.1. Assess Ionic Charges
First, compare the charges of the ions involved. Compounds with higher charges generally have higher lattice energies.
-
Example: Comparing NaCl and CaO:
- NaCl: Na⁺, Cl⁻ (charges of +1 and -1)
- CaO: Ca²⁺, O²⁻ (charges of +2 and -2)
- CaO will have a higher lattice energy due to the greater charges.
3.2. Evaluate Ionic Sizes
If charges are the same, compare the sizes of the ions. Smaller ions lead to greater lattice energies.
-
Example: Comparing NaCl and KCl:
- NaCl: Na⁺ is smaller than K⁺.
- KCl: K⁺ is larger than Na⁺.
- NaCl will have a higher lattice energy because Na⁺ is smaller.
3.3. Consider Crystal Structures
While less common in simple comparisons, consider the crystal structure if the compounds have significantly different arrangements.
- Example: Comparing two compounds with the same ions but different structures might require more complex calculations.
3.4. Use Born-Landé Equation
For a more quantitative comparison, use the Born-Landé equation:
U = - (Nₐ * M * z⁺ * z⁻ * e²) / (4 * π * ε₀ * r₀) * (1 - 1/n)Where:
- U = Lattice energy
- Nₐ = Avogadro’s number
- M = Madelung constant
- z⁺ and z⁻ = Charges of the ions
- e = Elementary charge
- ε₀ = Vacuum permittivity
- r₀ = Shortest distance between ions
- n = Born exponent
3.5. Simplified Comparison Table
| Compound | Ionic Charges | Ionic Sizes | Lattice Energy Trend |
|---|---|---|---|
| NaCl | +1, -1 | Na⁺, Cl⁻ | Baseline |
| MgO | +2, -2 | Mg²⁺, O²⁻ | Higher due to charge |
| LiF | +1, -1 | Li⁺, F⁻ | Higher due to smaller size |
| KI | +1, -1 | K⁺, I⁻ | Lower due to larger size |
| Al₂O₃ | +3, -2 | Al³⁺, O²⁻ | Significantly higher due to high charges |

4. How Is Lattice Energy Calculated?
4.1. Born-Haber Cycle
The Born-Haber cycle is a thermodynamic cycle used to calculate lattice energy by relating it to other measurable quantities such as ionization energy, electron affinity, sublimation energy, and bond dissociation energy.
-
Steps in Born-Haber Cycle:
- Sublimation (ΔHsub): Solid metal to gaseous atoms.
- Ionization Energy (IE): Gaseous atoms to gaseous ions (for the cation).
- Dissociation Energy (ΔHdiss): Diatomic gas to individual gaseous atoms (for the anion).
- Electron Affinity (EA): Gaseous atoms to gaseous ions (for the anion).
- Formation (ΔHform): Elements in their standard states to the ionic compound.
-
Equation:
ΔHform = ΔHsub + IE + 1/2 * ΔHdiss + EA + U
Rearranging for lattice energy (U):
U = ΔHform – (ΔHsub + IE + 1/2 * ΔHdiss + EA)
4.2. Born-Landé Equation
As mentioned earlier, the Born-Landé equation provides a theoretical estimate of lattice energy based on ionic charges, sizes, and crystal structure.
-
Equation:
U = – (Nₐ M z⁺ z⁻ e²) / (4 π ε₀ r₀) (1 – 1/n)
-
Variables and Their Impact:
- Madelung Constant (M): Depends on the crystal structure.
- Born Exponent (n): Related to the hardness of the ions.
4.3. Kapustinskii Equation
The Kapustinskii equation is a simplified version of the Born-Landé equation, which is useful when the crystal structure is unknown.
-
Equation:
U ≈ (1.202 × 10⁻¹⁰ J⋅m/mol) (|z⁺| |z⁻| * Nₐ) / (r⁺ + r⁻)
Where:
- z⁺ and z⁻ are the charges of the ions
- Nₐ is Avogadro’s number
- r⁺ and r⁻ are the radii of the ions
Note: The Kapustinskii equation provides an approximate value but is handy when detailed structural data is unavailable.
5. What are the Trends in Lattice Energy?
Understanding the trends in lattice energy helps in predicting the properties of ionic compounds.
5.1. Periodic Trends
- Across a Period: Lattice energy generally increases as you move from left to right across the periodic table due to increasing ionic charges (e.g., NaF < MgO < Al₂O₃).
- Down a Group: Lattice energy generally decreases as you move down a group due to increasing ionic sizes (e.g., LiF > NaF > KF > RbF > CsF).
5.2. Compound Comparisons
- Same Anion, Different Cation: For compounds with the same anion, lattice energy decreases as the size of the cation increases (e.g., LiCl > NaCl > KCl).
- Same Cation, Different Anion: For compounds with the same cation, lattice energy decreases as the size of the anion increases (e.g., NaF > NaCl > NaBr > NaI).
5.3. Charge Dominance
The effect of ionic charge is usually more significant than ionic size. For example, MgO (with +2 and -2 charges) will have a higher lattice energy than NaCl (with +1 and -1 charges), even though the ions in MgO might be slightly larger.
6. Lattice Energy and Physical Properties
Lattice energy significantly influences several physical properties of ionic compounds.
6.1. Melting and Boiling Points
Higher lattice energy typically results in higher melting and boiling points because more energy is required to overcome the strong electrostatic forces holding the ions together.
- Example: MgO, with its high lattice energy, has a much higher melting point than NaCl.
6.2. Solubility
Lattice energy affects solubility. For a compound to dissolve, the energy released during solvation (hydration) must be greater than the lattice energy.
- High Lattice Energy: Compounds with very high lattice energies are often insoluble because the solvation energy cannot compensate for the energy required to break the lattice.
- Factors Affecting Solubility: Other factors such as ion-dipole interactions and entropy also play a role.
6.3. Hardness and Brittleness
Ionic compounds are generally hard but brittle. The strong electrostatic forces make them hard, but when subjected to stress, the ions can shift, leading to repulsion and fracture.
- Lattice Energy Impact: Higher lattice energy contributes to increased hardness.
7. Practical Examples of Lattice Energy Comparisons
7.1. Comparing Alkali Halides
Consider the alkali halides (LiF, NaCl, KBr, etc.). Lattice energy decreases down the group due to increasing ionic sizes.
-
Example:
- LiF: High lattice energy due to small Li⁺ and F⁻ ions.
- NaCl: Moderate lattice energy.
- KBr: Lower lattice energy due to larger K⁺ and Br⁻ ions.
7.2. Comparing Oxides and Halides
Comparing oxides (like MgO) and halides (like NaCl) illustrates the impact of ionic charge.
-
Example:
- MgO: High lattice energy due to +2 and -2 charges.
- NaCl: Lower lattice energy due to +1 and -1 charges.
7.3. Ordering Compounds by Lattice Energy
Given a set of compounds, you can predict their relative lattice energies based on the principles discussed.
-
Example: Arrange the following in order of increasing lattice energy: NaCl, MgO, LiF, KBr.
- KBr (lowest, larger ions, +1/-1 charge)
- NaCl (moderate, smaller ions than KBr, +1/-1 charge)
- LiF (high, small ions, +1/-1 charge)
- MgO (highest, +2/-2 charge)
8. Advanced Concepts in Lattice Energy
8.1. Polarization Effects
Ions are not perfectly rigid spheres, and they can be polarized, which means their electron clouds can be distorted by nearby ions. This effect is more pronounced with highly charged and small ions.
- Polarization Energy: Polarization can increase the effective attraction between ions, leading to a higher lattice energy than predicted by simple models.
- Fajan’s Rules: These rules help predict when polarization effects are significant. Small, highly charged cations and large, highly charged anions are more polarizing.
8.2. Covalency
In some ionic compounds, the bonding is not purely ionic but has some covalent character. This is particularly true when there is a significant difference in electronegativity between the ions.
- Partial Covalent Character: Covalent character can increase the lattice energy by adding a directional component to the bonding.
- Example: Silver halides (AgCl, AgBr, AgI) have higher lattice energies than expected due to covalent contributions.
8.3. Defects in Crystal Lattices
Real crystals are not perfect; they contain defects such as vacancies (missing ions) and interstitials (extra ions). These defects can affect the lattice energy.
- Vacancy Formation: Creating vacancies requires energy, effectively reducing the overall lattice energy.
- Types of Defects: Schottky defects (equal numbers of cation and anion vacancies) and Frenkel defects (ion displaced to an interstitial site) have different effects on lattice energy.
9. Computational Methods for Lattice Energy
9.1. Density Functional Theory (DFT)
DFT is a quantum mechanical method used to calculate the electronic structure of materials, including ionic compounds. It can provide accurate estimates of lattice energy by considering the interactions between all electrons and nuclei in the crystal.
- Advantages: Accurate for many systems, can handle complex crystal structures.
- Limitations: Computationally intensive, requires significant computational resources.
9.2. Molecular Dynamics (MD) Simulations
MD simulations involve simulating the motion of atoms and ions in a crystal over time. By calculating the potential energy of the system, lattice energy can be estimated.
- Advantages: Can simulate dynamic processes, allows for temperature effects to be included.
- Limitations: Requires accurate interatomic potentials, can be computationally expensive for large systems.
9.3. Hybrid Methods
Combining DFT and MD can provide a balance between accuracy and computational cost. For example, DFT can be used to calculate the electronic structure, while MD is used to simulate the dynamics.
10. Applications of Lattice Energy
10.1. Materials Science
Understanding lattice energy is crucial in materials science for designing and synthesizing new materials with desired properties.
- High-Temperature Superconductors: Lattice energy plays a role in the stability and performance of these materials.
- Battery Materials: Lattice energy affects the ionic conductivity and stability of electrode materials in batteries.
10.2. Geochemistry
Lattice energy influences the formation and stability of minerals in the Earth’s crust and mantle.
- Mineral Stability: Minerals with high lattice energies are more stable under extreme conditions.
- Geochemical Processes: Lattice energy affects the solubility and mobility of ions in geological fluids.
10.3. Pharmaceutical Science
Lattice energy is important in pharmaceutical science for understanding the stability and solubility of drug compounds.
- Drug Formulation: The lattice energy of a drug affects its dissolution rate and bioavailability.
- Salt Selection: Choosing the right salt form of a drug can optimize its lattice energy and improve its properties.
11. Common Mistakes to Avoid When Comparing Lattice Energy
11.1. Ignoring Ionic Charges
A common mistake is to focus solely on ionic sizes and neglect the impact of ionic charges. Remember that charge has a more significant effect on lattice energy.
- Correct Approach: Always consider the charges of the ions first before comparing their sizes.
11.2. Overlooking Crystal Structure
In most basic comparisons, crystal structure can be overlooked. However, for compounds with different structures and similar charges and sizes, consider the Madelung constant.
- Correct Approach: Be aware of the crystal structure if the other factors are too close to call.
11.3. Not Considering Polarization Effects
For compounds with highly charged and small ions, polarization effects can be significant. Neglecting this can lead to inaccurate predictions.
- Correct Approach: Consider polarization effects, especially when dealing with small, highly charged ions.
12. Real-World Applications of Understanding Lattice Energy
12.1. Designing Better Batteries
In the development of lithium-ion batteries, understanding lattice energy helps in selecting electrode materials that allow for faster ion transport and greater stability.
- Lithium Iron Phosphate (LiFePO₄): This material has a stable lattice structure, which contributes to its long cycle life and safety in batteries.
12.2. Creating Stronger Ceramics
Ceramic materials with high lattice energies are often harder and more resistant to wear. This makes them suitable for applications in cutting tools, abrasives, and protective coatings.
- Aluminum Oxide (Al₂O₃): Known for its high lattice energy, making it an excellent abrasive and cutting tool material.
12.3. Improving Drug Delivery
In the pharmaceutical industry, lattice energy is considered when formulating drugs to control their solubility and release rate in the body.
- Salt Forms of Drugs: By choosing the appropriate salt form, the lattice energy can be optimized to improve drug delivery and efficacy.
13. Future Trends in Lattice Energy Research
13.1. Advanced Computational Techniques
Future research will likely focus on developing more advanced computational techniques to accurately predict lattice energies for complex systems.
- Machine Learning: Machine learning algorithms can be trained on existing data to predict lattice energies for new compounds.
13.2. Exploring New Materials
Lattice energy will play a crucial role in the discovery and development of new materials for various applications, including energy storage, catalysis, and electronics.
- Perovskites: These materials are being explored for their potential in solar cells and other applications, and understanding their lattice energies is essential for optimizing their performance.
13.3. Understanding Defect Chemistry
Future studies will focus on understanding how defects in crystal lattices affect lattice energy and material properties.
- Defect Engineering: Manipulating the concentration and type of defects in a crystal can tailor its properties for specific applications.
14. FAQ: Frequently Asked Questions About Lattice Energy
14.1. What is the difference between lattice energy and bond energy?
Lattice energy refers to the energy required to separate an ionic compound into gaseous ions, while bond energy refers to the energy required to break a covalent bond.
14.2. How does lattice energy affect the solubility of ionic compounds?
Higher lattice energy generally decreases solubility because more energy is required to break the lattice, while solvation energy needs to be greater than lattice energy for dissolution.
14.3. Can lattice energy be negative?
No, lattice energy is always defined as a positive value, representing the energy required to break the ionic lattice. The energy released during the formation of the lattice is negative.
14.4. Why is the Born-Haber cycle important?
The Born-Haber cycle is important because it relates lattice energy to other measurable thermodynamic quantities, allowing for its calculation.
14.5. How do ionic size and charge affect lattice energy?
Lattice energy is directly proportional to ionic charge and inversely proportional to ionic size. Higher charges and smaller sizes lead to higher lattice energies.
14.6. What is the Kapustinskii equation used for?
The Kapustinskii equation is used to estimate lattice energy when the crystal structure is unknown, providing an approximate value based on ionic charges and radii.
14.7. What are some real-world applications of lattice energy?
Real-world applications include designing better batteries, creating stronger ceramics, and improving drug delivery.
14.8. How does polarization affect lattice energy?
Polarization can increase the effective attraction between ions, leading to a higher lattice energy than predicted by simple models.
14.9. What is the Madelung constant?
The Madelung constant is a structure-specific constant that accounts for the geometric arrangement of ions in a crystal lattice, affecting the overall electrostatic interactions.
14.10. Why is understanding lattice energy important for materials science?
Understanding lattice energy is crucial in materials science for designing and synthesizing new materials with desired properties, such as high-temperature superconductors and battery materials.
15. Conclusion: Mastering Lattice Energy Comparisons
Understanding How To Compare Lattice Energy involves assessing ionic charges, sizes, and crystal structures. Use equations like the Born-Landé and Kapustinskii equations for quantitative comparisons. Lattice energy influences melting points, solubility, hardness, and various applications in materials science, geochemistry, and pharmaceutical science. For detailed comparisons and reliable information, visit COMPARE.EDU.VN, your trusted resource for informed decision-making.
Navigating the complexities of lattice energy doesn’t have to be challenging. At COMPARE.EDU.VN, we provide the tools and information you need to compare and understand lattice energies effectively. Whether you’re a student, researcher, or industry professional, our resources can help you make informed decisions and gain a deeper understanding of ionic compounds.
Ready to explore more comparisons and make informed decisions? Visit compare.edu.vn today. Contact us at 333 Comparison Plaza, Choice City, CA 90210, United States or reach out via Whatsapp at +1 (626) 555-9090.
