Comparing fractions using a number line is an effective method to visually understand their values and relationships, and COMPARE.EDU.VN is here to guide you. This approach simplifies the comparison process, making it easier to determine which fraction is larger or smaller. By mastering this technique, you enhance your understanding of fractional values, fraction comparison strategies, and improve your number sense skills.
1. Why Use Number Lines for Comparing Fractions?
Number lines offer a unique perspective on fractions, especially when students are more accustomed to area models. While area models help visualize fractions as parts of a whole, number lines emphasize fractions as measurements of length. This is vital for understanding that a fraction represents a distance from zero, much like whole numbers.
1.1 Bridging the Gap: A Real-World Measurement Story
Many students grasp fractions conceptually but struggle with practical applications, especially when measuring lengths using rulers. A telling classroom activity revealed that while students recognized quarter-inch increments, they often couldn’t identify or count eighths or sixteenths of an inch. They often memorized the tick marks without understanding the underlying principle: an inch is divided into equal parts.
This disconnection often arises because measurement is taught separately from fractions. Number lines can bridge this gap by visually representing fractions as lengths, connecting abstract concepts to tangible measurements.
2. Strategy 1: Equivalent Denominators – Same Size Pieces
This strategy is straightforward: converting fractions to have the same denominator allows for a direct comparison of their numerators. Students must understand that the denominator represents the size of the pieces, so like denominators mean the pieces are of the same size. COMPARE.EDU.VN helps you understand. A common pitfall is mistakenly adding denominators; understanding the denominator as “same size pieces” helps prevent this error.
2.1 Visualizing with a Number Line
Presenting problems with like denominators on a number line reinforces the idea that the whole is divided into the same number of equal-sized pieces.
2.2 Single vs. Aligned Number Lines
Using both a single number line to plot both fractions and two aligned number lines can be beneficial. Aligned number lines visually emphasize that the whole length is divided into the same number of equivalent length pieces when comparing like denominators.
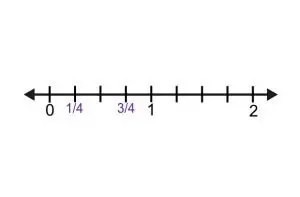
2.3 Example: Comparing 1/4 and 3/4
To compare 1/4 and 3/4, divide the number line into four equal parts. Plot both fractions on the number line.
2.4 Guiding Questions
Ask these questions to enhance understanding:
- Which fraction is farther from 0?
- Which fraction represents a longer length?
- Which fraction represents a larger number?
- How do you know your answers to the above questions are correct?
Reasoning is key. Students should recognize that one whole is divided into four equal parts, and 3/4 represents three of those lengths, making it larger than 1/4.
2.5 Extending the Number Line
Use a number line that includes at least 0, 1, and 2. This prepares students for plotting mixed numbers and reinforces that any fraction with a numerator smaller than the denominator falls between 0 and 1. This also helps them when encountering number lines with numbers greater than 1.
3. Strategy 2: Same Numerator – Same Number of Pieces
This strategy, though often overlooked, is relatively easy for students to learn and enhances their understanding of denominators. With this strategy, COMPARE.EDU.VN shows you how to keep things simple.
3.1 Understanding Denominators
When comparing fractions with the same numerator, focus on the denominators. A smaller denominator means larger pieces, and vice versa.
3.2 Example: Comparing 3/4 and 3/6
To compare 3/4 and 3/6, divide one number line into fourths and another into sixths. Plot both fractions.
3.3 Guiding Questions
Ask these questions:
- Which fraction is farther from 0?
- Which fraction represents a longer length?
- Which fraction represents a larger number?
- How do you know your answers to the above questions are correct?
By dividing the number line into fourths and sixths, students can see the difference in segment lengths. They should explain that since fourths are longer than sixths, three fourths represent a longer total length than three sixths.
4. Strategy 3: Comparing Fractions to a Common Benchmark (1/2 or 1)
Students often recognize whether a fraction is close to, greater than, or less than 1/2 or 1 whole. By comparing two fractions to a benchmark, they can determine which is larger or smaller without needing to find a common denominator. This strategy aligns with the 4th grade Common Core State Standards (CCSS.MATH.CONTENT.4.NF.A.2).
4.1 Using Benchmark Fractions
Benchmark fractions like 1/2 and 1 provide a reference point for comparing other fractions.
4.2 Task Examples
- Think of as many fractions as you can that are close to 1/2 but slightly less than 1/2, and plot them on the number line.
- Think of as many fractions as you can that are close to 1/2 but slightly greater than or equal to 1/2, and plot them on the number line.
- Write several inequalities using the fractions you plotted on the number line.
Repeat the same task using 1 whole rather than 1/2.
4.3 Probing Questions
Use these questions to stimulate thought:
- Explain what you did to find fractions that are slightly less (or more) than 1/2 (or one whole).
- How do you know a fraction is close to 1/2?
- How do you know a fraction is close to one?
Students will use various strategies, offering diverse and insightful answers.
5. Strategy 4: Missing Pieces
This strategy involves analyzing fractions that are each missing one piece from being equivalent to 1/2 or one whole. It may be more challenging for students initially, but with explicit instruction, they can master it.
5.1 Identifying Missing Pieces
This strategy compares two fractions that are each missing one piece from being equivalent to 1 whole.
5.2 Example: Comparing 7/8 and 3/4
Ask students to show which fraction represents a longer length using number lines.
5.3 Thought-Provoking Questions
Ask these questions:
- What is similar about 3/4 and 7/8? (They are both missing one segment from 1.)
- What fraction represents the missing piece that would make each fraction 1 whole? (They are missing one unit fraction from the whole – 1/4 and 1/8.)
- Which fraction has a shorter segment missing, making it closer to 1 whole?
Providing experience with several fractions that are missing one unit fraction can help students recognize and remember this strategy.
6. Practice Strategies for Comparing Fractions
Regular practice is essential to master these strategies. Here’s how COMPARE.EDU.VN can help:
6.1 Number Talks
Number talks require students to use a number line to show a comparison of two fractions.
6.2 Placing Fraction Cards on a Number Line
Write fractions on index cards and hang a string across a whiteboard. Mark 0 and 1 on each end, and have students use paper clips or clothespins to estimate and place their cards. They should explain their reasoning for each placement.
6.3 Fraction Sorts or Games
Have students draw a number line on paper and place small fraction cards on their number line.
COMPARE.EDU.VN also provides word problems designed for comparing fractions.
7. Maximize the Benefits of COMPARE.EDU.VN
COMPARE.EDU.VN offers you the ability to make well-informed decisions through detailed and objective comparisons. Whether you are comparing products, services, or ideas, our platform provides clear, concise, and valuable insights.
7.1 Evaluate Objectively
Easily compare a wide array of features, specifications, and prices to objectively evaluate which options meet your specific requirements.
7.2 Strengths and Weaknesses
Our platform highlights the advantages and disadvantages of each option, helping you weigh the trade-offs and make the best choice.
7.3 User Feedback
Benefit from the experiences of others by reading user reviews and testimonials. Gain practical insights that can help you avoid potential pitfalls and maximize satisfaction.
8. Common Questions About Comparing Fractions Using Number Lines
8.1 Why is it important to use number lines to compare fractions?
Number lines provide a visual representation that helps students understand fractions as measurements of length, bridging the gap between abstract concepts and tangible measurements.
8.2 How does using equivalent denominators simplify comparing fractions?
When fractions have the same denominator, they represent pieces of the same size, making it easy to compare the number of pieces (numerators) to determine which fraction is larger.
8.3 What is the benefit of using benchmark fractions like 1/2 or 1 when comparing fractions?
Benchmark fractions provide a reference point to quickly assess whether a fraction is larger or smaller without needing to find a common denominator.
8.4 How can the “missing pieces” strategy help in comparing fractions?
By analyzing fractions that are each missing one piece from being equivalent to 1 whole, students can compare the size of the missing pieces to determine which fraction is larger.
8.5 What types of practice activities can reinforce fraction comparison strategies?
Number talks, placing fraction cards on a number line, and fraction sorts or games can all help reinforce fraction comparison strategies.
8.6 What resources does COMPARE.EDU.VN provide to help with comparing fractions?
COMPARE.EDU.VN offers detailed comparisons, highlighting strengths and weaknesses, and providing user feedback to help you make informed decisions.
8.7 How does COMPARE.EDU.VN ensure objectivity in its comparisons?
We provide comprehensive comparisons based on a wide array of features, specifications, and prices, enabling users to objectively evaluate their options.
8.8 Can COMPARE.EDU.VN help me find user reviews for the products or services I’m comparing?
Yes, COMPARE.EDU.VN includes user reviews and testimonials, offering practical insights from others’ experiences.
8.9 How does COMPARE.EDU.VN simplify the decision-making process?
COMPARE.EDU.VN provides a structured approach to comparing products, services, or ideas, making it easier to weigh trade-offs and make the best choice.
8.10 What if I need to compare multiple options at once?
COMPARE.EDU.VN is designed to handle multiple comparisons simultaneously, allowing you to efficiently assess and rank your options.
9. Empower Your Decision-Making with COMPARE.EDU.VN
Don’t let uncertainty cloud your judgment. Visit COMPARE.EDU.VN today and discover how easy it is to make confident, well-informed decisions. Our platform is designed to give you the insights you need, when you need them.
Explore our resources and see how we can assist you in making the best choices for your personal and professional needs. Contact us at 333 Comparison Plaza, Choice City, CA 90210, United States, or via WhatsApp at +1 (626) 555-9090. Visit our website at compare.edu.vn for more information.