Comparing fractions quickly is a fundamental skill in mathematics, essential for various applications. COMPARE.EDU.VN offers a comprehensive guide on mastering this skill, covering various techniques to efficiently compare fractions, whether they have the same or different denominators. Learn how to quickly compare fractions and simplify mathematical tasks with ease, understanding equivalent fractions, and applying these skills in real-world scenarios.
1. Understanding the Basics of Fractions for Quick Comparison
Before diving into the methods for comparing fractions, it’s crucial to grasp the fundamental concepts of what fractions represent. A fraction is a part of a whole, expressed as a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, and the numerator indicates how many of those parts we’re considering. Understanding this relationship is key to comparing fractions effectively. Knowing the components of a fraction—numerator and denominator—and what they signify is foundational for comparing fractional values.
1.1. Numerator and Denominator Explained
The numerator represents the specific number of parts you have, while the denominator represents the total number of parts that make up the whole. For example, in the fraction 3/4, 3 is the numerator, indicating you have three parts, and 4 is the denominator, indicating the whole is divided into four equal parts. When comparing fractions, you’re essentially determining which fraction represents a larger portion of its whole.
1.2. Different Types of Fractions
Fractions can be categorized into several types, each requiring slightly different comparison strategies:
- Proper Fractions: The numerator is less than the denominator (e.g., 2/5).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 7/3).
- Mixed Numbers: A whole number combined with a proper fraction (e.g., 1 1/2).
- Equivalent Fractions: Fractions that represent the same value, even with different numerators and denominators (e.g., 1/2 and 2/4).
Understanding these types is critical for choosing the most efficient comparison method.
1.3. Simplifying Fractions for Easier Comparison
Simplifying fractions, also known as reducing fractions to their lowest terms, involves dividing both the numerator and the denominator by their greatest common factor (GCF). This process makes fractions easier to compare by reducing them to their simplest form. For example, the fraction 4/8 can be simplified to 1/2 by dividing both the numerator and denominator by 4. Simplified fractions make comparisons more straightforward.
2. Quick Comparison Techniques for Fractions with the Same Denominator
When fractions share the same denominator, comparing them becomes incredibly straightforward. The fraction with the larger numerator is the larger fraction. This simple rule forms the basis for quick comparisons when the denominators are uniform.
2.1. The Rule: Larger Numerator Means Larger Fraction
If two or more fractions have the same denominator, the fraction with the highest numerator represents the greatest value. This is because all fractions are dividing the whole into the same number of parts (the denominator), so the fraction with more parts (the numerator) is larger. For example, 5/8 is greater than 3/8 because 5 is greater than 3.
2.2. Examples of Comparing Fractions with the Same Denominator
Consider the following examples:
- Comparing 2/7 and 5/7: Since both fractions have a denominator of 7, we simply compare the numerators. 5 is greater than 2, so 5/7 > 2/7.
- Comparing 9/11 and 4/11: Again, both fractions share the same denominator. Comparing the numerators, 9 is greater than 4, thus 9/11 > 4/11.
These examples illustrate how quickly you can determine the larger fraction when the denominators are the same.
2.3. Practice Exercises for Mastering the Technique
Test your understanding with these practice exercises:
- Which is larger: 3/10 or 7/10?
- Which is smaller: 8/15 or 2/15?
- Compare: 11/20 and 13/20.
By practicing these types of problems, you’ll quickly master the technique of comparing fractions with the same denominator.
3. Mastering Fraction Comparison with Different Denominators: Quick Techniques
Comparing fractions with unlike denominators requires a bit more work, but several quick techniques can make the process manageable. These methods involve finding a common denominator or using cross-multiplication.
3.1. Finding a Common Denominator: The LCM Method
The most common method for comparing fractions with different denominators is to find the least common multiple (LCM) of the denominators. Once you find the LCM, convert each fraction so that it has this new denominator. Then, you can compare the numerators as you would with fractions that have the same denominator. For example, to compare 1/3 and 1/4, the LCM of 3 and 4 is 12. Convert 1/3 to 4/12 and 1/4 to 3/12. Now you can easily see that 4/12 > 3/12, so 1/3 > 1/4.
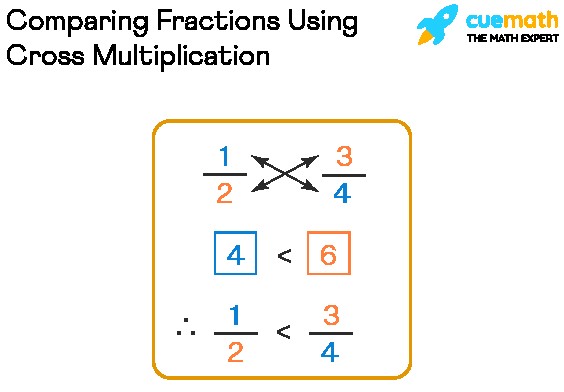
3.2. Cross-Multiplication: A Quick Comparison Trick
Cross-multiplication is a quick and efficient way to compare two fractions. Multiply the numerator of the first fraction by the denominator of the second fraction, and then multiply the numerator of the second fraction by the denominator of the first fraction. Compare the results. The fraction corresponding to the larger result is the larger fraction. For example, to compare 2/5 and 3/7, multiply 2 by 7 (result is 14) and 3 by 5 (result is 15). Since 15 is greater than 14, 3/7 > 2/5.
3.3. Real-World Examples and Practical Applications
These techniques aren’t just theoretical; they have real-world applications. For instance, if you’re baking and need to compare ingredient amounts (e.g., 2/3 cup of flour vs. 3/4 cup of sugar), you can use these methods to determine which ingredient you need more of. Similarly, in financial contexts, you might need to compare fractions of investments to determine which is performing better.
4. Visual Methods for Quick Fraction Comparison
Visual aids can make comparing fractions more intuitive and faster, especially for those who are visual learners. Using diagrams and number lines provides a clear, visual representation of the fractions’ values.
4.1. Using Fraction Bars or Pie Charts
Fraction bars and pie charts are excellent tools for visually representing fractions. Draw or use pre-made diagrams where each fraction is shown as a part of a whole. By visually comparing the shaded areas, you can quickly determine which fraction is larger. For example, if you have a fraction bar representing 1/2 and another representing 2/5, you can see at a glance that 1/2 covers more area, thus 1/2 > 2/5.
4.2. Number Lines for Quick Visual Assessments
Number lines provide a linear representation of fractions, making it easy to see their relative positions. Draw a number line and mark the fractions you want to compare. The fraction that is further to the right on the number line is the larger fraction. For example, if you plot 1/4 and 1/2 on a number line, 1/2 will be to the right of 1/4, indicating that 1/2 > 1/4.
4.3. Making Visuals Work for Quick, Intuitive Comparisons
Visual methods are particularly helpful for quick, intuitive comparisons. They eliminate the need for complex calculations and provide an immediate visual answer. These methods are especially useful for teaching children or for anyone who struggles with abstract mathematical concepts.
5. Converting Fractions to Decimals for Quick and Easy Comparison
Converting fractions to decimals is a straightforward method that allows for easy comparison, especially when dealing with multiple fractions or complex values. This approach simplifies the process by transforming fractions into a format that is readily comparable.
5.1. The Process: Dividing Numerator by Denominator
To convert a fraction to a decimal, simply divide the numerator by the denominator. For example, to convert 3/4 to a decimal, divide 3 by 4, which equals 0.75. This process transforms the fraction into a decimal value that can be easily compared with other decimal values.
5.2. Comparing Decimal Values for Quick Decisions
Once the fractions are converted to decimals, comparing them is as simple as comparing decimal values. For example, if you have 3/4 (0.75) and 4/5 (0.8), you can quickly see that 0.8 is greater than 0.75, therefore 4/5 > 3/4. This method is particularly useful when dealing with fractions that are difficult to compare using other methods.
5.3. Advantages and Limitations of Using Decimals
The advantage of using decimals is the ease of comparison. However, some fractions result in repeating decimals, which may require rounding and can introduce slight inaccuracies. Despite this limitation, converting to decimals is generally a quick and reliable method for comparing fractions.
6. Benchmark Fractions: A Quick Way to Estimate and Compare
Using benchmark fractions like 0, 1/2, and 1 as reference points can significantly speed up the comparison process. This technique involves estimating where a fraction falls in relation to these benchmarks, allowing for quicker comparisons.
6.1. Understanding and Using 0, 1/2, and 1 as Benchmarks
Benchmark fractions are easy to visualize and understand. A fraction close to 0 has a very small numerator compared to its denominator (e.g., 1/10). A fraction close to 1/2 has a numerator that is approximately half of its denominator (e.g., 5/11). A fraction close to 1 has a numerator nearly equal to its denominator (e.g., 9/10).
6.2. Estimating Fractions Relative to Benchmarks
To use benchmark fractions, estimate where a given fraction falls relative to 0, 1/2, or 1. For example, consider 3/8. Since half of 8 is 4, 3/8 is slightly less than 1/2. Now consider 5/9. Since half of 9 is 4.5, 5/9 is slightly more than 1/2. Therefore, we can quickly deduce that 5/9 > 3/8 without needing to find a common denominator or convert to decimals.
6.3. Speeding Up Comparisons with Estimation Skills
This method relies on estimation skills, which can be honed with practice. By frequently estimating fractions relative to benchmarks, you can quickly compare fractions in your head, making it a valuable skill for everyday situations.
7. Comparing Mixed Numbers and Improper Fractions Quickly
Mixed numbers and improper fractions require a preliminary step before comparison: converting them into a common format. This conversion makes the comparison process straightforward and efficient.
7.1. Converting Mixed Numbers to Improper Fractions
To convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator. Keep the same denominator. For example, to convert 2 3/4 to an improper fraction, multiply 2 by 4 (which is 8), add 3 (which gives 11), and keep the denominator 4. So, 2 3/4 = 11/4.
7.2. Comparing Improper Fractions Directly
Once mixed numbers are converted to improper fractions, you can compare them using the methods discussed earlier, such as finding a common denominator or cross-multiplication. For example, to compare 11/4 and 7/3, find the common denominator (12). Convert 11/4 to 33/12 and 7/3 to 28/12. Now you can easily see that 33/12 > 28/12, so 11/4 > 7/3.
7.3. Practical Examples and Step-by-Step Solutions
Let’s walk through an example: Compare 1 1/2 and 2 1/4.
First, convert both to improper fractions:
- 1 1/2 = 3/2
- 2 1/4 = 9/4
Next, find a common denominator (4):
- 3/2 = 6/4
Now compare:
- 6/4 < 9/4
Therefore, 1 1/2 < 2 1/4.
8. Common Mistakes to Avoid When Comparing Fractions Quickly
Even with efficient techniques, it’s easy to make mistakes when comparing fractions quickly. Awareness of these common pitfalls can help you avoid errors and ensure accurate comparisons.
8.1. Misunderstanding the Role of the Denominator
One common mistake is assuming that a larger denominator always means a larger fraction. Remember that the denominator indicates the number of parts the whole is divided into, so a larger denominator means each part is smaller. For example, 1/5 is larger than 1/10 because the whole is divided into fewer parts, making each part larger.
8.2. Incorrectly Applying Cross-Multiplication
Cross-multiplication can be tricky if not applied correctly. Always multiply the numerator of the first fraction by the denominator of the second fraction and compare the result to the product of the numerator of the second fraction and the denominator of the first fraction. Make sure you associate the correct product with the corresponding fraction.
8.3. Forgetting to Simplify Before Comparing
Failing to simplify fractions before comparing can lead to unnecessary complexity. Simplifying fractions to their lowest terms makes the comparison process much easier. For example, comparing 4/8 and 2/5 is more difficult than comparing 1/2 and 2/5.
9. Practice Exercises to Sharpen Your Quick Comparison Skills
Consistent practice is key to mastering the art of quickly comparing fractions. These exercises will help you hone your skills and build confidence.
9.1. Basic Comparison Drills
Compare the following fractions using any method you prefer:
- 2/3 and 3/4
- 1/5 and 2/10
- 5/8 and 7/12
- 3/7 and 4/9
- 11/15 and 13/20
9.2. Advanced Comparison Problems
Compare the following mixed numbers and improper fractions:
- 1 1/4 and 5/3
- 2 2/5 and 11/4
- 3 1/2 and 7/2
- 15/4 and 3 3/4
- 4 1/3 and 13/3
9.3. Real-World Application Questions
- You have 2/5 of a pizza, and your friend has 3/8 of a pizza. Who has more pizza?
- A recipe calls for 1 1/2 cups of flour and 5/4 cups of sugar. Which ingredient do you need more of?
- You ran 3/5 of a mile, and your friend ran 5/8 of a mile. Who ran farther?
10. Leveraging COMPARE.EDU.VN for Mastering Fraction Comparisons
COMPARE.EDU.VN offers a wealth of resources designed to help you master fraction comparisons. From detailed explanations to interactive tools, you’ll find everything you need to sharpen your skills.
10.1. How COMPARE.EDU.VN Simplifies Fraction Comparisons
At COMPARE.EDU.VN, we understand that comparing fractions can be challenging. That’s why we’ve created a platform with easy-to-understand guides, visual aids, and practice exercises. Our resources are designed to simplify the comparison process, making it accessible to learners of all levels.
10.2. Interactive Tools and Resources Available
Explore our interactive tools, such as fraction calculators and visual comparison tools, to enhance your learning experience. These resources provide immediate feedback and help you visualize fraction comparisons in a dynamic way.
10.3. Further Learning and Advanced Techniques
For those looking to delve deeper, COMPARE.EDU.VN offers advanced techniques and resources, including articles on complex fraction problems and strategies for quick mental calculations. Expand your knowledge and become a fraction comparison expert with our comprehensive learning materials.
Mastering the skill of comparing fractions quickly involves understanding fundamental concepts, practicing efficient techniques, and avoiding common mistakes. With the resources available at COMPARE.EDU.VN, you can confidently tackle any fraction comparison problem. Ready to enhance your skills? Visit COMPARE.EDU.VN today and discover a world of educational resources designed to make learning math easier and more effective. Our platform offers comprehensive comparisons, ensuring you always make informed decisions.
For further assistance or inquiries, please contact us at 333 Comparison Plaza, Choice City, CA 90210, United States, or reach us via Whatsapp at +1 (626) 555-9090.
FAQs About How To Compare Fractions Quickly
1. What is the quickest way to compare fractions?
The quickest way to compare fractions depends on the fractions themselves. If they have the same denominator, simply compare the numerators. If they have different denominators, cross-multiplication or converting to decimals are often the fastest methods.
2. How do you compare fractions with different denominators?
To compare fractions with different denominators, find a common denominator (usually the least common multiple), convert the fractions to have this denominator, and then compare the numerators. Alternatively, you can use cross-multiplication or convert the fractions to decimals.
3. Can you use benchmark fractions to quickly compare fractions?
Yes, benchmark fractions like 0, 1/2, and 1 can be used to quickly estimate and compare fractions. Estimate where each fraction falls relative to these benchmarks to make a quick comparison.
4. What is cross-multiplication, and how does it help compare fractions?
Cross-multiplication involves multiplying the numerator of one fraction by the denominator of the other fraction. Compare the results to determine which fraction is larger. If a/b and c/d are the fractions, compare ad and bc. If ad > bc, then a/b > c/d.
5. Is it easier to compare fractions as decimals?
For many people, converting fractions to decimals makes them easier to compare because decimals can be directly compared using standard decimal comparison techniques.
6. What should I do before comparing mixed numbers?
Before comparing mixed numbers, convert them to improper fractions. This simplifies the comparison process and allows you to use standard comparison methods.
7. What is the most common mistake when comparing fractions?
A common mistake is assuming that a larger denominator always means a larger fraction. Remember that the denominator represents the number of parts the whole is divided into, so a larger denominator actually means each part is smaller.
8. How does COMPARE.EDU.VN help in comparing fractions?
COMPARE.EDU.VN provides resources such as detailed explanations, interactive tools, and practice exercises to simplify the process of comparing fractions. These resources are designed to enhance understanding and improve comparison skills.
9. Where can I find more practice exercises for comparing fractions?
You can find more practice exercises on compare.edu.vn, which offers a variety of drills, problems, and real-world application questions to sharpen your fraction comparison skills.
10. Why is it important to simplify fractions before comparing them?
Simplifying fractions before comparing them reduces the complexity of the comparison process. Simplified fractions are easier to work with and minimize the risk of errors.