How Do You Compare Decimal Numbers Accurately And Easily?

Comparing decimal numbers involves determining which number has a greater value. It’s a fundamental skill in mathematics, applicable in various real-life situations, from calculating expenses to understanding scientific measurements. At COMPARE.EDU.VN, we simplify this process, providing comprehensive guides and tools for comparing decimal values, and making numerical comparisons straightforward. Master your decimal comparisons with our advice, which helps you easily differentiate values.

1. What Is Comparing Decimal Numbers?

Comparing decimal numbers is the process of determining which of two or more decimal numbers is larger or smaller in value. This involves examining the digits in each place value, starting from the left, to identify any differences that indicate a greater or lesser value. The concept applies to everyday situations like comparing prices in stores or measuring ingredients for cooking.

To accurately compare decimal numbers, follow these key steps:

• Align the Decimal Points: Ensure the decimal points of the numbers are aligned vertically. This helps to compare digits in the same place value (tenths, hundredths, thousandths, etc.).
• Compare Whole Number Parts: Start by comparing the whole number parts of the decimals. If they are different, the decimal with the larger whole number is the larger number. For example, 3.14 is greater than 2.89 because 3 is greater than 2.
• Compare Decimal Parts: If the whole number parts are the same, compare the digits in the tenths place, then the hundredths place, and so on, until a difference is found. For example, to compare 5.25 and 5.28, since the whole number (5) and the tenths place (2) are the same, compare the hundredths place. Since 8 is greater than 5, 5.28 is greater than 5.25.
• Add Trailing Zeros: If one decimal has fewer digits than another, add trailing zeros to the shorter decimal so that both decimals have the same number of digits. This makes the comparison easier without changing the value of the decimal. For example, to compare 4.5 and 4.57, rewrite 4.5 as 4.50. Now, it’s easier to see that 4.57 is greater than 4.50.
• Use a Number Line: Visualize the numbers on a number line to see which one is further to the right, indicating a greater value. This method is especially helpful for beginners to understand the relative values of decimal numbers.

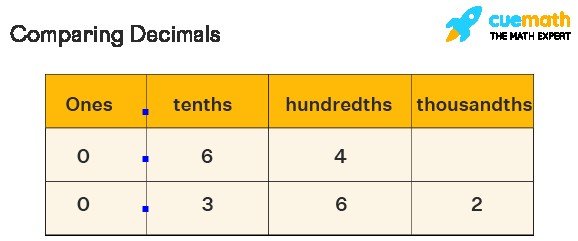
Understanding place value is crucial when comparing decimals. Each digit in a decimal number has a specific place value:

• Tenths: The first digit to the right of the decimal point (0.1)
• Hundredths: The second digit to the right of the decimal point (0.01)
• Thousandths: The third digit to the right of the decimal point (0.001)
• Ten-thousandths: The fourth digit to the right of the decimal point (0.0001)

Recognizing these place values helps in accurately comparing decimals by ensuring that digits in corresponding place values are compared correctly.

2. Why Is Comparing Decimal Numbers Important?

Comparing decimal numbers is essential for various reasons, both in academic contexts and in everyday life. Here’s why this skill is so vital:

Everyday Applications

• Financial Decisions: When shopping, comparing prices involves comparing decimal numbers to determine which product is cheaper. For example, comparing $3.25 per pound to $3.49 per pound helps you make cost-effective decisions.
• Cooking and Baking: Recipes often require precise measurements in decimal form. Comparing these measurements ensures accurate proportions. For example, a recipe might call for 2.5 cups of flour versus 2.75 cups, and understanding which is more is crucial for the recipe’s success.
• Calculating Distances and Measurements: In activities like measuring fabric for sewing or calculating distances on a map, comparing decimals ensures accuracy. For instance, knowing that 3.5 meters is longer than 3.25 meters is vital when cutting fabric.
• Understanding Scientific Data: Scientific measurements often involve decimals. Comparing these values is crucial for interpreting results. For example, comparing the pH levels of two solutions, such as 6.7 and 6.9, helps determine which is more acidic.

Academic and Professional Benefits

• Foundation for Advanced Math: Comparing decimals is a foundational skill for more advanced mathematical concepts like algebra, calculus, and statistics. Proficiency in this area makes it easier to grasp more complex topics.
• Problem Solving Skills: Mastering decimal comparison enhances critical thinking and problem-solving skills, which are valuable in many academic and professional fields.
• Exam Performance: Many standardized tests include questions that require comparing decimals. Being proficient in this skill can improve test scores.
• Career Opportunities: Various professions, such as engineering, finance, and science, require a strong understanding of decimal comparison for accurate calculations and analysis.

Real-World Examples

• Comparing Interest Rates: When choosing a savings account or loan, comparing interest rates (e.g., 2.25% vs. 2.5%) helps you determine the most financially beneficial option.
• Tracking Performance Metrics: In sports, comparing performance metrics like running times (e.g., 10.23 seconds vs. 10.25 seconds) helps athletes and coaches analyze and improve performance.
• Analyzing Survey Results: Interpreting survey data often involves comparing decimal values to draw meaningful conclusions. For example, comparing the percentage of respondents who agree with different statements, such as 65.2% vs. 65.8%, can reveal important trends.

By mastering the comparison of decimal numbers, you improve your mathematical skills and enhance your ability to make informed decisions in various aspects of life. Whether it’s managing personal finances, succeeding in academic pursuits, or excelling in a professional career, this fundamental skill is indispensable.

3. Step-By-Step Guide On How To Compare Decimal Numbers

3.1. Aligning Decimal Points

Aligning decimal points is the foundational step in accurately comparing decimal numbers. It ensures that digits with the same place value are lined up vertically, making it easier to compare them.

To align decimal points, write the numbers in a vertical column, ensuring that the decimal points are directly above each other. This arrangement helps you compare digits in the same place value, such as tenths, hundredths, and thousandths, without confusion.

Example:

Let’s align the decimal points for the numbers 4.25, 12.3, and 0.678:

   4.25
  12.3
   0.678

When the decimal points are aligned, it becomes clear which digits are in the same place value. In this example, the 2 in 4.25, the 3 in 12.3, and the 6 in 0.678 are all in the tenths place.

3.2. Comparing Whole Number Parts

After aligning the decimal points, the next step is to compare the whole number parts of the decimals. The whole number part is the portion of the number to the left of the decimal point.

If the whole number parts are different, the decimal with the larger whole number is the larger number overall. For example, if you are comparing 7.5 and 12.3, the whole number parts are 7 and 12, respectively. Since 12 is greater than 7, 12.3 is greater than 7.5.

If the whole number parts are the same, proceed to compare the decimal parts, as described in the next step.

3.3. Comparing Decimal Parts

When the whole number parts of the decimals are the same, the next step is to compare the decimal parts. Start by comparing the digits in the tenths place (the first digit to the right of the decimal point). If these digits are different, the decimal with the larger digit in the tenths place is the larger number.

For example, let’s compare 5.67 and 5.82. The whole number parts are both 5, so we move to the tenths place. The tenths digits are 6 and 8, respectively. Since 8 is greater than 6, 5.82 is greater than 5.67.

If the digits in the tenths place are the same, move to the hundredths place (the second digit to the right of the decimal point), and so on. Continue comparing digits in each place value until you find a difference. The decimal with the larger digit in the first differing place value is the larger number.

For example, let’s compare 3.456 and 3.459. The whole number parts are both 3, the tenths digits are both 4, and the hundredths digits are both 5. Moving to the thousandths place, we have 6 and 9. Since 9 is greater than 6, 3.459 is greater than 3.456.

3.4. Adding Trailing Zeros

Adding trailing zeros can simplify the comparison of decimal numbers, especially when the decimals have different numbers of digits. Trailing zeros are zeros added to the right of the last digit in the decimal part. Adding trailing zeros does not change the value of the decimal but makes it easier to compare the numbers.

To add trailing zeros, add zeros to the end of the decimal part of the shorter number until it has the same number of digits as the longer number.

Example:

Let’s compare 4.7 and 4.73. To make the comparison easier, add a trailing zero to 4.7, making it 4.70. Now, both decimals have the same number of digits:

   4.70
   4.73

It is now straightforward to compare 4.70 and 4.73. The whole number parts are the same (4), and the tenths digits are the same (7). Comparing the hundredths digits, 3 is greater than 0, so 4.73 is greater than 4.7.

Adding trailing zeros is especially helpful when comparing multiple decimal numbers with different numbers of decimal places. It ensures that all numbers have the same number of digits, making the comparison more straightforward and less prone to errors.

3.5. Using a Number Line

Using a number line is a visual method for comparing decimal numbers, especially useful for those who find it easier to understand numbers in a spatial context. A number line is a straight line on which numbers are placed at intervals proportional to their values.

To use a number line, draw a line and mark equal intervals. Place the decimal numbers on the number line according to their values. The number that is further to the right on the number line is the larger number.

For example, let’s compare 2.4 and 2.6 using a number line:

   2.4        2.6
    |----------|
   2.0  2.2  2.4  2.6  2.8  3.0

On the number line, 2.6 is to the right of 2.4, indicating that 2.6 is greater than 2.4.

This method is particularly helpful for comparing decimal numbers that are close in value. The number line provides a clear visual representation, making it easier to determine which number is larger.

4. Comparing Decimals And Fractions

When dealing with both decimals and fractions, it’s essential to convert them into a common format before comparing them. This usually involves converting fractions to decimals or vice versa. Here’s how to compare decimals and fractions effectively:

4.1. Converting Fractions to Decimals

To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number). This process gives you the decimal equivalent of the fraction, making it easier to compare with other decimal numbers.

For example, to convert the fraction 3/4 to a decimal, divide 3 by 4:

   3 ÷ 4 = 0.75

So, the decimal equivalent of 3/4 is 0.75. Once you have the decimal equivalent, you can easily compare it with other decimal numbers using the methods described earlier.

4.2. Comparing Converted Values

After converting all fractions to decimals, you can compare the numbers using the same techniques used for comparing decimals. Align the decimal points, compare the whole number parts, and then compare the decimal parts, adding trailing zeros if necessary.

Example:

Let’s compare 0.65 and 2/3. First, convert 2/3 to a decimal:

   2 ÷ 3 ≈ 0.6667

Now, compare 0.65 and 0.6667. Align the decimal points and compare the digits:

   0.6500
   0.6667

The whole number parts are the same (0), but the tenths digits are different (6 in both). Comparing the hundredths digits, 6 is greater than 5, so 0.6667 is greater than 0.65. Therefore, 2/3 is greater than 0.65.

Converting fractions to decimals allows you to easily compare different types of numbers using a consistent method. This skill is particularly useful in various real-life situations, such as comparing prices, measuring ingredients, and interpreting data.

5. Practical Examples Of Comparing Decimal Numbers

5.1. Comparing Prices While Shopping

When shopping, comparing prices that are in decimal form can help you make informed decisions and save money. Here are a few examples:

• Example 1: You are buying apples and see two options: one for $1.75 per pound and another for $1.69 per pound. To determine which is cheaper, compare the decimal numbers 1.75 and 1.69. The whole number parts are the same (1), but the tenths digits are different (7 and 6). Since 6 is less than 7, $1.69 per pound is the better deal.
• Example 2: You are comparing the prices of two different brands of cereal. Brand A costs $3.45 per box, and Brand B costs $3.50 per box. Comparing 3.45 and 3.50, the whole number parts are the same (3), but the tenths digits are different (4 and 5). Since 5 is greater than 4, Brand A at $3.45 is cheaper.

5.2. Measuring Ingredients In Cooking

In cooking, accurate measurements are crucial for the success of a recipe. Decimal numbers often appear in recipes, and comparing them ensures that you add the correct amounts:

• Example 1: A recipe calls for either 2.25 cups of flour or 2.3 cups of flour. To decide which measurement is more, compare 2.25 and 2.3. Align the decimal points and add a trailing zero to 2.3 to make it 2.30. Now, compare 2.25 and 2.30. The whole number parts are the same (2), but the tenths digits are different (2 and 3). Since 3 is greater than 2, 2.3 cups of flour is more than 2.25 cups.
• Example 2: You need to add either 1.5 teaspoons of salt or 1.75 teaspoons of salt to a dish. Compare 1.5 and 1.75. Add a trailing zero to 1.5 to make it 1.50. Comparing 1.50 and 1.75, the whole number parts are the same (1), but the tenths digits are different (5 and 7). Since 7 is greater than 5, 1.75 teaspoons of salt is more than 1.5 teaspoons.

5.3. Calculating Distances And Measurements

In various practical situations, such as construction or travel, comparing decimal numbers helps ensure accuracy in distances and measurements:

• Example 1: You are planning a road trip and have two possible routes. Route A is 125.75 miles long, and Route B is 125.5 miles long. To determine which route is shorter, compare 125.75 and 125.5. Add a trailing zero to 125.5 to make it 125.50. Comparing 125.75 and 125.50, the whole number parts are the same (125), but the tenths digits are different (7 and 5). Since 5 is less than 7, Route B at 125.5 miles is shorter.
• Example 2: You are cutting wood for a project and need a piece that is either 3.2 meters long or 3.25 meters long. Compare 3.2 and 3.25. Add a trailing zero to 3.2 to make it 3.20. Comparing 3.20 and 3.25, the whole number parts are the same (3), but the tenths digits are the same (2). Comparing the hundredths digits, 5 is greater than 0, so 3.25 meters is longer than 3.2 meters.

5.4. Understanding Scientific Data

In scientific fields, comparing decimal numbers is crucial for analyzing data and drawing accurate conclusions:

• Example 1: You are comparing the acidity of two solutions. Solution A has a pH of 6.7, and Solution B has a pH of 6.9. Compare 6.7 and 6.9. The whole number parts are the same (6), but the tenths digits are different (7 and 9). Since 9 is greater than 7, Solution B with a pH of 6.9 is less acidic.
• Example 2: You are measuring the growth of two plants. Plant A grew 4.55 cm in a week, and Plant B grew 4.5 cm in the same week. Compare 4.55 and 4.5. Add a trailing zero to 4.5 to make it 4.50. Comparing 4.55 and 4.50, the whole number parts are the same (4), but the tenths digits are the same (5). Comparing the hundredths digits, 5 is greater than 0, so Plant A grew more than Plant B.

6. Common Mistakes When Comparing Decimal Numbers

When comparing decimal numbers, several common mistakes can lead to incorrect conclusions. Being aware of these pitfalls can help you avoid errors and ensure accurate comparisons.

6.1. Ignoring Place Value

One of the most common mistakes is failing to consider the place value of each digit. Decimal numbers are composed of digits in different place values, such as tenths, hundredths, and thousandths. Ignoring these place values can lead to incorrect comparisons.

For example, consider comparing 0.3 and 0.08. Some might mistakenly think that 0.08 is greater because 8 is larger than 3. However, 0.3 is actually 0.30, and 30 hundredths is greater than 8 hundredths. Always ensure you are comparing digits in the same place value.

6.2. Not Aligning Decimal Points

Another frequent error is not aligning the decimal points when comparing numbers. Aligning decimal points is crucial because it ensures that you are comparing digits in the same place value.

For example, if you compare 4.25 and 12.3 without aligning the decimal points, you might incorrectly compare the digits. Aligning them vertically makes it clear that you should compare 4.25 with 12.30, which helps you see that 12.30 is larger.

6.3. Neglecting Trailing Zeros

Many people overlook the importance of trailing zeros when comparing decimals. Trailing zeros are zeros added to the right of the last digit in the decimal part. Adding trailing zeros does not change the value of the decimal but makes it easier to compare the numbers.

For example, when comparing 2.5 and 2.55, some might have difficulty seeing which number is larger. However, by adding a trailing zero to 2.5, making it 2.50, it becomes clear that 2.55 is greater than 2.50.

6.4. Misunderstanding Negative Decimals

Comparing negative decimals can be confusing because the rules are reversed compared to positive numbers. A negative number closer to zero is larger than a negative number farther from zero.

For example, when comparing -0.5 and -0.2, it is important to remember that -0.2 is greater than -0.5. This is because -0.2 is closer to zero on the number line.

6.5. Overlooking the Whole Number Part

Sometimes, people focus too much on the decimal part and overlook the whole number part, which is the portion of the number to the left of the decimal point. The whole number part can significantly affect the comparison, especially when it is different.

For example, when comparing 7.89 and 6.99, some might focus on the decimal parts (89 and 99) and mistakenly think that 6.99 is larger. However, the whole number part of 7.89 (7) is greater than the whole number part of 6.99 (6), so 7.89 is the larger number.

By being mindful of these common mistakes, you can improve your accuracy and confidence when comparing decimal numbers, whether in academic settings or everyday life.

7. Complex Scenarios For Comparing Decimals

7.1. Comparing Decimals With Repeating Patterns

Comparing decimals with repeating patterns, also known as recurring decimals, can be a bit more intricate. A repeating decimal is a decimal in which one or more digits repeat infinitely. Examples include 1/3 = 0.333… or 2/11 = 0.181818…

When comparing repeating decimals, it’s essential to look at the repeating pattern and extend the decimals to a sufficient number of places to accurately compare them.

Example:

Let’s compare 0.444… and 0.445. Although both decimals start with 0.44, the repeating pattern in the first decimal requires closer inspection.

To compare, extend the repeating decimal to a few more places:

• 0.444… becomes 0.44444
• 0.445 remains 0.44500

Now, compare the extended decimals:

   0.44444
   0.44500

The whole number and tenths and hundredths digits are the same. However, at the thousandths place, 5 is greater than 4, so 0.445 is greater than 0.444…

7.2. Comparing Decimals With Different Numbers Of Decimal Places

Decimals with different numbers of decimal places can sometimes be tricky to compare, especially when one decimal has very few digits compared to the other.

In such cases, it’s crucial to add trailing zeros to the shorter decimal so that both decimals have the same number of digits. This makes the comparison more straightforward and less prone to errors.

Example:

Let’s compare 2.7 and 2.689. To compare accurately, add trailing zeros to 2.7 to make it have the same number of decimal places as 2.689:

• 2.7 becomes 2.700

Now, compare the decimals:

   2.700
   2.689

The whole number parts are the same (2). Comparing the tenths digits, 7 is greater than 6, so 2.700 is greater than 2.689.

7.3. Comparing Decimals In Scientific Notation

Scientific notation is a way of expressing very large or very small numbers using powers of 10. Comparing decimals in scientific notation requires understanding the components of scientific notation and how they affect the value of the number.

A number in scientific notation is written as:

   a × 10^b

Where:

• a is a decimal number between 1 and 10 (the coefficient)
• b is an integer (the exponent)

When comparing numbers in scientific notation, first compare the exponents. The number with the larger exponent is the larger number. If the exponents are the same, compare the coefficients.

Example:

Let’s compare 3.2 × 10^5 and 5.1 × 10^4. First, compare the exponents:

• 10^5 is greater than 10^4

Therefore, 3.2 × 10^5 is greater than 5.1 × 10^4.

If the exponents are the same, compare the coefficients:

Example:

Let’s compare 2.5 × 10^3 and 2.8 × 10^3. The exponents are the same (10^3), so compare the coefficients:

• 2.8 is greater than 2.5

Therefore, 2.8 × 10^3 is greater than 2.5 × 10^3.

7.4. Comparing Decimals In Different Units

Sometimes, you may need to compare decimals that are expressed in different units. In such cases, it’s essential to convert the numbers to the same unit before comparing them.

Example:

Let’s compare 1.5 meters and 160 centimeters. To compare, convert both measurements to the same unit. Since 1 meter = 100 centimeters, convert 1.5 meters to centimeters:

   1.  5 meters = 1.5 × 100 = 150 centimeters

Now, compare 150 cm and 160 cm:

• 160 is greater than 150

Therefore, 160 centimeters is greater than 1.5 meters.

These complex scenarios require careful attention to detail and a thorough understanding of decimal numbers and their properties. By following these guidelines, you can confidently compare decimals in any situation.

8. Tools And Resources For Learning To Compare Decimal Numbers

8.1. Online Calculators And Converters

Online calculators and converters are invaluable tools for learning and practicing How To Compare Decimal Numbers. These resources provide quick and accurate results, helping you verify your work and understand the underlying concepts.

• Decimal Comparison Calculators: These calculators allow you to enter two or more decimal numbers and instantly determine which is larger. They often show the steps involved in the comparison, providing a clear understanding of the process.
• Fraction to Decimal Converters: These converters help you convert fractions to decimals, allowing you to compare fractions and decimals on an equal footing.
• Unit Converters: Unit converters enable you to convert measurements from one unit to another, ensuring that you are comparing decimals in the same units.

8.2. Educational Websites And Apps

Numerous educational websites and apps offer lessons, exercises, and interactive games to help you master comparing decimal numbers:

• Khan Academy: Khan Academy provides comprehensive math lessons, including detailed explanations and practice exercises for comparing decimals. Their interactive format makes learning engaging and effective.
• Cuemath: Cuemath offers personalized math learning experiences with certified experts, providing tailored instruction and practice on comparing decimals.
• Math Games: Math Games offers a variety of fun and interactive games that help you practice comparing decimals in an engaging way.
• SplashLearn: SplashLearn provides a range of interactive math games and worksheets designed to help students learn and practice comparing decimals.

8.3. Worksheets And Practice Exercises

Worksheets and practice exercises are essential for reinforcing your understanding of comparing decimal numbers:

• Printable Worksheets: Many websites offer printable worksheets with a variety of exercises on comparing decimals. These worksheets often include answer keys, allowing you to check your work.
• Online Quizzes: Online quizzes provide immediate feedback on your performance, helping you identify areas where you need more practice.
• Textbooks and Study Guides: Math textbooks and study guides typically include chapters on decimals, with explanations and practice problems on comparing decimal numbers.

8.4. Visual Aids

Visual aids can be particularly helpful for those who learn best through visual methods:

• Number Lines: Number lines provide a visual representation of the relative values of decimal numbers, making it easier to compare them.
• Place Value Charts: Place value charts help you understand the place value of each digit in a decimal number, ensuring that you are comparing digits in the same place value.
• Diagrams and Illustrations: Diagrams and illustrations can help you visualize the concept of comparing decimals, making it easier to understand the underlying principles.

By leveraging these tools and resources, you can enhance your understanding of comparing decimal numbers and develop the skills necessary to confidently tackle any comparison problem.

9. Test Your Knowledge: Quiz On Comparing Decimal Numbers

Test your knowledge with these questions on how to compare decimal numbers:

1. Which is greater: 0.75 or 0.7?
2. Compare 2.35 and 2.350. Are they equal?
3. Which is smaller: 1.2 or 1.19?
4. Compare 0.666… and 0.67. Which is greater?
5. Which is greater: -0.4 or -0.3?

Answers:

1. 0. 75
2. Equal
3. 1. 19
4. 0. 67
5. -0.3

10. Conclusion: Mastering Decimal Comparisons For Everyday Success

Mastering the art of comparing decimal numbers is a crucial skill that extends far beyond the classroom. As we’ve explored, this fundamental ability plays a significant role in various aspects of everyday life, from making informed purchasing decisions to accurately measuring ingredients for a perfect recipe.

Throughout this guide, we’ve covered essential techniques such as aligning decimal points, comparing whole number parts, adding trailing zeros, and utilizing visual aids like number lines. We’ve also addressed common mistakes and delved into complex scenarios involving repeating decimals and scientific notation. By understanding these concepts and practicing diligently, you can enhance your numerical literacy and improve your problem-solving skills.

Remember, the ability to confidently compare decimals empowers you to make smarter choices, whether you’re shopping for groceries, managing your finances, or analyzing scientific data. So, embrace the knowledge and tools provided in this comprehensive guide, and unlock your potential for success in both academic and practical endeavors.

For further assistance and more comprehensive comparison tools, visit COMPARE.EDU.VN. Our platform offers a wide range of resources to help you make informed decisions in all areas of life. Whether you’re comparing products, services, or ideas, COMPARE.EDU.VN provides the detailed comparisons you need to choose wisely. Don’t hesitate to reach out with any questions or explore additional topics on our website.

COMPARE.EDU.VN
333 Comparison Plaza,
Choice City, CA 90210,
United States
Whatsapp: +1 (626) 555-9090
Website: compare.edu.vn

Frequently Asked Questions (FAQs) About Comparing Decimal Numbers

How do you compare decimals?

To compare decimals, align the decimal points vertically, compare the whole number parts first, then compare the digits in each decimal place (tenths, hundredths, thousandths, etc.) from left to right until you find a difference. The decimal with the larger digit in the first differing place value is the larger number. If one decimal has fewer digits than another, add trailing zeros to the shorter decimal to make the comparison easier.

What are the rules for comparing decimals?

The rules for comparing decimals include:

1. Align the decimal points vertically.
2. Compare the whole number parts.
3. If the whole number parts are equal, compare the digits in the tenths place, then the hundredths place, and so on.
4. Add trailing zeros to decimals with fewer digits to make the comparison easier.
5. For negative decimals, the number closer to zero is larger.

How to compare decimals and fractions?

To compare decimals and fractions, convert the fraction to a decimal by dividing the numerator by the denominator. Then, compare the resulting decimal with the other decimals using the standard methods for comparing decimals.

How to compare decimals from least to greatest?

To compare decimals from least to greatest, follow these steps:

1. Align the decimal points vertically.
2. Compare the whole number parts. The number with the smallest whole number is the smallest.
3. If the whole number parts are equal, compare the digits in the tenths place, then the hundredths place, and so on.
4. Arrange the decimals in ascending order based on these comparisons.

How to compare decimals on a number line?

To compare decimals on a number line, plot the decimals on the line. The decimal that is further to the right is the larger number. This provides a visual way to compare decimal values.

How to compare decimals to hundredths place?

To compare decimals to the hundredths place, align the decimal points and compare the whole number parts first. If they are the same, compare the tenths place. If the tenths places are also the same, compare the hundredths place. The decimal with the larger digit in the hundredths place is the larger number.

How to compare decimals to thousandths place?

To compare decimals to the thousandths place, follow the same steps as comparing to the hundredths place, but continue to the thousandths place if the whole number, tenths, and hundredths places are all equal. The decimal with the larger digit in the thousandths place is the larger number.