Are you looking to understand How To Compare And Order Numbers effectively? This guide on COMPARE.EDU.VN provides a detailed explanation, offering methods for number comparison and sequencing, from simple integers to more complex rational numbers, ensuring you grasp the concepts of numerical order and magnitude. Dive in to master the art of number comparison and sequencing!
1. Understanding Number Comparison
1.1. What Does Comparing Numbers Mean?
Comparing numbers involves determining the relative size of two or more numerical values. It establishes whether one number is equal to, less than, or greater than another. This foundational mathematical operation is crucial for various applications, from everyday decision-making to advanced scientific analysis. Understanding how numbers relate to each other provides a basis for more complex mathematical concepts.
1.2. The Importance of Comparing Numbers
Comparing numbers is a fundamental skill with wide-ranging applications. In daily life, it helps us determine the best deals while shopping, manage our finances, and understand statistics. Academically, it supports understanding mathematical relationships and problem-solving. Professionally, it is essential in fields such as finance, engineering, and data analysis, where accurate comparisons are critical for informed decision-making.
1.3. Methods for Comparing Numbers
Several methods exist for comparing numbers, each suited to different situations and number types:
- Number Line: Visualizing numbers on a number line provides an intuitive understanding of their order. Numbers to the right are greater, and numbers to the left are smaller.
- Counting: For small whole numbers, counting is a simple and direct method.
- Digit Comparison: When comparing numbers with multiple digits, start by comparing the digits in the highest place value. If they are the same, move to the next place value to the right until a difference is found.
- Place Value Analysis: Breaking down numbers by their place values (ones, tens, hundreds, etc.) allows for a systematic comparison.
2. Deciphering Number Ordering
2.1. What is Number Ordering?
Ordering numbers refers to arranging a set of numbers in a specific sequence based on their values. The two primary types of ordering are:
- Ascending Order: Arranging numbers from the smallest to the largest.
- Descending Order: Arranging numbers from the largest to the smallest.
2.2. Ascending Order Explained
Ascending order, also known as increasing order, involves arranging numbers from the smallest to the largest. This method is commonly used to organize data in an easily readable format, making it simpler to identify minimum and maximum values within a dataset.
2.3. Descending Order Explained
Descending order, also known as decreasing order, involves arranging numbers from the largest to the smallest. This method is useful for prioritizing tasks, ranking items by importance, or analyzing data where the highest values are of primary interest.
2.4. Practical Applications of Number Ordering
Number ordering is essential in various fields. In computer science, it is used in sorting algorithms. In statistics, it helps in data analysis and interpretation. In everyday life, it is used in organizing lists, managing schedules, and prioritizing tasks.
3. Step-by-Step Guide to Comparing Numbers
To effectively compare numbers, follow these steps:
3.1. Step 1: Comparing the Number of Digits
The first step in comparing numbers is to examine the number of digits each number contains. Generally, a number with more digits is larger than a number with fewer digits. This is particularly useful when comparing whole numbers or integers.
3.2. Step 2: Comparing Higher Place Values
If the numbers have the same number of digits, the next step is to compare the digits in the highest place value (e.g., hundreds, thousands, etc.). The number with the larger digit in the highest place value is the greater number.
3.3. Step 3: Comparing Digits in the Next Place Value to the Right
If the digits in the highest place value are the same, move to the next place value to the right and compare those digits. Continue this process until you find a place value where the digits differ.
3.4. Step 4: Identifying the Greater Number
Once you find a place value where the digits differ, the number with the higher digit in that place value is the greater number. This step completes the comparison process, allowing you to determine the relationship between the numbers.
4. Essential Symbols for Comparing Numbers
To express the relationship between numbers, we use specific symbols:
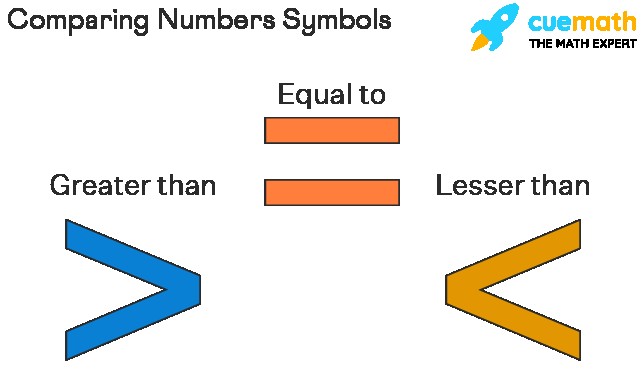
4.1. Greater Than (>)
The “greater than” symbol (>) indicates that the number on the left side of the symbol is larger than the number on the right side. For example, 5 > 3 means “5 is greater than 3.”
4.2. Less Than (<)
The “less than” symbol (<) indicates that the number on the left side of the symbol is smaller than the number on the right side. For example, 2 < 9 means “2 is less than 9.”
4.3. Equal To (=)
The “equal to” symbol (=) indicates that the numbers on both sides of the symbol have the same value. For example, 4 = 4 means “4 is equal to 4.”
4.4. Mnemonic Devices for Remembering Symbols
To easily remember the “less than” and “greater than” symbols, visualize them as an alligator’s mouth: the alligator always wants to eat the bigger number. Thus, the open side of the symbol always faces the larger number.
5. In-Depth Look at Comparing and Ordering Numbers
5.1. Definition of Ascending Order
Ascending order is the arrangement of numbers from the smallest to the largest. This order is intuitive and is used in various applications, such as organizing lists or datasets.
5.2. Definition of Descending Order
Descending order is the arrangement of numbers from the largest to the smallest. This order is useful for ranking items, prioritizing tasks, or identifying maximum values.
5.3. Practical Examples of Ascending and Descending Order
Ascending Order Example:
Consider the numbers 3, 1, 4, 1, 5, 9, 2, 6. Arranging these in ascending order gives: 1 < 1 < 2 < 3 < 4 < 5 < 6 < 9.
Descending Order Example:
Using the same numbers, arranging them in descending order gives: 9 > 6 > 5 > 4 > 3 > 2 > 1 > 1.
6. Mastering the Comparison of Rational Numbers
6.1. What are Rational Numbers?
Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero. Examples include 1/2, -3/4, and 5.
6.2. Converting to Like Fractions
To compare rational numbers, convert them into like fractions, which have the same denominator. This is done by finding the least common multiple (LCM) of the denominators and adjusting the numerators accordingly.
6.3. Comparing Numerators
Once the rational numbers have the same denominator, compare their numerators. The rational number with the larger numerator is the greater number.
6.4. Key Points to Remember
- Negative rational numbers are always less than 0.
- Positive rational numbers are always greater than 0.
- Positive rational numbers are always greater than negative rational numbers.
6.5. Step-by-Step Example
Let’s compare 2/3 and 6/7:
- Find the LCM of the denominators: LCM(3, 7) = 21.
- Convert the fractions:
- 2/3 = (2 × 7) / (3 × 7) = 14/21
- 6/7 = (6 × 3) / (7 × 3) = 18/21
- Compare the numerators: 18 > 14, so 18/21 > 14/21.
Therefore, 6/7 > 2/3.
7. Practical Examples of Comparing and Ordering Numbers
7.1. Example 1: Comparing Prices
Steffy wants to buy a microwave oven for her mom and finds two options with the same features, priced at $250 and $252. Which oven should she buy?
To find the best deal, compare the prices:
| Place Value | $250 Face Values | Comparison | $252 Face Values |
|---|---|---|---|
| Hundreds | 2 | = | 2 |
| Tens | 5 | = | 5 |
| Units | 0 | < | 2 |

Since $250 < $252, Steffy should buy the microwave oven priced at $250.
7.2. Example 2: Prioritizing Purchases
Megan has $40 and wants to buy items worth $57. She needs to return the most expensive item. Which item should she return?
| Item | Price |
|---|---|
| Noodles | $5 |
| Chocolate | $18 |
| Corn Flakes | $7 |
| Tea | $6 |
| Oil | $9 |
| Coffee | $12 |
| Total | $57 |
To find the most expensive item, arrange the prices in ascending order: $5, $6, $7, $9, $12, $18.
Chocolate is the most expensive item at $18, so Megan should return the chocolate.
7.3. Example 3: Ordering Integers
Arrange the following numbers in descending order: -10, 3, -4, 0, -8, 4, 2, -1.
- Separate the numbers into positive, negative, and zero:
- Negative numbers: -10, -4, -8, -1
- Positive numbers: 3, 4, 2
- Zero: 0
- Compare the negative numbers: -1 > -4 > -8 > -10
- Compare the positive numbers: 4 > 3 > 2
- Combine the ordered lists: 4 > 3 > 2 > 0 > -1 > -4 > -8 > -10
Therefore, the list in descending order is: 4 > 3 > 2 > 0 > -1 > -4 > -8 > -10.
8. Practical Exercises for Skill Reinforcement
8.1. Exercise 1: Arranging Temperatures in Ascending Order
Task: Arrange the following temperatures in ascending order: 25°C, 15°C, 30°C, 20°C, 22°C.
8.2. Exercise 2: Ordering Account Balances in Descending Order
Task: A business has the following account balances: $5000, $2500, $7500, $1000, $3000. Arrange these balances in descending order to identify the accounts with the highest and lowest funds.
9. Frequently Asked Questions (FAQs) on Comparing and Ordering Numbers
9.1. What Is Comparing Numbers In Math?
Comparing numbers involves assessing the relative value of two or more numbers to determine if one is equal to, less than, or greater than the others.
9.2. What Is The Rule For Comparing Numbers?
The primary rule for comparing numbers is to first compare the number of digits. If the numbers have the same number of digits, compare the digits in the highest place value. Continue comparing digits from left to right until a difference is found.
9.3. Why Is Comparing Numbers Important In Real Life?
Comparing numbers is crucial for making informed decisions in everyday situations, such as comparing prices, managing finances, understanding statistics, and optimizing resource allocation.
9.4. What Is Comparing and Ordering Numbers?
Comparing and ordering numbers is a two-step process that involves first determining the relative values of numbers and then arranging them in a specific sequence, either ascending or descending.
9.5. How Do You Compare Whole Numbers?
Whole numbers can be compared using a number line or by comparing their digits from left to right. If the number of digits differs, the number with more digits is larger.
9.6. What Is The Difference Between Comparing and Ordering Numbers?
Comparing numbers is the process of identifying whether one number is greater than, less than, or equal to another. Ordering numbers involves arranging a set of numbers in a specific sequence based on their values.
9.7. How To Do Comparing Numbers?
Numbers can be compared by examining the number of digits, using a number line, or comparing the digits in each place value. The method depends on the type of numbers being compared (e.g., integers, rational numbers, decimals).
10. Conclusion: Mastering Number Comparison for Informed Decisions
Understanding how to compare and order numbers is a foundational skill that enhances decision-making in various aspects of life. By mastering the methods discussed, from simple integer comparisons to complex rational number ordering, you gain the ability to analyze and interpret numerical data effectively. Whether you’re a student, a professional, or someone looking to improve their financial literacy, these skills are invaluable.
Ready to apply your newfound knowledge? Visit COMPARE.EDU.VN to find more resources and practical comparison tools that will help you make informed decisions every day.
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
WhatsApp: +1 (626) 555-9090
Website: COMPARE.EDU.VN
Empower yourself with the ability to compare, order, and make smarter choices. Start your journey at compare.edu.vn today!