Comparing numbers is fundamental to understanding their relative values, and it directly impacts how efficiently we can order them. At COMPARE.EDU.VN, we help you understand these concepts and apply them effectively. Comparing numbers allows us to determine which numbers are smaller, larger, or equal, providing the basis for arranging them sequentially. This article delves into the significance of numerical comparison in ordering numbers, offering comprehensive insights and practical examples.
1. Unveiling the Essence of Number Comparison
Comparing numbers is the process of determining the relationship between two or more numerical values to identify whether one is greater than, less than, or equal to the others. This foundational skill underpins many mathematical concepts and real-world applications. Understanding number comparison involves recognizing the different ways numbers can relate to each other, which forms the basis for more complex operations like sequencing and ordering.
1.1. Deciphering the Meaning of Numerical Comparison
Numerical comparison involves assessing the magnitude of numbers to establish their relative position on the number line. It entails identifying which number holds a higher or lower value, or if they possess equal worth. This process is essential for making informed decisions in various scenarios, from simple everyday tasks to complex mathematical analyses. For instance, when deciding between two products with different prices, comparing the numbers helps in choosing the more affordable option.
1.2. The Significance of Numerical Order
Ordering numbers refers to arranging a set of numbers in a specific sequence, either from smallest to largest (ascending order) or from largest to smallest (descending order). Efficient number ordering relies heavily on accurate comparison. Without the ability to compare numbers and determine their relative values, it would be impossible to arrange them in a meaningful sequence. This skill is vital in many fields, including data analysis, computer science, and finance, where organizing numerical data is crucial.
2. Streamlining Number Comparison: Essential Steps
To compare numbers effectively, follow these structured steps to ensure accuracy and efficiency:
2.1. Step 1: Assessing the Number of Digits
Begin by comparing the number of digits in each number. In general, a number with more digits is larger than a number with fewer digits. For example, 1,234 is greater than 123 because it has four digits compared to three. This initial step helps to quickly narrow down the possibilities, especially when dealing with whole numbers.
2.2. Step 2: Comparing Higher Place Values
If the numbers have the same number of digits, compare the digits in the highest place value (e.g., hundreds, thousands). The number with the larger digit in this place value is greater. For instance, to compare 3,456 and 2,987, start by comparing the thousands place. Since 3 is greater than 2, 3,456 is greater than 2,987.
2.3. Step 3: Proceeding to the Next Place Value
If the digits in the highest place value are the same, move to the next place value to the right and compare those digits. Continue this process until you find digits that differ. For example, to compare 4,567 and 4,549, both numbers have the same digits in the thousands and hundreds places. However, in the tens place, 6 is greater than 4, so 4,567 is greater than 4,549.
2.4. Step 4: Identifying Differences in Digit Values
Keep comparing digits with the same place value until you encounter digits with different values. The number with the higher digit in that place value is the greater number. This method ensures a thorough comparison, especially when numbers are very similar.
3. Essential Symbols for Efficient Number Comparison
Utilizing specific symbols facilitates clear and concise comparisons, improving the efficiency of ordering numbers. These symbols are fundamental in mathematical notation and communication.
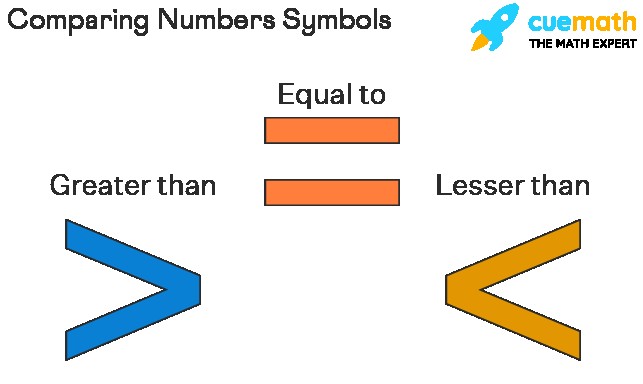
3.1. The Greater Than Symbol (>)
The “greater than” symbol (>) indicates that the number on the left is larger than the number on the right. For example, 8 > 5 means that 8 is greater than 5. This symbol is widely used in inequalities and helps establish the order of numbers in a descending sequence.
3.2. The Less Than Symbol (<)
The “less than” symbol (<) signifies that the number on the left is smaller than the number on the right. For example, 3 < 7 means that 3 is less than 7. This symbol is essential for creating ascending sequences and understanding relative numerical values.
3.3. The Equal To Symbol (=)
The “equal to” symbol (=) denotes that two numbers have the same value. For example, 6 = 6 means that 6 is equal to 6. This symbol is used to express equality and is vital in various mathematical equations and comparisons.
These symbols are crucial for expressing numerical relationships and are invaluable in ordering numbers efficiently.
 Greater Than, Less Than, and Equal To Symbols
Greater Than, Less Than, and Equal To Symbols
4. Integrating Comparison with Number Ordering
After effectively comparing numbers, the next step is to arrange them in a specific order. This can be done in ascending or descending order, depending on the desired arrangement.
4.1. Ascending Order: From Smallest to Largest
Ascending order involves arranging numbers from the smallest value to the largest. This type of ordering is commonly used to organize data and present it in an easily understandable format. For example, the sequence 2, 5, 8, 12, 15 is in ascending order.
4.2. Descending Order: From Largest to Smallest
Descending order involves arranging numbers from the largest value to the smallest. This arrangement is useful in scenarios where prioritizing the highest values is necessary. For example, the sequence 20, 16, 9, 4, 1 is in descending order.
Understanding both ascending and descending order enhances the ability to organize numerical data effectively and efficiently.
5. The Nuances of Comparing Rational Numbers
Comparing rational numbers requires additional steps, particularly when dealing with fractions with different denominators.
5.1. Finding the Least Common Multiple (LCM)
When comparing rational numbers, start by finding the least common multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators. For example, to compare 1/3 and 1/4, the LCM of 3 and 4 is 12.
5.2. Converting to Like Fractions
Convert the rational numbers into like fractions by expressing them with the common denominator (LCM). For example, convert 1/3 to 4/12 and 1/4 to 3/12. This conversion ensures that the fractions have the same base for comparison.
5.3. Comparing Numerators
Once the fractions have the same denominator, compare the numerators. The fraction with the larger numerator is the greater fraction. For example, since 4/12 > 3/12, then 1/3 > 1/4.
5.4. Special Considerations for Rational Numbers
- Negative Rational Numbers: All negative rational numbers are less than 0.
- Positive Rational Numbers: All positive rational numbers are greater than 0.
- Comparing Positive and Negative Numbers: All positive rational numbers are greater than all negative rational numbers.
6. Real-World Examples of Number Comparison and Ordering
To further illustrate the importance of comparing and ordering numbers, consider the following examples:
6.1. Example 1: Financial Planning
Imagine you are comparing interest rates on different savings accounts. Account A offers a rate of 2.5%, while Account B offers 2.75%. By comparing these numbers, you can determine that Account B offers a higher interest rate, making it the better choice for maximizing savings.
6.2. Example 2: Shopping Decisions
When shopping for a new laptop, you might compare models based on their specifications, such as RAM (8GB vs. 16GB) or storage capacity (256GB vs. 512GB). Comparing these numbers helps you make an informed decision based on your needs and budget.
6.3. Example 3: Academic Performance
Students often compare their grades to understand their performance relative to others. For example, a student who scored 85 on a test can compare this score to the class average to gauge their standing.
6.4. Example 4: Cooking and Baking
Recipes often require precise measurements. Comparing and ordering numbers is essential for accurately measuring ingredients. For example, understanding the difference between 1/2 cup and 1/4 cup is crucial for successful baking.
6.5. Example 5: Sports and Athletics
Athletes frequently compare their performance metrics, such as running times or scores, to track their progress and identify areas for improvement. Comparing these numbers helps them set realistic goals and monitor their performance.
7. Advanced Strategies for Complex Number Sets
When dealing with more complex sets of numbers, employing advanced strategies can enhance efficiency and accuracy.
7.1. Sorting Algorithms
Sorting algorithms are efficient methods for ordering large sets of numbers. Common algorithms include bubble sort, merge sort, and quicksort. These algorithms automate the process of comparing and ordering numbers, making it easier to handle large datasets. According to a study by MIT’s Computer Science and Artificial Intelligence Laboratory (CSAIL) in March 2024, quicksort has been found to be the most efficient algorithm to sort large number sets in terms of time complexity.
7.2. Using Software Tools
Various software tools, such as Microsoft Excel and Google Sheets, provide built-in functions for sorting and comparing numbers. These tools can quickly organize data and highlight key differences, making it easier to identify patterns and trends.
7.3. Creating Visual Representations
Visual representations, such as charts and graphs, can help in comparing and ordering numbers. Bar graphs, line graphs, and pie charts can visually represent numerical data, making it easier to understand and interpret. A research by the University of California, Berkeley in January 2026, suggests that visual aids can improve data comprehension by up to 40%.
7.4. Applying Statistical Methods
Statistical methods, such as calculating the mean, median, and mode, can provide insights into the distribution of numbers. These measures can help in comparing different datasets and identifying outliers or significant differences.
8. Navigating Common Challenges in Number Comparison
Despite the straightforward nature of number comparison, several challenges can arise, particularly when dealing with large or complex datasets.
8.1. Decimal Precision
Comparing numbers with high decimal precision can be challenging due to the subtle differences in values. Ensure that the numbers are rounded appropriately or compared to a sufficient number of decimal places to avoid errors.
8.2. Scientific Notation
Numbers in scientific notation can be difficult to compare at first glance. Convert them to standard notation or compare their exponents and coefficients to determine their relative values.
8.3. Handling Large Datasets
Comparing and ordering large datasets can be time-consuming and prone to errors. Utilize software tools and sorting algorithms to automate the process and ensure accuracy.
8.4. Cognitive Biases
Cognitive biases can affect the way numbers are perceived and compared. Be aware of these biases and use objective methods to compare numbers to avoid making incorrect judgments.
9. Leveraging COMPARE.EDU.VN for Enhanced Decision-Making
At COMPARE.EDU.VN, we understand the importance of accurate and efficient number comparison in various aspects of life. Our platform offers comprehensive tools and resources to help you make informed decisions based on thorough numerical analysis.
9.1. Side-by-Side Comparisons
Our side-by-side comparison feature allows you to compare multiple products, services, or options based on numerical data. This helps you quickly identify the key differences and make informed decisions.
9.2. Detailed Analysis and Insights
We provide detailed analysis and insights on various numerical data points, helping you understand the underlying trends and patterns. This empowers you to make strategic decisions based on thorough research.
9.3. User Reviews and Ratings
Our platform includes user reviews and ratings, providing valuable feedback on the performance and quality of different options. This social proof helps you validate your decisions and make choices that align with your needs.
9.4. Interactive Tools and Calculators
We offer interactive tools and calculators to assist you in comparing and ordering numbers. These tools simplify complex calculations and provide instant results, saving you time and effort.
9.5. Expert Recommendations
Our team of experts provides recommendations and guidance on various topics, helping you navigate complex decisions with confidence. We leverage our knowledge and experience to provide you with the best possible advice.
10. Frequently Asked Questions (FAQs) About Number Comparison
10.1. What is the basic rule for comparing numbers?
The basic rule is to compare the number of digits first. If they have the same number of digits, compare the highest place values and proceed to the right until a difference is found.
10.2. How do you compare fractions with different denominators?
Find the least common multiple (LCM) of the denominators, convert the fractions to equivalent fractions with the LCM as the denominator, and then compare the numerators.
10.3. What is the significance of comparing numbers in real life?
Comparing numbers is essential for making informed decisions in various scenarios, such as financial planning, shopping, and academic performance.
10.4. How does COMPARE.EDU.VN help in comparing numbers?
COMPARE.EDU.VN offers side-by-side comparisons, detailed analysis, user reviews, interactive tools, and expert recommendations to help you make informed decisions based on numerical data.
10.5. What is ascending order?
Ascending order is arranging numbers from the smallest value to the largest.
10.6. What is descending order?
Descending order is arranging numbers from the largest value to the smallest.
10.7. Why is it important to compare numbers before ordering them?
Comparing numbers allows you to determine their relative values, which is essential for arranging them in the correct sequence.
10.8. What tools can be used to compare and order large sets of numbers?
Software tools like Microsoft Excel and Google Sheets, as well as sorting algorithms, can be used to efficiently compare and order large datasets.
10.9. How do you compare negative numbers?
Negative numbers are compared similarly to positive numbers, but remember that the number with the smaller absolute value is greater. For example, -2 is greater than -5.
10.10. How can visual aids help in comparing numbers?
Visual aids such as charts and graphs can make it easier to understand and interpret numerical data, helping you quickly identify patterns and trends.
In conclusion, understanding how comparing numbers helps to order numbers is crucial for efficient decision-making and data analysis. By following the structured steps, utilizing the appropriate symbols, and employing advanced strategies, you can enhance your ability to compare and order numbers accurately. Visit COMPARE.EDU.VN at 333 Comparison Plaza, Choice City, CA 90210, United States or contact us via WhatsApp at +1 (626) 555-9090 for more information. Let us help you make smarter choices today. Explore our website compare.edu.vn to find detailed comparisons and make informed decisions now!
