Comparing fractions with different numerators and denominators can seem tricky, but it’s a fundamental skill in mathematics and everyday life. At COMPARE.EDU.VN, we provide comprehensive guides and tools to simplify this process, ensuring you can confidently determine which fraction is larger or smaller, enhancing your mathematical understanding and decision-making abilities. Learn about equivalent fractions, cross multiplication and least common multiple.
1. Understanding the Basics of Fractions
Before diving into comparing fractions with different numerators and denominators, it’s essential to understand what a fraction represents. A fraction is a part of a whole, consisting of two main components:
- Numerator: The number above the fraction bar, indicating how many parts of the whole are being considered.
- Denominator: The number below the fraction bar, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 3/4, “3” is the numerator, representing three parts, and “4” is the denominator, representing the whole being divided into four equal parts. Understanding these components is crucial before attempting to compare different fractions.
1.1. What Is a Fraction?
A fraction represents a part of a whole or, more generally, any number of equal parts. It consists of two numbers: the numerator (top number) and the denominator (bottom number), separated by a fraction bar. For example, in the fraction ½, 1 is the numerator and 2 is the denominator. This fraction represents one part out of two equal parts. Fractions can represent parts of a single object, parts of a group of objects, or a ratio.
1.2. Types of Fractions
Fractions come in several types, each with its own characteristics:
- Proper Fractions: The numerator is less than the denominator (e.g., 2/3).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 5/3).
- Mixed Numbers: A whole number combined with a proper fraction (e.g., 1 2/3).
- Equivalent Fractions: Fractions that represent the same value but have different numerators and denominators (e.g., 1/2 and 2/4).
Understanding these types is essential when comparing fractions, as different rules and methods may apply.
2. Why Comparing Fractions Is Important
Comparing fractions is not just a theoretical exercise; it has practical applications in everyday life. Whether you are adjusting a recipe, managing finances, or understanding data, knowing how to compare fractions can help you make informed decisions.
2.1. Real-World Applications
- Cooking: Adjusting ingredient quantities in recipes often involves comparing fractions. For example, if a recipe calls for 2/3 cup of flour and you want to make half the recipe, you need to calculate half of 2/3.
- Finances: Understanding fractions is crucial when dealing with percentages, discounts, and financial ratios. For example, comparing interest rates that are expressed as fractions or percentages helps in making informed investment decisions.
- Construction and Measurement: Many construction and measurement tasks require comparing fractions of inches, feet, or meters. Knowing which fraction is larger or smaller is essential for accurate cuts and fits.
- Data Analysis: Fractions and ratios are used to represent and compare data. Understanding how to compare these fractions allows for accurate interpretation and analysis.
2.2. Importance in Mathematics
Comparing fractions is a fundamental skill that builds the foundation for more advanced mathematical concepts. Proficiency in comparing fractions is essential for understanding:
- Ratios and Proportions: Comparing fractions directly relates to understanding ratios and proportions.
- Algebra: Many algebraic equations involve fractions, and the ability to compare and manipulate them is crucial for solving these equations.
- Calculus: Concepts like limits and derivatives often involve fractions, making a solid understanding of fraction comparison essential.
3. Comparing Fractions with the Same Denominator
Comparing fractions with the same denominator is straightforward. When fractions share a common denominator, the fraction with the larger numerator is the larger fraction.
3.1. The Basic Rule
When fractions have the same denominator, comparing them is simple: the fraction with the larger numerator is the greater fraction. For example, consider the fractions 3/7 and 5/7. Both fractions have the same denominator (7), so we compare the numerators (3 and 5). Since 5 is greater than 3, 5/7 is greater than 3/7.
3.2. Examples and Illustrations
Example 1:
Compare 2/9 and 7/9.
Both fractions have the same denominator (9). Comparing the numerators, 7 is greater than 2. Therefore, 7/9 > 2/9.
Example 2:
Compare 11/15 and 8/15.
Both fractions have the same denominator (15). Comparing the numerators, 11 is greater than 8. Therefore, 11/15 > 8/15.
3.3. Common Mistakes to Avoid
A common mistake when comparing fractions with the same denominator is focusing on the denominator instead of the numerator. Remember, the denominator indicates the number of equal parts the whole is divided into, but the numerator tells you how many of those parts you have. Always compare the numerators to determine which fraction is larger.
4. Comparing Fractions with Different Denominators
Comparing fractions with different denominators requires an additional step: finding a common denominator. Once the fractions have a common denominator, they can be easily compared by looking at their numerators.
4.1. Finding a Common Denominator
The most common method for finding a common denominator is to determine the Least Common Multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators.
Example:
Compare 1/3 and 1/4.
The denominators are 3 and 4. The LCM of 3 and 4 is 12.
4.2. Converting Fractions to Equivalent Fractions
Once you have the common denominator, convert each fraction into an equivalent fraction with that denominator. To do this, multiply both the numerator and the denominator of each fraction by the number that makes the original denominator equal to the common denominator.
Example (continued):
- To convert 1/3 to a fraction with a denominator of 12, multiply both the numerator and the denominator by 4:
1/3 x 4/4 = 4/12 - To convert 1/4 to a fraction with a denominator of 12, multiply both the numerator and the denominator by 3:
1/4 x 3/3 = 3/12
Now you have two equivalent fractions: 4/12 and 3/12.
4.3. Comparing Fractions with Common Denominators
After converting the fractions to equivalent fractions with a common denominator, you can compare them by looking at their numerators, just as you would with fractions that originally had the same denominator.
Example (continued):
Compare 4/12 and 3/12.
Since both fractions now have the same denominator (12), compare the numerators (4 and 3). Since 4 is greater than 3, 4/12 > 3/12. Therefore, 1/3 > 1/4.
4.4. Step-by-Step Guide to Comparing Fractions with Different Denominators
- Identify the Fractions: Note the fractions you want to compare.
- Find the LCM: Determine the Least Common Multiple (LCM) of the denominators.
- Convert to Equivalent Fractions: Convert each fraction to an equivalent fraction with the LCM as the new denominator.
- Compare the Numerators: Compare the numerators of the equivalent fractions. The fraction with the larger numerator is the larger fraction.
- Conclude: State which of the original fractions is larger based on the comparison of the numerators.
5. Methods for Finding the Least Common Multiple (LCM)
Finding the LCM is a crucial step in comparing fractions with different denominators. There are several methods to find the LCM, each with its own advantages.
5.1. Listing Multiples
One of the simplest methods for finding the LCM is to list the multiples of each denominator until you find a common multiple.
Example:
Find the LCM of 4 and 6.
- Multiples of 4: 4, 8, 12, 16, 20, 24, …
- Multiples of 6: 6, 12, 18, 24, 30, …
The smallest multiple that appears in both lists is 12. Therefore, the LCM of 4 and 6 is 12.
5.2. Prime Factorization
Prime factorization involves breaking down each denominator into its prime factors. The LCM is then found by multiplying the highest power of each prime factor that appears in either factorization.
Example:
Find the LCM of 12 and 18.
- Prime factorization of 12: 2^2 x 3
- Prime factorization of 18: 2 x 3^2
The highest power of 2 is 2^2, and the highest power of 3 is 3^2. Therefore, the LCM is 2^2 x 3^2 = 4 x 9 = 36.
5.3. Using the Greatest Common Divisor (GCD)
The Greatest Common Divisor (GCD) is the largest number that divides both denominators without leaving a remainder. The LCM can be found using the formula:
LCM(a, b) = (a x b) / GCD(a, b)
Example:
Find the LCM of 24 and 36.
- The GCD of 24 and 36 is 12.
- LCM(24, 36) = (24 x 36) / 12 = 864 / 12 = 72
Therefore, the LCM of 24 and 36 is 72.
6. Alternative Methods for Comparing Fractions
While finding a common denominator is a reliable method, there are alternative approaches that can be more efficient in certain situations.
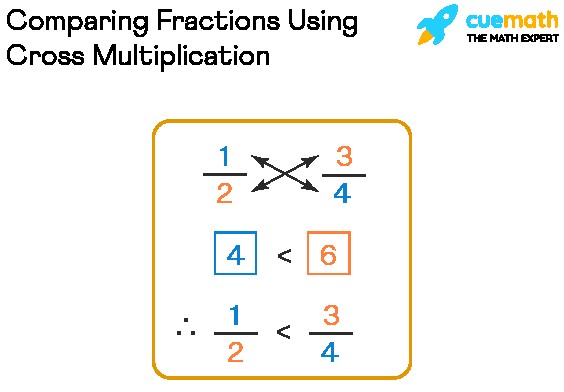
6.1. Cross Multiplication
Cross multiplication is a quick method for comparing two fractions. Multiply the numerator of the first fraction by the denominator of the second fraction, and multiply the numerator of the second fraction by the denominator of the first fraction. Then, compare the results.
Example:
Compare 3/4 and 5/7.
- 3 x 7 = 21
- 5 x 4 = 20
Since 21 is greater than 20, 3/4 > 5/7.
6.2. Converting to Decimals
Converting fractions to decimals involves dividing the numerator by the denominator. Once both fractions are in decimal form, they can be easily compared.
Example:
Compare 3/8 and 5/16.
- 3/8 = 0.375
- 5/16 = 0.3125
Since 0.375 is greater than 0.3125, 3/8 > 5/16.
6.3. Benchmarking
Benchmarking involves comparing fractions to common reference points, such as 0, ½, and 1. This method is particularly useful for quickly estimating the relative size of fractions.
Example:
Compare 2/5 and 5/8.
- 2/5 is less than ½ (which is 2.5/5).
- 5/8 is greater than ½ (which is 4/8).
Therefore, 5/8 > 2/5.
7. Special Cases and Considerations
Certain scenarios require special attention when comparing fractions. Understanding these cases can prevent common mistakes and ensure accurate comparisons.
7.1. Comparing Mixed Numbers
Mixed numbers consist of a whole number and a proper fraction. To compare mixed numbers, first compare the whole numbers. If the whole numbers are different, the mixed number with the larger whole number is the larger mixed number. If the whole numbers are the same, compare the fractional parts.
Example:
Compare 3 1/4 and 2 3/4.
Since 3 is greater than 2, 3 1/4 > 2 3/4.
Example:
Compare 4 2/5 and 4 3/10.
The whole numbers are the same (4). Compare the fractional parts: 2/5 and 3/10.
- Convert 2/5 to an equivalent fraction with a denominator of 10: 2/5 x 2/2 = 4/10.
- Compare 4/10 and 3/10. Since 4 is greater than 3, 4/10 > 3/10.
- Therefore, 4 2/5 > 4 3/10.
7.2. Comparing Negative Fractions
When comparing negative fractions, remember that the fraction closer to zero is larger. To compare negative fractions, first ignore the negative signs and compare the absolute values of the fractions. Then, reverse the comparison.
Example:
Compare -1/3 and -1/4.
- Compare the absolute values: 1/3 and 1/4.
- We know that 1/3 > 1/4.
- Therefore, -1/3 < -1/4.
7.3. Comparing Fractions to Whole Numbers
To compare a fraction to a whole number, convert the whole number into a fraction with the same denominator as the fraction. Then, compare the numerators.
Example:
Compare 3/5 and 1.
- Convert 1 to a fraction with a denominator of 5: 1 = 5/5.
- Compare 3/5 and 5/5. Since 5 is greater than 3, 5/5 > 3/5.
- Therefore, 1 > 3/5.
8. Common Mistakes and How to Avoid Them
Comparing fractions can be challenging, and it’s easy to make mistakes. Here are some common errors and how to avoid them:
8.1. Ignoring the Denominator
A common mistake is to focus solely on the numerator when comparing fractions with different denominators. Always remember to find a common denominator before comparing the numerators.
Example:
Incorrect: 1/3 > 1/2 (because 1 > 1)
Correct: 1/3 = 2/6, 1/2 = 3/6. Therefore, 1/2 > 1/3.
8.2. Incorrectly Finding the LCM
Finding the correct LCM is crucial. Double-check your calculations to ensure you have the smallest common multiple.
Example:
Incorrect LCM of 4 and 6: 24 (instead of 12)
Correct LCM of 4 and 6: 12
8.3. Not Simplifying Fractions
Simplifying fractions before comparing them can make the process easier. Always reduce fractions to their simplest form before finding a common denominator.
Example:
Compare 4/8 and 1/4.
- Simplify 4/8 to 1/2.
- Now compare 1/2 and 1/4.
8.4. Forgetting to Adjust the Numerator
When converting fractions to equivalent fractions, remember to multiply both the numerator and the denominator by the same number.
Example:
Incorrect: 1/3 = 4/3 (only multiplying the numerator by 4)
Correct: 1/3 = 4/12 (multiplying both numerator and denominator by 4)
9. Practice Exercises
To reinforce your understanding of comparing fractions, try these practice exercises:
- Compare 2/5 and 3/7.
- Compare 5/8 and 7/12.
- Compare 1 2/3 and 1 3/5.
- Compare -2/3 and -3/4.
- Compare 4/9 and 1/2.
Answers:
- 3/7 > 2/5
- 5/8 > 7/12
- 1 3/5 > 1 2/3
- -2/3 > -3/4
- 1/2 > 4/9
10. The Role of COMPARE.EDU.VN in Simplifying Fraction Comparisons
At COMPARE.EDU.VN, we understand that comparing fractions can be a daunting task. That’s why we provide resources and tools to simplify the process, making it accessible to everyone.
10.1. Tools and Resources Available
- Fraction Comparison Calculators: Our online calculators allow you to input fractions and instantly see which is larger. These tools are perfect for quick checks and complex comparisons.
- Educational Articles: We offer a wide range of articles explaining the concepts behind fraction comparison, providing step-by-step guides and examples.
- Practice Quizzes: Test your knowledge with our practice quizzes, designed to reinforce your understanding of fraction comparison techniques.
10.2. How COMPARE.EDU.VN Makes Learning Easier
- Step-by-Step Guides: Our guides break down complex concepts into manageable steps, making it easier to understand and apply the techniques.
- Visual Aids: We use visual aids, such as diagrams and charts, to illustrate fraction comparison methods, helping you visualize the concepts.
- Real-World Examples: Our examples are grounded in real-world scenarios, showing you how fraction comparison is used in everyday life.
10.3. Encouraging Users to Explore Further
We encourage you to explore our website, COMPARE.EDU.VN, for more resources and tools to enhance your understanding of fractions and other mathematical concepts. Whether you are a student, a professional, or simply someone looking to improve your math skills, our website has something for you.
11. Conclusion: Mastering Fraction Comparisons
Comparing fractions, especially those with different numerators and denominators, is a critical skill with wide-ranging applications. By understanding the fundamental concepts and utilizing effective methods, you can confidently compare fractions and make informed decisions in various aspects of life.
11.1. Recap of Key Points
- Understanding Fractions: A fraction represents a part of a whole and consists of a numerator and a denominator.
- Common Denominators: To compare fractions with different denominators, find a common denominator (LCM) and convert the fractions to equivalent fractions.
- Alternative Methods: Cross multiplication, converting to decimals, and benchmarking are alternative methods for comparing fractions.
- Special Cases: Pay attention to mixed numbers, negative fractions, and comparing fractions to whole numbers.
- Avoiding Mistakes: Be mindful of common errors, such as ignoring the denominator and incorrectly finding the LCM.
11.2. Encouragement to Practice and Improve
Practice is key to mastering fraction comparisons. The more you practice, the more confident and proficient you will become. Use the practice exercises provided and explore additional resources on COMPARE.EDU.VN to continue improving your skills.
11.3. Final Thoughts on the Importance of Fraction Skills
Fraction skills are not just important for academic success; they are essential for navigating the complexities of everyday life. From cooking and finance to construction and data analysis, the ability to compare fractions empowers you to make informed decisions and solve real-world problems.
12. Frequently Asked Questions (FAQs)
12.1. What is the easiest way to compare fractions with different denominators?
The easiest way is often to use cross multiplication or convert the fractions to decimals. Cross multiplication is quick for comparing two fractions, while converting to decimals allows for easy comparison using decimal values.
12.2. How do I find the Least Common Multiple (LCM)?
You can find the LCM by listing multiples, using prime factorization, or using the Greatest Common Divisor (GCD). Listing multiples involves writing out multiples of each denominator until you find a common one. Prime factorization involves breaking down each number into prime factors and multiplying the highest powers of each. The GCD method uses the formula LCM(a, b) = (a x b) / GCD(a, b).
12.3. What if I’m comparing more than two fractions?
When comparing more than two fractions, find a common denominator for all the fractions. Convert each fraction to an equivalent fraction with the common denominator, and then compare the numerators.
12.4. How do I compare mixed numbers?
First, compare the whole numbers. If they are different, the mixed number with the larger whole number is larger. If the whole numbers are the same, compare the fractional parts.
12.5. What do I do if the fractions are negative?
When comparing negative fractions, compare their absolute values first. Then, reverse the comparison. For example, if 1/3 > 1/4, then -1/3 < -1/4.
12.6. Can I always use cross multiplication?
Cross multiplication is a quick method for comparing two fractions but may not be as efficient when comparing multiple fractions.
12.7. Why is finding a common denominator important?
Finding a common denominator allows you to compare the fractions directly by looking at their numerators, ensuring an accurate comparison.
12.8. Are there any online tools to help compare fractions?
Yes, there are many online tools and calculators that can help you compare fractions quickly and accurately. COMPARE.EDU.VN offers such tools to simplify the process.
12.9. What is benchmarking in fraction comparison?
Benchmarking involves comparing fractions to common reference points like 0, ½, and 1. This method is useful for quickly estimating the relative size of fractions.
12.10. How can I practice comparing fractions?
Practice by working through examples, using online quizzes, and applying fraction comparison in real-world scenarios like cooking and finance.
By mastering these techniques and avoiding common mistakes, you can confidently compare fractions and enhance your mathematical skills. Remember to visit COMPARE.EDU.VN for more resources and tools to help you on your learning journey.
For further assistance, please visit our website at compare.edu.vn, or contact us at 333 Comparison Plaza, Choice City, CA 90210, United States, or via WhatsApp at +1 (626) 555-9090. We are here to help you make informed decisions and achieve your goals.