How Do You Compare Decimals? A Comprehensive Guide

Comparing decimals can seem tricky, but it’s a fundamental skill with applications in everyday life. At COMPARE.EDU.VN, we break down the process into easy-to-understand steps. This guide provides a comprehensive overview of decimal comparison, ensuring you can confidently determine which decimal is larger or smaller. Understanding the concepts and comparing different decimal numbers will be easy with our guide.

1. What Is Comparing Decimals?

Comparing decimals involves determining which decimal number has a greater or lesser value when you have a set of numbers. This is similar to comparing whole numbers, but with the added consideration of the digits after the decimal point. The position of each number after the decimal point is essential since it determines place value.

To compare decimals, begin by comparing the digits in the largest place value position. If they are equal, move to the next place value to the right until you find digits that differ. The decimal with the larger digit in that place value is the larger number. This method ensures an accurate and efficient comparison of decimal numbers.

Example: Compare 12.45 and 12.62

Both numbers have the same whole number part (12).
Compare the tenths place: 4 vs. 6.
Since 6 is greater than 4, 12.62 is greater than 12.45.

This simple process can be applied to any set of decimals, making it a valuable skill for various applications.

2. Understanding Decimal Place Value

To effectively compare decimals, it’s crucial to understand place value. Each digit in a decimal number holds a specific value based on its position relative to the decimal point.

The digit immediately to the left of the decimal point represents the ones place.
Moving left from the ones place, you have tens, hundreds, thousands, and so on.
The digit immediately to the right of the decimal point represents the tenths place (1/10).
The next digit to the right is the hundredths place (1/100), followed by the thousandths place (1/1000), and so on.

Understanding this structure allows you to accurately compare digits in corresponding place values.

For example, in the number 3.145:

3 is in the ones place.
1 is in the tenths place.
4 is in the hundredths place.
5 is in the thousandths place.

Knowing these place values makes comparing decimals much easier, as you can directly compare the values in each position.

3. Step-by-Step Guide to Comparing Decimals

Here’s a detailed guide on how to compare decimal numbers effectively:

Align the Decimal Points: Write the numbers vertically, aligning the decimal points. This ensures that you are comparing digits in the same place value.
Add Trailing Zeros (if needed): If the numbers have different numbers of digits after the decimal point, add trailing zeros to the shorter number so that both numbers have the same number of decimal places. This does not change the value of the number but makes it easier to compare.
Compare the Whole Number Part: Start by comparing the digits to the left of the decimal point. If one number has a larger whole number part, that number is larger.
Compare the Tenths Place: If the whole number parts are equal, move to the tenths place (the first digit to the right of the decimal point). The number with the larger digit in the tenths place is larger.
Continue Comparing Place Values: If the tenths digits are equal, continue moving to the right, comparing the hundredths place, thousandths place, and so on, until you find digits that are different.
Determine the Larger Number: Once you find a place value where the digits differ, the number with the larger digit in that place value is the larger number.

Example: Compare 4.25 and 4.235

Align the decimal points:
```
4.25
4.235
```
Add trailing zeros to 4.25:
```
4.250
4.235
```
Compare the whole number part: Both are 4.
Compare the tenths place: Both are 2.
Compare the hundredths place: 5 vs. 3.
Since 5 is greater than 3, 4.25 is greater than 4.235.

4. Comparing Decimals and Fractions

Sometimes, you need to compare a decimal to a fraction. To do this, convert the fraction to a decimal, and then compare the two decimals using the steps outlined above. Converting fractions to decimals involves dividing the numerator by the denominator.

Example: Compare 0.65 and 3/5

Convert the fraction 3/5 to a decimal: 3 ÷ 5 = 0.6
Now compare 0.65 and 0.6
Add a trailing zero to 0.6: 0.60
Compare the tenths place: Both are 6.
Compare the hundredths place: 5 vs. 0.
Since 5 is greater than 0, 0.65 is greater than 3/5.

Converting fractions to decimals simplifies the comparison process, making it easier to determine which value is larger.

5. Using a Number Line to Compare Decimals

A number line is a visual tool that can help you compare decimals. Draw a number line and plot the decimals you want to compare. The number that lies further to the right on the number line is the larger number.

Example: Compare 2.3 and 2.7 on a number line.

Draw a number line that includes the range from 2 to 3.
Mark 2.3 and 2.7 on the number line.
Since 2.7 is to the right of 2.3, 2.7 is greater than 2.3.

Using a number line provides a clear visual representation, especially useful for those who prefer visual learning methods.

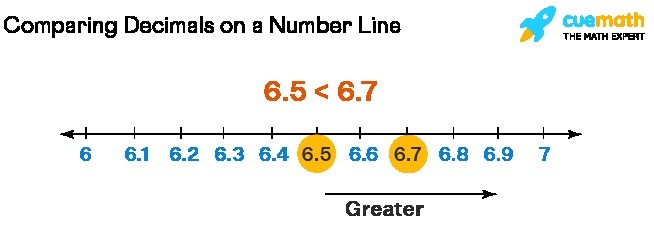Comparing Decimals on a Number Line

Alt Text: Number line showing the comparison of decimals 2.3 and 2.7, with 2.7 being to the right and thus larger.

6. Common Mistakes to Avoid When Comparing Decimals

Avoiding common mistakes ensures accurate decimal comparisons. Here are a few pitfalls to watch out for:

Ignoring Place Value: Failing to consider the place value of digits can lead to incorrect comparisons. For example, thinking that 0.9 is less than 0.12 because 9 is less than 12.
Not Aligning Decimal Points: Misaligning decimal points when comparing vertically can cause you to compare digits in different place values.
Incorrectly Converting Fractions: Making errors when converting fractions to decimals can lead to wrong comparisons. Always double-check your division.
Forgetting Trailing Zeros: Not adding trailing zeros when necessary can result in misinterpreting the value of decimals.
Rushing the Process: Taking shortcuts and not carefully comparing each digit can lead to mistakes.

By being aware of these common errors, you can take steps to avoid them and ensure accurate comparisons.

7. Real-World Applications of Comparing Decimals

Comparing decimals is not just a mathematical exercise; it has practical applications in various real-world scenarios.

Shopping: Comparing prices per unit to find the best deal. For example, comparing the price of two different sizes of the same product to determine which offers better value.
Cooking: Adjusting recipes based on decimal measurements. For example, scaling a recipe that calls for 0.75 cups of flour.
Finance: Comparing interest rates or investment returns. For example, choosing between two savings accounts with interest rates of 2.5% and 2.75%.
Sports: Comparing statistics such as batting averages or race times. For example, determining which baseball player has a higher batting average based on decimals.
Science: Analyzing data in experiments that involve decimal measurements. For example, comparing the results of two experiments with measurements like 3.25 grams and 3.27 grams.

These examples illustrate how comparing decimals is a valuable skill in everyday life, helping you make informed decisions and solve practical problems.

8. Advanced Techniques for Comparing Decimals

While the basic method of comparing decimals works well for most situations, there are some advanced techniques that can be helpful in more complex scenarios:

Using Benchmarks: Compare decimals to common benchmarks like 0.25 (1/4), 0.5 (1/2), and 0.75 (3/4). This can help you quickly estimate the relative size of decimals.
Converting to Percentages: Convert decimals to percentages by multiplying by 100. Comparing percentages can sometimes be easier than comparing decimals directly.
Scientific Notation: For very large or very small decimals, using scientific notation can simplify the comparison process.
Approximation: Rounding decimals to the nearest tenth or hundredth can make them easier to compare, especially when dealing with long decimals.
Estimation: Estimating the value of decimals can help you quickly determine which is larger without needing to compare every digit.

These advanced techniques provide additional tools for comparing decimals efficiently and accurately, particularly in more challenging situations.

9. How Decimal Place Value Impacts Comparison

Understanding decimal place value is crucial for accurately comparing decimals. The value of each digit depends on its position relative to the decimal point. Here’s how place value impacts the comparison:

Tenths Place: The digit immediately to the right of the decimal point represents tenths (1/10). Comparing the tenths place is often the first step in determining which decimal is larger.
Hundredths Place: The second digit to the right of the decimal point represents hundredths (1/100). If the tenths places are equal, comparing the hundredths place becomes important.
Thousandths Place: The third digit to the right of the decimal point represents thousandths (1/1000). This place value is considered when the tenths and hundredths places are equal.
Higher Place Values: As you move further to the right, each subsequent digit represents a smaller fraction (ten-thousandths, hundred-thousandths, etc.). These higher place values are considered only when all previous digits are equal.

By understanding how each digit contributes to the overall value of the decimal, you can make more accurate comparisons.

Example: Compare 0.456 and 0.459

Tenths place: Both are 4 (0.4).
Hundredths place: Both are 5 (0.05).
Thousandths place: 6 vs. 9 (0.006 vs. 0.009).
Since 9 is greater than 6, 0.459 is greater than 0.456.

10. Practice Exercises for Mastering Decimal Comparison

Practice is essential for mastering any skill, and comparing decimals is no exception. Here are some exercises to help you improve your decimal comparison abilities:

Basic Comparison:
- Compare 3.25 and 3.27
- Compare 0.5 and 0.48
- Compare 1.75 and 1.8
Fraction Comparison:
- Compare 0.75 and 4/5
- Compare 0.2 and 1/6
- Compare 0.6 and 2/3
Number Line Comparison:
- Plot 2.1 and 2.4 on a number line and compare.
- Plot 0.8 and 0.95 on a number line and compare.
Real-World Problems:
- A store sells apples for $1.25 each and oranges for $1.30 each. Which is cheaper?
- A runner completes a race in 12.5 seconds, and another completes it in 12.45 seconds. Who is faster?
Advanced Comparison:
- Compare 0.0056 and 0.0052
- Compare 1.4567 and 1.457

By working through these exercises, you’ll reinforce your understanding of decimal comparison and build confidence in your abilities.

11. Using Tools and Resources for Decimal Comparison

Several tools and resources can help you compare decimals more efficiently and accurately. These include:

Calculators: Calculators can quickly convert fractions to decimals and compare decimal values.
Online Decimal Comparators: Many websites offer online tools that allow you to enter two or more decimals and instantly determine which is larger.
Educational Websites: Websites like COMPARE.EDU.VN provide lessons, examples, and practice exercises to help you learn and improve your decimal comparison skills.
Mobile Apps: Numerous mobile apps are designed to help with math skills, including decimal comparison.
Textbooks and Workbooks: Math textbooks and workbooks often include sections on decimal comparison with detailed explanations and practice problems.

These tools and resources can supplement your learning and provide additional support as you master decimal comparison.

12. Common Scenarios Where Decimal Comparison Is Useful

Understanding how to compare decimals is practical in various everyday situations. Here are a few scenarios where this skill comes in handy:

Grocery Shopping: Comparing the price per unit of different products to find the best value. For example, deciding between two brands of cereal based on their price per ounce.
Fuel Efficiency: Comparing the gas mileage of different vehicles to determine which is more fuel-efficient. For example, choosing between a car that gets 32.5 miles per gallon and one that gets 33.2 miles per gallon.
Interest Rates: Comparing interest rates on loans or savings accounts to make informed financial decisions. For example, selecting a credit card with a lower interest rate of 15.75% compared to one with 16.25%.
Measurement Conversion: Converting measurements from one unit to another and comparing the results. For example, converting inches to centimeters and comparing the lengths of two objects.
Sports Statistics: Analyzing sports statistics to compare the performance of athletes or teams. For example, comparing batting averages in baseball to determine which player is more consistent.

13. Tips for Teaching Decimal Comparison to Others

If you’re helping someone else learn how to compare decimals, here are some tips to make the process easier:

Start with the Basics: Ensure they have a solid understanding of place value and decimal notation before moving on to comparison.
Use Visual Aids: Number lines, charts, and diagrams can help visualize the comparison process.
Provide Real-World Examples: Relate the concept to everyday situations, such as shopping or cooking, to make it more relevant.
Break It Down: Break the comparison process into simple, step-by-step instructions.
Encourage Practice: Provide plenty of opportunities for practice with a variety of exercises.
Address Common Mistakes: Be aware of common mistakes and address them proactively.
Be Patient: Learning takes time, so be patient and supportive.
Use Manipulatives: Tools like base-ten blocks can visually represent decimals and aid in understanding.

By following these tips, you can effectively teach others how to compare decimals and build their confidence in math.

14. Why Decimal Comparison Is a Foundational Math Skill

Decimal comparison is more than just a math exercise; it’s a foundational skill that supports many other mathematical concepts. Here’s why it’s important:

Understanding Number Systems: Comparing decimals reinforces an understanding of the number system and how values relate to each other.
Problem-Solving: It builds problem-solving skills that are applicable in various contexts.
Critical Thinking: It encourages critical thinking as you analyze and compare different values.
Preparation for Advanced Math: It lays the groundwork for more advanced math topics, such as algebra and calculus.
Real-World Applications: It has numerous real-world applications, making it a valuable skill for everyday life.

Mastering decimal comparison can significantly improve your overall math proficiency and prepare you for future learning.

15. The Importance of Accuracy in Decimal Comparison

Accuracy is crucial when comparing decimals, as even small errors can lead to incorrect decisions. Here’s why accuracy matters:

Financial Decisions: Inaccurate comparisons can lead to poor financial decisions, such as choosing a loan with a higher interest rate.
Scientific Experiments: In scientific experiments, inaccurate measurements can lead to incorrect conclusions.
Engineering Projects: In engineering projects, precise measurements are essential for ensuring safety and functionality.
Medical Dosages: Inaccurate decimal comparisons can lead to incorrect medication dosages, which can have serious consequences.
Construction: In construction, inaccurate measurements can result in structural problems.

Taking the time to carefully compare decimals and double-check your work can help you avoid costly errors and make better decisions in various aspects of life.

16. Strategies for Simplifying Complex Decimal Comparisons

When faced with complex decimal comparisons, using simplifying strategies can make the process easier and more manageable. Here are some effective techniques:

Break It Down: Divide the comparison into smaller, more manageable steps.
Use Benchmarks: Compare decimals to common benchmarks like 0.25, 0.5, and 0.75 to get a general sense of their relative size.
Rounding: Round decimals to the nearest tenth or hundredth to make them easier to compare.
Estimation: Estimate the value of decimals to quickly determine which is larger without needing to compare every digit.
Visual Aids: Use number lines or charts to visualize the comparison process.
Technology: Utilize calculators and online tools to assist with complex calculations.
Recheck: Always double-check your work to ensure accuracy.

By applying these strategies, you can simplify even the most complex decimal comparisons and arrive at the correct answer more efficiently.

17. Exploring Different Methods of Visualizing Decimal Values

Visualizing decimal values can enhance understanding and make comparisons easier. Here are some effective methods:

Number Lines: Plot decimals on a number line to see their relative positions.
Charts and Tables: Create charts or tables that show the place value of each digit in a decimal.
Base-Ten Blocks: Use base-ten blocks to represent decimals visually.
Graphs: Use graphs to plot decimal values and compare them.
Diagrams: Draw diagrams that represent decimals as parts of a whole.
Interactive Tools: Use interactive online tools that allow you to manipulate decimals and see their values change.

These visualization methods can help make the abstract concept of decimals more concrete and accessible, leading to a better understanding of decimal comparison.

18. How Does Decimal Comparison Relate To Percentages

Decimal comparison is closely related to percentages, as percentages are simply decimals multiplied by 100. Understanding this relationship can make it easier to compare values in different formats.

Converting Decimals to Percentages: To convert a decimal to a percentage, multiply it by 100. For example, 0.75 = 75%.
Converting Percentages to Decimals: To convert a percentage to a decimal, divide it by 100. For example, 60% = 0.6.
Comparing Decimals and Percentages: When comparing a decimal and a percentage, convert both values to the same format (either both decimals or both percentages) before comparing.
Real-World Applications: Percentages are often used in real-world scenarios, such as calculating discounts or interest rates. Understanding how to convert between decimals and percentages can help you make informed decisions.

By understanding the relationship between decimals and percentages, you can easily switch between the two formats and compare values more effectively.

19. Mastering Decimal Comparison for Academic Success

Mastering decimal comparison is essential for academic success in mathematics and related subjects. Here’s how it supports learning:

Foundational Skill: It’s a foundational skill that underlies many other mathematical concepts.
Problem-Solving: It builds problem-solving skills that are applicable in various contexts.
Critical Thinking: It encourages critical thinking as you analyze and compare different values.
Preparation for Advanced Math: It lays the groundwork for more advanced math topics, such as algebra and calculus.
Test Performance: Proficiency in decimal comparison can improve your performance on math tests and assessments.

By mastering decimal comparison, you can build a strong foundation in mathematics and improve your academic performance.

20. Overcoming Challenges in Decimal Comparison

Even with a solid understanding of the basics, you may encounter challenges when comparing decimals. Here are some common challenges and strategies for overcoming them:

Long Decimals: When comparing long decimals, focus on the digits in the leftmost place value where they differ.
Decimals with Many Zeros: Be careful when comparing decimals with many zeros, as it’s easy to make mistakes. Align the decimal points and compare each digit carefully.
Negative Decimals: Remember that negative decimals are smaller than positive decimals. When comparing two negative decimals, the one with the larger absolute value is smaller.
Fractions and Decimals: Convert fractions to decimals before comparing them to decimals.
Complex Comparisons: Break complex comparisons into smaller, more manageable steps.

By being aware of these challenges and using the appropriate strategies, you can overcome them and accurately compare decimals in any situation.

21. Decimal Comparison in Everyday Finance

Decimal comparison is a crucial skill in everyday finance, helping you make informed decisions about spending, saving, and investing. Here are some examples:

Comparing Prices: When shopping, compare the prices of different items to find the best deal. For example, deciding between two brands of peanut butter based on their price per ounce.
Calculating Discounts: Calculate discounts by converting percentages to decimals and multiplying them by the original price. For example, calculating the sale price of an item that is 20% off.
Comparing Interest Rates: Compare interest rates on loans or savings accounts to make informed financial decisions. For example, selecting a credit card with a lower interest rate.
Budgeting: Create a budget by tracking your income and expenses in decimal format. For example, allocating a certain percentage of your income to rent, food, and entertainment.
Investing: Compare the returns on different investments to make informed investment decisions. For example, choosing between two stocks based on their potential returns.

By mastering decimal comparison, you can take control of your finances and make smarter decisions about your money.

22. How to Explain Decimal Comparison to Children

Explaining decimal comparison to children can be made easier by using relatable examples and visual aids. Here are some tips:

Start with Real-World Examples: Use examples that children can relate to, such as comparing the heights of friends or the prices of toys.
Use Visual Aids: Use number lines, charts, and diagrams to help visualize the comparison process.
Relate to Fractions: Explain that decimals are just another way to represent fractions, and that comparing decimals is like comparing fractions with a denominator of 10, 100, or 1000.
Use Manipulatives: Use tools like base-ten blocks or money to visually represent decimals and aid in understanding.
Break It Down: Break the comparison process into simple, step-by-step instructions.
Encourage Questions: Encourage children to ask questions and provide clear, simple answers.
Make It Fun: Turn the learning process into a game by using fun activities and rewards.

By following these tips, you can effectively explain decimal comparison to children and help them develop a strong foundation in math.

23. Tips for Memorizing Decimal Place Values

Memorizing decimal place values is essential for accurately comparing decimals. Here are some tips to help you remember them:

Use Flashcards: Create flashcards with the place values on one side and their corresponding values on the other side.
Practice Regularly: Practice identifying the place values of digits in decimals regularly.
Use Mnemonics: Create mnemonics or memory aids to help you remember the order of the place values.
Relate to Fractions: Remember that each place value corresponds to a fraction with a denominator of 10, 100, 1000, and so on.
Use Visual Aids: Use charts or diagrams that show the place values of digits in decimals.
Teach Others: Teaching others about decimal place values can help reinforce your own understanding.

By following these tips, you can effectively memorize decimal place values and improve your accuracy when comparing decimals.

24. Fun Activities to Practice Decimal Comparison

Making learning fun can greatly enhance understanding and retention. Here are some fun activities to practice decimal comparison:

Decimal War: Play a card game where each player draws two cards and forms a decimal. The player with the larger decimal wins the round.
Decimal Bingo: Create bingo cards with decimals and call out other decimals. Players mark off the corresponding decimals on their cards.
Decimal Scavenger Hunt: Hide decimals around the room and have players find them and arrange them in order from least to greatest.
Decimal Dice Game: Roll dice to create decimals and have players compare them.
Decimal Board Game: Create a board game where players move along a path and compare decimals to advance.

By incorporating these fun activities into your learning routine, you can make practicing decimal comparison more enjoyable and effective.

25. Decimal Comparison and Scientific Notation

Decimal comparison is also essential when working with scientific notation, a way to express very large or very small numbers in a more manageable format. Scientific notation involves writing a number as a decimal between 1 and 10 multiplied by a power of 10.

Converting to Scientific Notation: To convert a decimal to scientific notation, move the decimal point until there is only one non-zero digit to the left of the decimal point. The number of places you moved the decimal point determines the exponent of 10.
Comparing Numbers in Scientific Notation: To compare numbers in scientific notation, first compare the exponents of 10. The number with the larger exponent is larger. If the exponents are equal, compare the decimal parts.
Examples:
- Compare 3.2 x 10^5 and 2.8 x 10^6. Since 10^6 is larger than 10^5, 2.8 x 10^6 is larger.
- Compare 4.5 x 10^-3 and 5.2 x 10^-3. Since the exponents are equal, compare the decimal parts. 5.2 is larger than 4.5, so 5.2 x 10^-3 is larger.

Understanding how to compare numbers in scientific notation can be useful in various scientific and mathematical contexts.

26. Using Technology to Enhance Decimal Comparison Skills

Technology offers numerous tools and resources that can enhance your decimal comparison skills. Here are some examples:

Online Calculators: Use online calculators to quickly convert fractions to decimals and compare decimal values.
Educational Websites: Explore educational websites like COMPARE.EDU.VN that offer lessons, examples, and practice exercises to help you learn and improve your decimal comparison skills.
Mobile Apps: Download mobile apps designed to help with math skills, including decimal comparison.
Interactive Tools: Use interactive online tools that allow you to manipulate decimals and see their values change.
Video Tutorials: Watch video tutorials that explain decimal comparison in a clear and concise manner.

By leveraging technology, you can access a wide range of resources that can support your learning and help you master decimal comparison.

27. Why Consistent Practice Is Essential for Decimal Comparison Mastery

Consistent practice is essential for mastering any skill, and decimal comparison is no exception. Here’s why regular practice matters:

Reinforcement: Practice reinforces your understanding of the concepts and helps you remember them.
Skill Development: Practice helps you develop your skills and improve your accuracy and speed.
Confidence Building: Practice builds your confidence and makes you more comfortable with the material.
Retention: Regular practice helps you retain what you’ve learned over time.
Problem-Solving: Practice provides opportunities to apply your skills to solve problems and develop your problem-solving abilities.

By making decimal comparison practice a regular part of your learning routine, you can achieve mastery and build a strong foundation in math.

28. Understanding Decimal Comparison and Significant Figures

When comparing decimals, it’s important to consider significant figures, which are the digits in a number that carry meaningful information about its precision. Here’s how significant figures relate to decimal comparison:

Identifying Significant Figures: Significant figures include all non-zero digits, zeros between non-zero digits, and trailing zeros in a number with a decimal point.
Comparing Numbers with Different Significant Figures: When comparing numbers with different significant figures, the number with more significant figures is generally considered more precise.
Rounding: When performing calculations with decimals, it’s important to round your answer to the correct number of significant figures.
Examples:
- The number 3.14 has three significant figures.
- The number 0.0056 has two significant figures.
- The number 2.050 has four significant figures.

Understanding significant figures can help you make more accurate and informed comparisons of decimals.

29. Exploring the History and Evolution of Decimal Numbers

Understanding the history and evolution of decimal numbers can provide valuable context and appreciation for this important mathematical concept. Here are some key milestones:

Ancient Civilizations: Ancient civilizations, such as the Egyptians and Babylonians, used fractional numbers but did not have a standardized system for representing them.
The Development of Decimal Notation: The development of decimal notation is attributed to various mathematicians, including Simon Stevin in the 16th century.
The Spread of Decimal Numbers: Decimal numbers gradually spread throughout Europe and the rest of the world, becoming an essential tool for science, engineering, and commerce.
Modern Use of Decimal Numbers: Today, decimal numbers are used in countless applications, from measuring distances to calculating financial transactions.

By exploring the history and evolution of decimal numbers, you can gain a deeper understanding of their significance and importance.

30. Mastering Decimal Comparison for Career Advancement

Mastering decimal comparison can be a valuable asset for career advancement in various fields. Here are some examples:

Finance: Financial analysts, accountants, and other finance professionals use decimal comparison to make informed decisions about investments, loans, and budgets.
Science and Engineering: Scientists and engineers use decimal comparison to analyze data, conduct experiments, and design projects.
Healthcare: Healthcare professionals use decimal comparison to calculate medication dosages, monitor patient vital signs, and track treatment outcomes.
Business and Marketing: Business professionals and marketers use decimal comparison to analyze sales data, track customer behavior, and measure the effectiveness of marketing campaigns.
Education: Educators use decimal comparison to assess student performance and track academic progress.

By developing your decimal comparison skills, you can enhance your career prospects and increase your earning potential.

Don’t let decimal comparisons intimidate you. With COMPARE.EDU.VN, you have access to the tools and resources needed to master this essential skill. Whether you’re a student, professional, or anyone in between, our comprehensive guide will empower you to confidently compare decimals and make informed decisions.
For more detailed comparisons and decision-making tools, visit compare.edu.vn today. Our experts are here to help you navigate the complexities of choices with clarity and confidence. Contact us at 333 Comparison Plaza, Choice City, CA 90210, United States, or reach out via WhatsApp at +1 (626) 555-9090. We’re here to make comparisons easy.

FAQs About Comparing Decimals

How Do You Compare Decimals With Different Numbers Of Digits?

To compare decimals with different numbers of digits, add trailing zeros to the shorter decimal so that both decimals have the same number of digits after the decimal point. Then, compare the decimals as you would whole numbers. This ensures an accurate comparison by aligning place values. For example, to compare 0.25 and 0.3, rewrite 0.3 as 0.30, then compare 0.25 and 0.30.

What Are Some Common Strategies For Avoiding Mistakes When Comparing Decimals?

Some strategies include aligning the decimal points vertically, adding trailing zeros, comparing digits from left to right, and using a number line for visualization. These techniques minimize errors by ensuring that you compare digits in the same place value and have a clear visual representation of the decimals.

Can You Compare Decimals Without Converting Them To Fractions?

Yes, you can compare decimals directly by aligning the decimal points and comparing digits from left to right. If necessary, add trailing zeros to make the number of decimal places equal. This method allows for a direct comparison without the need for conversion, saving time and effort.

How Do You Compare Negative Decimals?

To compare negative decimals, remember that the number closer to zero is larger. For example, -0.25 is larger than -0.5 because -0.25 is closer to zero on the number line. The absolute value of the decimals can help visualize their distance from zero.

What Should I Do If The Whole Number Parts Of The Decimals Are Different?

If the whole number parts of the decimals are different, simply compare the whole numbers. The decimal with the larger whole number is the larger decimal, regardless of the decimal portion. For example, 5.25 is larger than 4.75 because 5 is greater than 4.

How Does Rounding Affect Decimal Comparison?

Rounding can affect decimal comparison by simplifying the numbers, but it can also introduce inaccuracies. If you round too much, you may lose the ability to accurately compare the decimals. Rounding to the nearest tenth or hundredth is often sufficient for most comparisons while maintaining accuracy.

Is It Possible To Use Estimation For Comparing Decimals?

Yes, estimation can be used for comparing decimals by rounding them to the nearest whole number or tenth and then comparing the rounded values. This method is useful for quickly determining which decimal is larger without needing to compare every digit, though it may not be suitable for precise comparisons.

What Are The Benefits Of Using A Number Line For Decimal Comparison?

Using a number line provides a visual representation of the decimals, making it easier to see their relative positions and determine which is larger. It is particularly helpful for those who are visual learners and for understanding the concept of decimals and their values.

How Do You Compare Repeating Decimals?

To compare repeating decimals, write out enough digits of the repeating part to see a difference, then compare the digits as usual. For example, to compare 0.333… and 0.334, write out 0.333 and 0.334. Clearly, 0.334 is larger than 0.333….

Can I Use A Calculator To Compare Decimals?

Yes, a calculator can be used to compare decimals by simply entering the numbers and comparing the results. Calculators are particularly useful for complex decimals or when converting fractions to decimals for comparison. However, it’s still important to understand the underlying concepts to ensure the calculator is used correctly.