Comparing and ordering decimals can be straightforward when you understand the underlying principles. COMPARE.EDU.VN offers a comprehensive guide to help you master this essential math skill, providing clarity and confidence. Discover the secrets to decimal comparison and sequence, ensuring you’re well-equipped to tackle any numerical challenge with our valuable resources for decimal sorting and ranking.
1. Understanding Decimals and Place Value
Before diving into comparing and ordering decimals, it’s crucial to have a solid understanding of what decimals are and how place value works. Decimals are numbers that include a whole number part and a fractional part, separated by a decimal point. The position of each digit relative to the decimal point determines its value.
1.1 What are Decimals?
Decimals are a way of representing numbers that are not whole. They consist of a whole number part, a decimal point, and a fractional part. For example, in the number 3.14, “3” is the whole number part, and “14” represents the fractional part. This fractional part signifies a value less than one, broken down into tenths, hundredths, thousandths, and so on.
1.2 Place Value Chart
The place value chart is an essential tool for understanding the value of each digit in a decimal number. To the left of the decimal point, you have the ones, tens, hundreds, and so on, just like in whole numbers. To the right of the decimal point, you have tenths, hundredths, thousandths, and so on. Here’s a simplified place value chart:
| Place Value | Value | Example |
|---|---|---|
| Hundreds | 100 | 300 |
| Tens | 10 | 40 |
| Ones | 1 | 5 |
| Decimal Point | . | . |
| Tenths | 1/10 = 0.1 | 0.6 |
| Hundredths | 1/100 = 0.01 | 0.07 |
| Thousandths | 1/1000 = 0.001 | 0.008 |

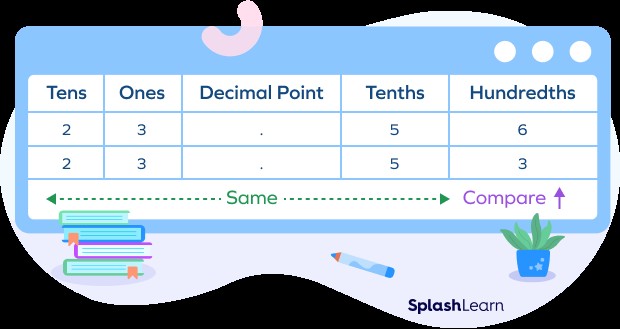
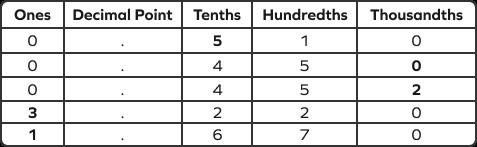
1.3 Why Place Value Matters
Understanding place value is crucial because it allows you to compare and order decimals accurately. The position of a digit determines its contribution to the overall value of the number. For instance, 0.3 is greater than 0.03 because the 3 is in the tenths place in the first number and the hundredths place in the second.
2. Comparing Decimals: Step-by-Step Guide
Comparing decimals involves determining which of two or more decimal numbers is greater or smaller. Here’s a step-by-step guide to help you through the process.
2.1 Align the Decimal Points
The first step in comparing decimals is to align the decimal points vertically. This ensures that you are comparing digits in the same place value.
For example, if you want to compare 4.25 and 4.3, write them like this:
4.25
4.30Notice that we added a zero to 4.3 to make it 4.30. Adding zeros to the right of the last digit after the decimal point does not change the value of the number.
2.2 Compare the Whole Number Part
Start by comparing the whole number part of the decimals. If the whole numbers are different, the decimal with the larger whole number is greater.
Example:
Compare 5.67 and 4.89.
5 > 4, so 5.67 > 4.89.
2.3 Compare the Tenths Place
If the whole numbers are the same, move to the tenths place (the first digit after the decimal point) and compare those digits. The decimal with the larger digit in the tenths place is greater.
Example:
Compare 2.5 and 2.4.
The whole number part is the same (2).
Comparing the tenths place, 5 > 4, so 2.5 > 2.4.
2.4 Compare the Hundredths Place (and Beyond)
If the tenths digits are also the same, continue moving to the right, comparing the hundredths place, thousandths place, and so on, until you find a difference.
Example:
Compare 3.145 and 3.141.
The whole number part is the same (3).
The tenths place is the same (1).
The hundredths place is the same (4).
Comparing the thousandths place, 5 > 1, so 3.145 > 3.141.
2.5 Adding Zeros as Placeholders
Sometimes, one decimal has fewer digits after the decimal point than the other. In such cases, you can add zeros to the right of the shorter decimal to make the comparison easier. Adding zeros does not change the value of the decimal but ensures that you are comparing digits in the same place value.
Example:
Compare 7.8 and 7.85.
Add a zero to 7.8 to make it 7.80.
Now compare 7.80 and 7.85.
The whole number part is the same (7).
The tenths place is the same (8).
Comparing the hundredths place, 0 < 5, so 7.85 > 7.8.
2.6 Using Number Lines
Another helpful method for comparing decimals is to use a number line. Place the decimals on the number line and see which one is further to the right. The decimal further to the right is the larger number.
Example:
Compare 0.6 and 0.8 using a number line.
On a number line from 0 to 1, 0.8 is to the right of 0.6, so 0.8 > 0.6.
3. Ordering Decimals: Ascending and Descending
Ordering decimals means arranging a set of decimal numbers in a specific sequence, either from smallest to largest (ascending order) or from largest to smallest (descending order).
3.1 Ascending Order
Ascending order means arranging the decimals from the smallest to the largest. Follow these steps to order decimals in ascending order:
- Compare the Decimals: Use the steps outlined in Section 2 to compare the decimals pairwise.
- Arrange from Smallest to Largest: Once you have compared the decimals, arrange them in increasing order.
Example:
Order the following decimals in ascending order: 2.35, 2.1, 2.55, 2.05.
- Compare 2.35 and 2.1: 2.1 < 2.35
- Compare 2.35 and 2.55: 2.35 < 2.55
- Compare 2.35 and 2.05: 2.05 < 2.35
Combining these comparisons, the ascending order is: 2.05, 2.1, 2.35, 2.55.
3.2 Descending Order
Descending order means arranging the decimals from the largest to the smallest. Follow these steps to order decimals in descending order:
- Compare the Decimals: Use the steps outlined in Section 2 to compare the decimals pairwise.
- Arrange from Largest to Smallest: Once you have compared the decimals, arrange them in decreasing order.
Example:
Order the following decimals in descending order: 1.75, 1.9, 1.65, 1.8.
- Compare 1.75 and 1.9: 1.9 > 1.75
- Compare 1.75 and 1.65: 1.75 > 1.65
- Compare 1.75 and 1.8: 1.8 > 1.75
Combining these comparisons, the descending order is: 1.9, 1.8, 1.75, 1.65.
4. Real-World Applications of Comparing and Ordering Decimals
Comparing and ordering decimals is not just an academic exercise; it has numerous real-world applications that you encounter in everyday life.
4.1 Shopping and Finance
When shopping, you often need to compare prices to determine which product is the best deal. Prices are usually given in decimal form, so understanding how to compare decimals is essential.
Example:
You are comparing the prices of two similar items:
- Item A: $12.75
- Item B: $12.80
To find the cheaper item, compare the decimals: 12.75 < 12.80, so Item A is cheaper.
In finance, comparing interest rates, investment returns, and loan amounts often involves decimals. Being able to compare these values accurately helps you make informed financial decisions.
4.2 Cooking and Baking
Recipes often require precise measurements, which are frequently given in decimal form. Comparing and ordering these measurements ensures that you use the correct amounts of ingredients.
Example:
A recipe calls for:
- 1.25 cups of flour
- 1.5 cups of sugar
- 1.125 cups of milk
To ensure you add the ingredients in the right proportion, you need to compare the decimal amounts: 1.125 < 1.25 < 1.5.
4.3 Sports and Performance Metrics
In sports, athletes’ performances are often measured using decimals. Comparing these decimals helps determine rankings, records, and improvements.
Example:
In a race, the times of three athletes are:
- Athlete 1: 10.23 seconds
- Athlete 2: 10.15 seconds
- Athlete 3: 10.2 seconds
To determine the winner, compare the decimals: 10.15 < 10.2 < 10.23, so Athlete 2 won the race.
4.4 Science and Engineering
In scientific experiments and engineering projects, precise measurements are critical. These measurements are often in decimal form, and comparing them ensures accuracy and reliability.
Example:
In an experiment, the readings from three sensors are:
- Sensor A: 2.567 volts
- Sensor B: 2.56 volts
- Sensor C: 2.57 volts
To analyze the data, compare the decimals: 2.56 < 2.567 < 2.57.
5. Tips and Tricks for Mastering Decimal Comparison
Here are some additional tips and tricks to help you master the comparison and ordering of decimals:
5.1 Practice Regularly
The more you practice, the more comfortable you will become with comparing and ordering decimals. Use worksheets, online quizzes, and real-life scenarios to reinforce your skills.
5.2 Use Visual Aids
Visual aids like number lines and place value charts can make it easier to understand and compare decimals. These tools help you visualize the value of each digit and make accurate comparisons.
5.3 Break Down Complex Problems
When dealing with complex problems involving multiple decimals, break them down into smaller, more manageable steps. Compare two decimals at a time and then combine the results to order the entire set.
5.4 Double-Check Your Work
Always double-check your work to ensure that you have not made any mistakes. Pay close attention to the place value of each digit and make sure you are comparing like with like.
5.5 Understand Common Decimal Equivalents
Familiarize yourself with common decimal equivalents for fractions, such as 0.5 for 1/2, 0.25 for 1/4, and 0.75 for 3/4. This knowledge can help you quickly compare decimals and fractions.
6. Common Mistakes to Avoid
When comparing and ordering decimals, it’s easy to make mistakes. Here are some common pitfalls to watch out for:
6.1 Ignoring Place Value
One of the most common mistakes is ignoring place value. Always make sure you are comparing digits in the same place value (tenths with tenths, hundredths with hundredths, etc.).
6.2 Not Aligning Decimal Points
Failing to align the decimal points can lead to incorrect comparisons. Make sure the decimal points are aligned vertically before comparing the digits.
6.3 Assuming Longer Decimals are Always Larger
A longer decimal (with more digits) is not always larger. For example, 0.1 is greater than 0.099, even though 0.099 has more digits.
6.4 Forgetting to Add Placeholders
When comparing decimals with different numbers of digits, forgetting to add zeros as placeholders can lead to errors. Always add zeros to make the lengths of the decimals equal before comparing.
6.5 Overlooking the Whole Number Part
Always compare the whole number part first. If the whole numbers are different, the decimal with the larger whole number is greater, regardless of the digits after the decimal point.
7. Practice Problems and Solutions
To solidify your understanding, let’s work through some practice problems:
Problem 1:
Order the following decimals in ascending order: 0.45, 0.6, 0.32, 0.5.
Solution:
- Compare 0.45 and 0.6: 0.45 < 0.6
- Compare 0.45 and 0.32: 0.32 < 0.45
- Compare 0.45 and 0.5: 0.45 < 0.5
Arranging in ascending order: 0.32, 0.45, 0.5, 0.6.
Problem 2:
Order the following decimals in descending order: 1.8, 1.75, 1.92, 1.7.
Solution:
- Compare 1.8 and 1.75: 1.8 > 1.75
- Compare 1.8 and 1.92: 1.92 > 1.8
- Compare 1.8 and 1.7: 1.8 > 1.7
Arranging in descending order: 1.92, 1.8, 1.75, 1.7.
Problem 3:
Which is greater: 2.35 or 2.345?
Solution:
- Compare 2.35 and 2.345:
- Whole number part is the same (2).
- Tenths place is the same (3).
- Hundredths place: 5 > 4.
Therefore, 2.35 > 2.345.
Problem 4:
Arrange the following decimals from least to greatest: 5.05, 5.5, 5.005, 5.55.
Solution:
- Compare 5.05, 5.5, 5.005, 5.55:
- Whole number part is the same (5).
- Compare the tenths place: 0, 5, 0, 5.
- Order the decimals with 0 in the tenths place: 5.05 and 5.005. Comparing hundredths, 5.005 < 5.05.
- Order the decimals with 5 in the tenths place: 5.5 and 5.55. Comparing hundredths, 5.5 < 5.55.
Arranging in ascending order: 5.005, 5.05, 5.5, 5.55.
8. Advanced Techniques for Decimal Comparison
For those looking to deepen their understanding, here are some advanced techniques for decimal comparison:
8.1 Converting Decimals to Fractions
Converting decimals to fractions can sometimes make it easier to compare them, especially if the decimals have repeating patterns.
Example:
Compare 0.333… and 0.25.
Convert 0.333… to 1/3 and 0.25 to 1/4.
Now compare 1/3 and 1/4. Since 1/3 > 1/4, then 0.333… > 0.25.
8.2 Using Benchmarks
Using benchmarks like 0, 0.5, and 1 can help you quickly estimate the relative size of decimals and make comparisons.
Example:
Compare 0.75 and 0.4.
0.75 is closer to 1, while 0.4 is closer to 0.5. Therefore, 0.75 > 0.4.
8.3 Scientific Notation
For very large or very small decimals, using scientific notation can simplify the comparison process.
Example:
Compare 3.2 x 10^-5 and 2.8 x 10^-5.
Since both numbers have the same exponent, compare the decimal parts: 3.2 > 2.8, so 3.2 x 10^-5 > 2.8 x 10^-5.
9. How COMPARE.EDU.VN Can Help You Master Decimals
At COMPARE.EDU.VN, we understand the challenges students and professionals face when dealing with decimals. That’s why we’ve created a suite of resources designed to help you master decimal comparison and ordering. Our comprehensive guides, interactive tools, and practice problems provide you with the knowledge and skills you need to succeed.
9.1 Detailed Comparison Guides
Our detailed comparison guides break down the process of comparing decimals into simple, easy-to-follow steps. We provide clear explanations, real-world examples, and helpful tips to ensure that you understand the concepts thoroughly.
9.2 Interactive Tools
Our interactive tools allow you to practice comparing decimals in a fun and engaging way. You can use our number line tool to visualize decimals and our place value chart to understand the value of each digit.
9.3 Practice Problems and Quizzes
We offer a wide range of practice problems and quizzes to test your knowledge and reinforce your skills. Our problems cover various difficulty levels, allowing you to gradually increase your proficiency.
9.4 Expert Insights
Our team of math experts provides valuable insights and strategies for mastering decimals. We share common mistakes to avoid, advanced techniques for complex comparisons, and tips for applying your knowledge in real-world scenarios.
9.5 Personalized Learning Experience
At COMPARE.EDU.VN, we believe in personalized learning. Our platform adapts to your individual needs, providing you with customized resources and support to help you achieve your goals.
10. Conclusion: Making Informed Decisions with Decimals
Comparing and ordering decimals is a fundamental skill with wide-ranging applications. Whether you’re shopping for the best deals, cooking a recipe, analyzing sports statistics, or conducting scientific experiments, the ability to accurately compare decimals is essential.
By understanding the principles of place value, following a step-by-step comparison process, and practicing regularly, you can master this skill and make informed decisions in all aspects of your life.
Don’t let the complexities of decimals hold you back. Visit COMPARE.EDU.VN today and discover how our comprehensive resources can help you master decimal comparison and ordering. Our detailed guides, interactive tools, and expert insights will empower you to tackle any numerical challenge with confidence.
Ready to make smarter decisions with decimals? Explore COMPARE.EDU.VN now and unlock your full potential! For further assistance, visit us at 333 Comparison Plaza, Choice City, CA 90210, United States, or contact us via Whatsapp at +1 (626) 555-9090. Let COMPARE.EDU.VN be your trusted partner in mastering decimals and making informed choices.
11. FAQs About Comparing and Ordering Decimals
11.1 What is a decimal?
A decimal is a number that includes a whole number part and a fractional part, separated by a decimal point.
11.2 Why is it important to align decimal points when comparing decimals?
Aligning decimal points ensures that you are comparing digits in the same place value, which is crucial for accurate comparisons.
11.3 How do you add placeholders when comparing decimals?
Add zeros to the right of the last digit after the decimal point to make the lengths of the decimals equal. This does not change the value of the decimal but ensures that you are comparing digits in the same place value.
11.4 What is ascending order?
Ascending order means arranging numbers from the smallest to the largest.
11.5 What is descending order?
Descending order means arranging numbers from the largest to the smallest.
11.6 What is the most common mistake when comparing decimals?
The most common mistake is ignoring place value and not comparing digits in the same place value.
11.7 Can you always assume that a longer decimal is larger?
No, a longer decimal (with more digits) is not always larger. Always compare the digits in the same place value to determine which decimal is greater.
11.8 How can a number line help in comparing decimals?
A number line provides a visual representation of decimals, making it easier to see which decimal is larger or smaller. The decimal further to the right on the number line is the larger number.
11.9 How can I improve my decimal comparison skills?
Practice regularly, use visual aids like number lines and place value charts, break down complex problems into smaller steps, and double-check your work.
11.10 Where can I find more resources for learning about decimals?
Visit compare.edu.vn for comprehensive guides, interactive tools, and practice problems designed to help you master decimal comparison and ordering.