Comparing fractions can be straightforward with the right methods. This guide, brought to you by COMPARE.EDU.VN, offers a comprehensive overview of various techniques to compare fractions, from those with common denominators to those requiring a bit more calculation, enabling you to easily determine which fraction is larger or smaller. Explore different fraction comparison methods and enhance your number sense to navigate mathematical challenges effectively and utilize tools to simplify fractions!
1. Understanding Fraction Comparison
How Do We Compare Fractions to determine their relative size?
Comparing fractions involves determining which fraction represents a larger or smaller portion of a whole. This is essential in various real-life situations, from cooking and baking to understanding financial ratios and proportions. Comparing fractions means assessing their values to establish if one fraction is less than, greater than, or equal to another. Understanding how to compare fractions is a fundamental skill in mathematics with broad applications.
1.1 What is a Fraction?
What are the key components of a fraction?
A fraction represents a part of a whole and is expressed as a numerator over a denominator. The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. Understanding the numerator and denominator is fundamental to comparing fractions. For instance, in the fraction 3/4, 3 is the numerator, and 4 is the denominator, indicating that we have 3 parts out of a total of 4.
1.2 Why is Fraction Comparison Important?
Why is it important to learn how to compare fractions effectively?
Comparing fractions is a fundamental skill with applications in everyday life. Whether you’re adjusting recipe quantities, managing finances, or analyzing data, understanding how to compare fractions is essential for making informed decisions. This skill also builds a strong foundation for more advanced mathematical concepts, such as algebra and calculus. Understanding relative sizes allows for accurate and efficient problem-solving across various domains.
2. Comparing Fractions with the Same Denominators
How do you compare fractions when they share a common denominator?
When comparing fractions with the same denominators, the fraction with the larger numerator is the larger fraction. This is because both fractions represent parts of the same whole, divided into the same number of equal parts. Therefore, the fraction with more of those parts is the greater one. Comparing fractions with the same denominators is one of the simplest methods of comparison.
2.1 Step-by-Step Guide
How can you quickly compare fractions with identical denominators?
- Check the Denominators: Ensure that the denominators of both fractions are the same.
- Compare the Numerators: Identify the larger numerator.
- Determine the Larger Fraction: The fraction with the larger numerator is the larger fraction.
For example, when comparing 3/7 and 5/7, since 5 > 3, we know that 5/7 is the larger fraction.
2.2 Examples of Comparing Fractions with Same Denominators
Can you provide some practical examples of how to compare fractions with the same denominators?
Example 1:
Compare 2/9 and 7/9.
- Both fractions have the same denominator (9).
- Compare the numerators: 2 and 7.
- Since 7 > 2, then 7/9 > 2/9.
Example 2:
Compare 11/15 and 8/15.
- Both fractions have the same denominator (15).
- Compare the numerators: 11 and 8.
- Since 11 > 8, then 11/15 > 8/15.
3. Comparing Fractions with Unlike Denominators
What are the methods for comparing fractions that have different denominators?
Comparing fractions with unlike denominators requires converting the fractions to have a common denominator before comparing their numerators. This ensures that both fractions are representing parts of the same whole, making the comparison accurate. Methods include finding the Least Common Multiple (LCM) or using cross-multiplication. These strategies simplify the process of comparing fractions with unlike denominators.
3.1 Finding the Least Common Multiple (LCM)
How does finding the LCM help in comparing fractions with different denominators?
Finding the Least Common Multiple (LCM) of the denominators allows you to convert fractions into equivalent fractions with a common denominator. Once the denominators are the same, you can easily compare the numerators to determine which fraction is larger. This method ensures an accurate comparison between fractions with unlike denominators.
3.1.1 Step-by-Step Guide to Using LCM
What steps should you follow to compare fractions using the LCM method?
- Find the LCM: Determine the Least Common Multiple (LCM) of the denominators.
- Convert Fractions: Convert each fraction into an equivalent fraction with the LCM as the new denominator.
- Compare Numerators: Compare the numerators of the new fractions. The fraction with the larger numerator is the larger fraction.
For instance, to compare 1/3 and 2/5:
- The LCM of 3 and 5 is 15.
- Convert 1/3 to 5/15 (multiply numerator and denominator by 5).
- Convert 2/5 to 6/15 (multiply numerator and denominator by 3).
- Since 6/15 > 5/15, then 2/5 > 1/3.
3.1.2 Examples Using LCM
Can you provide examples to illustrate how to compare fractions using the LCM?
Example 1:
Compare 3/4 and 5/6.
- The LCM of 4 and 6 is 12.
- Convert 3/4 to 9/12 (multiply numerator and denominator by 3).
- Convert 5/6 to 10/12 (multiply numerator and denominator by 2).
- Since 10/12 > 9/12, then 5/6 > 3/4.
Example 2:
Compare 2/3 and 4/7.
- The LCM of 3 and 7 is 21.
- Convert 2/3 to 14/21 (multiply numerator and denominator by 7).
- Convert 4/7 to 12/21 (multiply numerator and denominator by 3).
- Since 14/21 > 12/21, then 2/3 > 4/7.
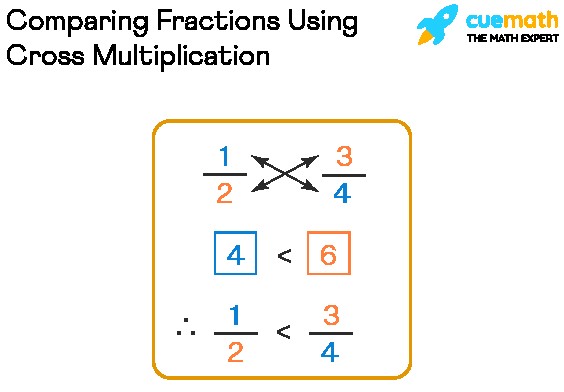
3.2 Cross-Multiplication Method
What is the cross-multiplication method, and how is it used to compare fractions?
The cross-multiplication method involves multiplying the numerator of one fraction by the denominator of the other fraction and comparing the results. This method quickly determines which fraction is larger without explicitly finding a common denominator. It’s a useful shortcut for comparing two fractions.
3.2.1 Step-by-Step Guide to Cross-Multiplication
How can you apply the cross-multiplication method to determine the larger fraction?
- Cross Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction.
- Cross Multiply Again: Multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the Products: Compare the two products. The fraction corresponding to the larger product is the larger fraction.
For instance, to compare 2/5 and 3/7:
- Multiply 2 (numerator of the first fraction) by 7 (denominator of the second fraction) to get 14.
- Multiply 3 (numerator of the second fraction) by 5 (denominator of the first fraction) to get 15.
- Since 15 > 14, then 3/7 > 2/5.
3.2.2 Examples Using Cross-Multiplication
Can you demonstrate the cross-multiplication method with a couple of examples?
Example 1:
Compare 4/9 and 5/11.
- Multiply 4 by 11 to get 44.
- Multiply 5 by 9 to get 45.
- Since 45 > 44, then 5/11 > 4/9.
Example 2:
Compare 1/4 and 2/9.
- Multiply 1 by 9 to get 9.
- Multiply 2 by 4 to get 8.
- Since 9 > 8, then 1/4 > 2/9.
3.3 Comparing Fractions with the Same Numerator
What happens when you need to compare fractions with identical numerators but different denominators?
When comparing fractions with the same numerator, the fraction with the smaller denominator is the larger fraction. This is because if you divide a whole into fewer parts, each part will be larger. This principle simplifies the comparison process when numerators are identical.
3.3.1 How to Compare Fractions with the Same Numerator
How can you quickly determine which fraction is larger when they have the same numerator?
- Identify the Numerators: Confirm that the numerators are the same.
- Compare the Denominators: Identify the smaller denominator.
- Determine the Larger Fraction: The fraction with the smaller denominator is the larger fraction.
For example, when comparing 3/5 and 3/8, since 5 < 8, we know that 3/5 is the larger fraction.
3.3.2 Examples Comparing Fractions with the Same Numerator
Can you show a few examples of how to compare fractions with identical numerators?
Example 1:
Compare 5/7 and 5/11.
- Both fractions have the same numerator (5).
- Compare the denominators: 7 and 11.
- Since 7 < 11, then 5/7 > 5/11.
Example 2:
Compare 2/3 and 2/5.
- Both fractions have the same numerator (2).
- Compare the denominators: 3 and 5.
- Since 3 < 5, then 2/3 > 2/5.
4. Decimal Method of Comparing Fractions
How can converting fractions to decimals help in comparing their values?
Converting fractions to decimals allows for a straightforward comparison by expressing each fraction as a decimal number. This method is particularly useful when dealing with fractions that have unlike denominators or when needing to compare multiple fractions at once. The fraction with the larger decimal value is the larger fraction.
4.1 Converting Fractions to Decimals
What is the process of converting a fraction into its decimal equivalent?
To convert a fraction to a decimal, divide the numerator by the denominator. The resulting decimal is the decimal equivalent of the fraction. This process is straightforward and allows for easy comparison.
For instance, to convert 3/4 to a decimal:
- Divide 3 by 4.
- The result is 0.75.
- Therefore, the decimal equivalent of 3/4 is 0.75.
4.2 Comparing Decimals
How do you compare decimal numbers to determine which fraction is larger?
Comparing decimals involves examining the digits from left to right. Start by comparing the whole number part. If they are the same, compare the tenths place, then the hundredths place, and so on until you find a difference. The decimal with the larger digit in the first differing place is the larger decimal. This method allows for precise comparison of fractions.
For example, compare 0.65 and 0.72:
- The whole number part is 0 in both cases.
- Compare the tenths place: 7 > 6.
- Therefore, 0.72 > 0.65.
4.3 Examples of Comparing Fractions Using Decimals
Can you provide examples of how to compare fractions by converting them to decimals?
Example 1:
Compare 1/5 and 1/4.
- Convert 1/5 to a decimal: 1 ÷ 5 = 0.2.
- Convert 1/4 to a decimal: 1 ÷ 4 = 0.25.
- Since 0.25 > 0.2, then 1/4 > 1/5.
Example 2:
Compare 3/8 and 4/10.
- Convert 3/8 to a decimal: 3 ÷ 8 = 0.375.
- Convert 4/10 to a decimal: 4 ÷ 10 = 0.4.
- Since 0.4 > 0.375, then 4/10 > 3/8.
5. Comparing Fractions Using Visualization
How can visual models aid in comparing fractions?
Visual models, such as pie charts, bar diagrams, and number lines, can provide a clear and intuitive way to compare fractions. These models help represent fractions as parts of a whole, making it easier to see which fraction represents a larger portion. Visual comparison is especially useful for learners who benefit from visual aids.
5.1 Using Pie Charts
How do pie charts visually represent fractions for comparison?
Pie charts represent fractions as slices of a circle, where each slice corresponds to a fraction of the whole. By visually comparing the sizes of the slices, you can easily determine which fraction is larger. Pie charts offer a clear and immediate visual comparison.
To use pie charts:
- Draw two identical pie charts.
- Divide each pie chart into the number of parts indicated by the denominator of each fraction.
- Shade the number of parts indicated by the numerator of each fraction.
- Compare the shaded areas to determine which fraction is larger.
5.2 Using Bar Diagrams
How do bar diagrams facilitate the comparison of fractions?
Bar diagrams use rectangular bars to represent fractions, where the length of the bar corresponds to the fraction’s value. By placing the bar diagrams side by side, you can visually compare the lengths of the bars to determine which fraction is larger. Bar diagrams offer a direct and simple visual comparison.
To use bar diagrams:
- Draw two identical rectangles.
- Divide each rectangle into the number of parts indicated by the denominator of each fraction.
- Shade the number of parts indicated by the numerator of each fraction.
- Compare the lengths of the shaded areas to determine which fraction is larger.
5.3 Using Number Lines
How can number lines be used to compare fractions visually?
Number lines provide a linear representation of fractions, allowing you to plot each fraction on the line and visually compare their positions. The fraction located farther to the right on the number line is the larger fraction. Number lines are particularly useful for illustrating the relative values of multiple fractions.
To use number lines:
- Draw a number line from 0 to 1.
- Divide the number line into equal parts based on the denominators of the fractions.
- Plot each fraction on the number line.
- Compare the positions of the fractions to determine which fraction is larger.
5.4 Examples of Comparing Fractions Using Visualization
Can you provide visual examples of comparing fractions using pie charts, bar diagrams, and number lines?
Example 1:
Compare 1/3 and 1/2 using visual methods.
- Pie Charts: Draw two identical pie charts. Divide one into three parts and shade one part (1/3). Divide the other into two parts and shade one part (1/2). Visually, the shaded area for 1/2 is larger.
- Bar Diagrams: Draw two identical rectangles. Divide one into three parts and shade one part (1/3). Divide the other into two parts and shade one part (1/2). Visually, the shaded length for 1/2 is longer.
- Number Lines: Draw a number line from 0 to 1. Divide the line into segments representing fractions with denominators 3 and 2. Plot 1/3 and 1/2. Visually, 1/2 is farther to the right.
Example 2:
Compare 2/5 and 3/4 using visual models.
- Pie Charts: Draw two identical pie charts. Divide one into five parts and shade two parts (2/5). Divide the other into four parts and shade three parts (3/4). Visually, the shaded area for 3/4 is larger.
- Bar Diagrams: Draw two identical rectangles. Divide one into five parts and shade two parts (2/5). Divide the other into four parts and shade three parts (3/4). Visually, the shaded length for 3/4 is longer.
- Number Lines: Draw a number line from 0 to 1. Divide the line into segments representing fractions with denominators 5 and 4. Plot 2/5 and 3/4. Visually, 3/4 is farther to the right.
6. Tips and Tricks for Comparing Fractions
What are some helpful strategies to simplify fraction comparison?
Simplifying fractions, using benchmarks, and understanding the relationship between numerators and denominators can make comparing fractions easier. These strategies provide quick ways to estimate and compare fractions efficiently. Using benchmarks allows you to quickly assess whether a fraction is close to 0, 1/2, or 1, providing a basis for comparison.
6.1 Simplifying Fractions Before Comparing
How does simplifying fractions make the comparison process easier?
Simplifying fractions to their lowest terms reduces the size of the numbers involved, making it easier to find a common denominator or use cross-multiplication. Simplified fractions are easier to work with and provide a clearer understanding of the fraction’s value. This can streamline the comparison process and reduce errors.
For example, compare 4/8 and 2/3:
- Simplify 4/8 to 1/2.
- Now compare 1/2 and 2/3.
- This simplified comparison is easier to handle.
6.2 Using Benchmark Fractions
How can benchmark fractions like 0, 1/2, and 1 help in comparing fractions?
Benchmark fractions (0, 1/2, and 1) provide a reference point for estimating and comparing fractions. By determining whether a fraction is closer to 0, 1/2, or 1, you can quickly assess its relative size and compare it to other fractions. This method is useful for quick estimations and mental math.
To use benchmark fractions:
- Determine if each fraction is closer to 0, 1/2, or 1.
- Compare their positions relative to the benchmarks.
- Make a comparison based on their proximity to the benchmarks.
For instance, compare 2/5 and 7/8:
- 2/5 is slightly less than 1/2.
- 7/8 is close to 1.
- Therefore, 7/8 is larger than 2/5.
6.3 Understanding Numerator and Denominator Relationships
How does understanding the relationship between the numerator and denominator aid in fraction comparison?
Understanding the relationship between the numerator and denominator helps in making quick comparisons. For example, if the numerator is much smaller than the denominator, the fraction is close to 0. If the numerator is close to the denominator, the fraction is close to 1. This understanding can help you estimate the value of fractions and compare them more easily.
Consider the following:
- If the numerator is half the denominator, the fraction equals 1/2.
- If the numerator is more than half the denominator, the fraction is greater than 1/2.
- If the numerator is less than half the denominator, the fraction is less than 1/2.
For instance, compare 3/7 and 5/8:
- In 3/7, 3 is less than half of 7, so it’s less than 1/2.
- In 5/8, 5 is more than half of 8, so it’s more than 1/2.
- Therefore, 5/8 > 3/7.
7. Real-World Applications of Comparing Fractions
In what real-life scenarios is the ability to compare fractions useful?
Comparing fractions is essential in numerous real-life situations, including cooking, finance, construction, and academics. From adjusting recipe quantities to understanding financial data, the ability to compare fractions allows for informed decision-making and problem-solving in everyday contexts. These skills are critical for both personal and professional success.
7.1 Cooking and Baking
How is comparing fractions used in cooking and baking?
In cooking and baking, recipes often require adjusting ingredient quantities. Comparing fractions allows you to scale recipes up or down while maintaining the correct proportions. For example, if a recipe calls for 1/2 cup of flour and you want to double the recipe, you need to know that doubling 1/2 results in 1 cup. Understanding fraction comparison ensures accurate measurements and consistent results.
7.2 Financial Planning
How does comparing fractions aid in financial planning and budgeting?
In financial planning, comparing fractions is useful for understanding proportions and ratios. For example, comparing the fraction of your income spent on housing versus other expenses can help you create a budget and make informed financial decisions. Knowing how to compare these fractions provides insights into your spending habits and helps you allocate resources effectively.
7.3 Construction and Measurement
How is comparing fractions relevant in construction and measurement tasks?
In construction, accurate measurements are essential. Comparing fractions of an inch or a meter ensures that materials are cut to the correct size. For example, if you need to cut a piece of wood that is 3/4 of an inch shorter than another piece, you need to compare fractions to ensure precision. Accurate measurements lead to structurally sound and aesthetically pleasing results.
7.4 Academic Studies
How is comparing fractions used in various academic subjects?
In academic studies, comparing fractions is crucial for subjects like math, science, and engineering. Whether you’re calculating probabilities, understanding ratios, or analyzing data, comparing fractions is a fundamental skill. For example, in physics, you might need to compare fractions of energy or momentum. In chemistry, you might compare molar ratios. In mathematics, fractions show up in nearly every calculation. A solid grasp of fraction comparison enhances comprehension and problem-solving abilities across multiple disciplines.
8. Common Mistakes to Avoid When Comparing Fractions
What are some typical errors made when comparing fractions, and how can you avoid them?
Common mistakes when comparing fractions include neglecting to find a common denominator, incorrectly applying the cross-multiplication method, or misunderstanding the relationship between numerators and denominators. Recognizing these pitfalls and understanding how to correct them is essential for accurate and efficient fraction comparison. Addressing these mistakes ensures confidence in your mathematical skills.
8.1 Forgetting to Find a Common Denominator
Why is it crucial to find a common denominator before comparing fractions?
Forgetting to find a common denominator when comparing fractions with unlike denominators is a common mistake. Without a common denominator, you are not comparing equal parts of the same whole, leading to inaccurate comparisons. Always ensure that fractions have the same denominator before comparing their numerators.
To avoid this mistake:
- Check if the denominators are the same.
- If not, find the Least Common Multiple (LCM) of the denominators.
- Convert the fractions to equivalent fractions with the LCM as the denominator.
- Compare the numerators.
8.2 Misapplying Cross-Multiplication
How can you correctly apply the cross-multiplication method to avoid errors?
Misapplying cross-multiplication can lead to incorrect comparisons. A common mistake is not multiplying the correct numerators and denominators or comparing the products in the wrong order. Understanding the correct steps and practicing the method can prevent these errors.
To correctly apply cross-multiplication:
- Multiply the numerator of the first fraction by the denominator of the second fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the products. The fraction corresponding to the larger product is the larger fraction.
8.3 Misunderstanding Numerator and Denominator Relationships
How can a misunderstanding of numerator and denominator relationships lead to errors?
Misunderstanding the relationship between numerators and denominators can lead to incorrect assumptions about the size of fractions. For example, assuming that a larger denominator always means a larger fraction (without considering the numerator) is a common error. Understanding how numerators and denominators relate to the overall value of a fraction is crucial for accurate comparisons.
To avoid this mistake:
- Remember that when numerators are the same, the fraction with the smaller denominator is larger.
- Understand that when denominators are the same, the fraction with the larger numerator is larger.
- Use benchmarks like 0, 1/2, and 1 to estimate the value of fractions.
9. Practice Problems
9.1 Fraction Comparison Problems
- Compare 2/5 and 3/8.
- Which is larger: 4/7 or 5/9?
- Compare 1/3, 2/5, and 3/7.
- Arrange the following fractions in ascending order: 3/4, 5/8, 1/2.
- Determine which fraction is closest to 1/2: 3/5, 4/9, or 5/11.
9.2 Solutions
- Compare 2/5 and 3/8:
- Using cross-multiplication: 2 8 = 16, 3 5 = 15.
- Since 16 > 15, 2/5 > 3/8.
- Which is larger: 4/7 or 5/9?
- Using cross-multiplication: 4 9 = 36, 5 7 = 35.
- Since 36 > 35, 4/7 > 5/9.
- Compare 1/3, 2/5, and 3/7:
- Find the LCM of 3, 5, and 7: LCM = 105.
- Convert fractions: 1/3 = 35/105, 2/5 = 42/105, 3/7 = 45/105.
- Comparing numerators: 35 < 42 < 45.
- Therefore, 1/3 < 2/5 < 3/7.
- Arrange the following fractions in ascending order: 3/4, 5/8, 1/2.
- Find the LCM of 4, 8, and 2: LCM = 8.
- Convert fractions: 3/4 = 6/8, 5/8 = 5/8, 1/2 = 4/8.
- Comparing numerators: 4 < 5 < 6.
- Therefore, 1/2 < 5/8 < 3/4.
- Determine which fraction is closest to 1/2: 3/5, 4/9, or 5/11.
- Convert fractions to decimals: 3/5 = 0.6, 4/9 ≈ 0.44, 5/11 ≈ 0.45.
- Decimal equivalent of 1/2 = 0.5.
- Comparing decimals to 0.5: |0.6 – 0.5| = 0.1, |0.44 – 0.5| = 0.06, |0.45 – 0.5| = 0.05.
- Since 0.05 is the smallest difference, 5/11 is closest to 1/2.
10. Conclusion
Mastering the art of comparing fractions involves understanding various methods and strategies to determine their relative values. From comparing fractions with common denominators to using LCM, cross-multiplication, decimal conversion, and visual models, each technique offers a unique way to approach fraction comparison. By understanding and practicing these methods, you can confidently tackle any fraction comparison problem that comes your way. This skill is invaluable in various real-life scenarios and academic pursuits.
Do you find yourself struggling to compare complex fractions? Visit COMPARE.EDU.VN today for more in-depth guides and tools to help you master fraction comparison and make informed decisions in your daily life! Our resources are designed to simplify complex concepts and provide you with the confidence you need.
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
Whatsapp: +1 (626) 555-9090
Website: compare.edu.vn
11. FAQs on Comparing Fractions
11.1 What does it mean to compare fractions?
Comparing fractions means determining whether one fraction is greater than, less than, or equal to another fraction. This involves understanding the relative values of the fractions and their positions on a number line.
11.2 How do you compare fractions with the same denominator?
When fractions have the same denominator, you simply compare the numerators. The fraction with the larger numerator is the larger fraction. For example, 5/7 > 3/7 because 5 is greater than 3.
11.3 What is the easiest way to compare fractions?
The easiest way to compare fractions depends on the given fractions. If they have the same denominator, compare the numerators. If they have different denominators, consider using cross-multiplication or converting the fractions to decimals.
11.4 How do you compare fractions with different denominators?
To compare fractions with different denominators, you first need to find a common denominator. Once you have a common denominator, you can compare the numerators to determine which fraction is larger.
11.5 Can you compare fractions with negative numbers?
Yes, you can compare fractions with negative numbers. Remember that negative numbers are always less than positive numbers. When comparing two negative fractions, the one with the smaller absolute value is larger.
11.6 Why is it important to know how to compare fractions?
Knowing how to compare fractions is essential for various real-life applications, including cooking, baking, financial planning, construction, and academics. It allows you to make informed decisions and solve problems accurately.
11.7 How can visual aids help in comparing fractions?
Visual aids such as pie charts, bar diagrams, and number lines can help you visualize the relative sizes of fractions. These models make it easier to compare fractions and understand their values intuitively.
11.8 What is a benchmark fraction, and how can it help?
A benchmark fraction is a common fraction such as 0, 1/2, or 1 that can be used as a reference point for estimating and comparing other fractions. Determining whether a fraction is closer to 0, 1/2, or 1 can help you quickly assess its relative size.
11.9 What are some common mistakes to avoid when comparing fractions?
Common mistakes include forgetting to find a common denominator, misapplying cross-multiplication, and misunderstanding the relationship between numerators and denominators. Being aware of these mistakes can help you avoid them.
11.10 How do you convert a fraction to a decimal?
To convert a fraction to a decimal, divide the numerator by the denominator. The resulting decimal is the decimal equivalent of the fraction. This allows for easy comparison of fractions.